Practice Problems

STAT 205: Introduction to Mathematical Statistics

Author

Affiliation

Dr. Irene Vrbik

University of British Columbia Okanagan

1 Data

Quarto

Exercise 1.1 What is the extension for quarto documents?

1. .rmd
2. .qmd
3. .html
4. .r
5. .qrt

Solution

qmd

Exercise 1.2 What does echo: false do in a Quarto code chunk?

1. Hides both the code and its output
   
2. Displays the code but hides the output
   
3. Displays the output but hides the code
   
4. Runs the code but does not execute it
   

Solution

3. Displays the output but hides the code

Exercise 1.3 Which of the following is NOT part of the YAML section in a Quarto document?

1. title
2. author
3. output
4. subtitle

Solution

output See here for a complete list of options for the HTML format and here for a brief description of a YAML

Exercise 1.4 What is the syntax for producing code chunks in Quarto?

1. Use single backticks with r inside
2. Use triple backticks with {r} at the start:
3. Use single backticks with {r} inside
4. Use triple backticks with {.r} at the start:

Solution

Use triple backticks with {r} at the start:

Exercise 1.5 What does echo: false do in a Quarto code chunk?

1. Hides both the code and its output
2. Displays the code but hides the output
3. Displays the output but hides the code
4. Runs the code but does not execute it

Solution

Displays the output but hides the code

Exercise 1.6 Why is setting a seed important in R, and how do you set one?

Solution

Setting a seed ensures reproducibility by making random number generation consistent across runs. In R, you set a seed using set.seed(number), where number is any fixed integer (e.g., set.seed(123)).

Data Types

Exercise 1.7 Based on the output below, identify which data type x has been coded as.

x <- factor(c("A", "B", "C", "A"),
        levels = c("A", "B", "C")) 
x

1. numeric
   
2. integer
   
3. character
   
4. unordered factor
   
5. ordered factor
   

Solution

4. unordered factor

Exercise 1.8 In the context of variables, which of the following is an example of a categorical variable?

1. Height of individuals.
2. Number of countries visited.
3. Gender of individuals.
4. Hours of sleep per night.

Solution

Gender of individuals.

Data Summaries and Visualization

Exercise 1.9 Which measure of central tendency is defined as the middle value when data is ordered?

1. Mean
   
2. Median
3. Mode
   
4. Range

Solution

Median

Exercise 1.10 The Interquartile Range (IQR) measures:

1. The difference between the maximum and minimum values
   
2. The spread of the middle 50% of the data
   
3. The average deviation from the mean
   
4. The most frequently occurring value

Solution

The spread of the middle 50% of the data

Exercise 1.11 What does the breaks argument in the hist function do?

Solution

The breaks argument in the hist function determines how data is divided into bins. It can be:
- A single number specifying the approximate number of bins.
- A vector specifying exact breakpoints.
- A function that computes breakpoints dynamically.

More bins result in more bars and smaller bin widths.

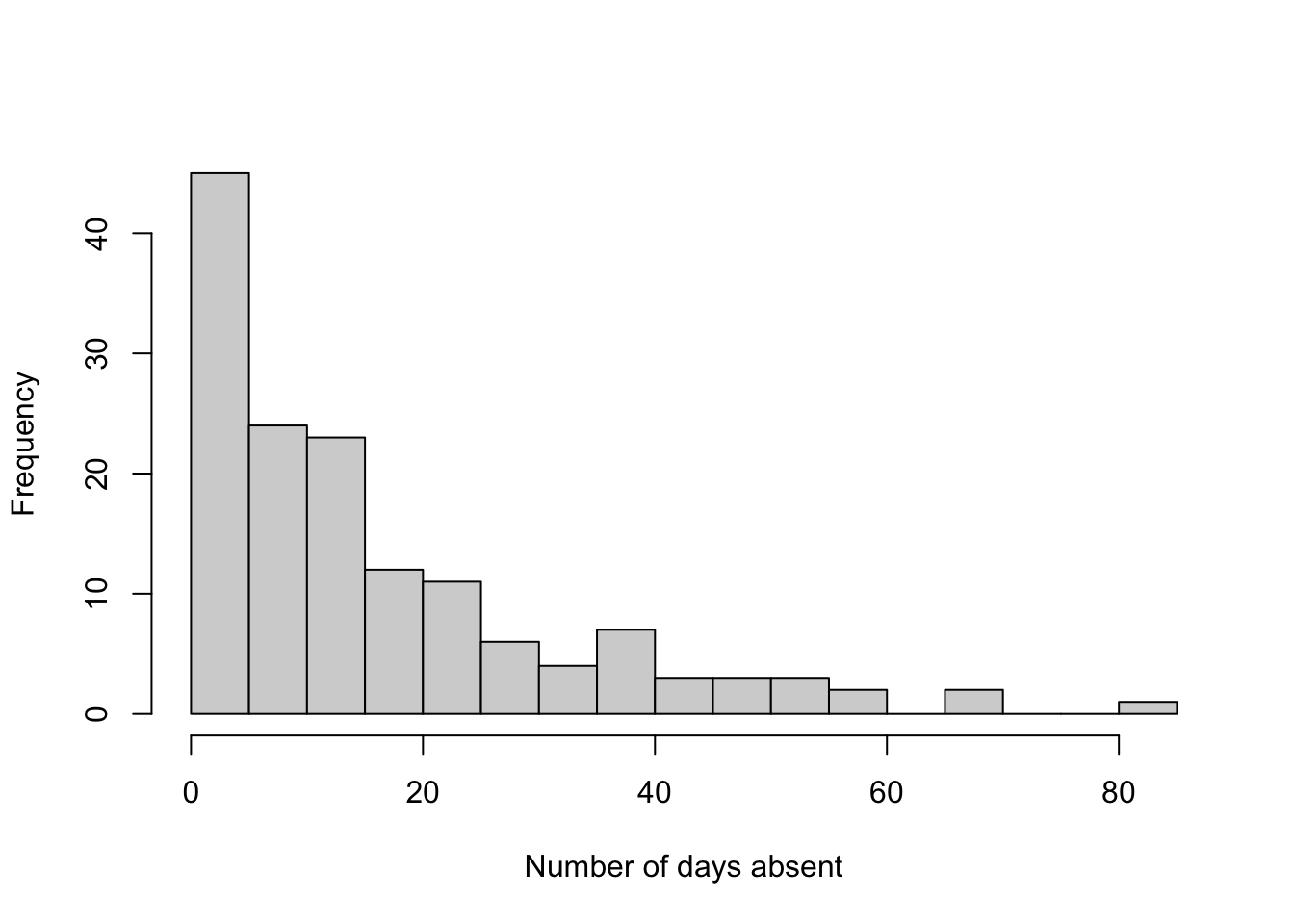
Exercise 1.12 Consider Figure Figure 1.1, estimate the median number of absent days.

1. 5
2. 16.46
3. 11
4. 22.75

Solution

3. Median number of absenteeism days is calculated in R using:

round(median(absenteeism$days),2)

[1] 11

You can estimate it from the boxplot (the median is represented by the horizontal line inside the box of the boxplot).

(a) Histogram of Absenteeism

(b) Boxplot of Absenteeism

Figure 1.1: Absenteeism from school in New South Wales

Data Collection

Exercise 1.13 What is the primary difference between descriptive and inferential statistics?

1. Descriptive statistics involve collecting data, while inferential statistics involve presenting data.
2. Descriptive statistics summarize data; inferential statistics draw conclusions about a population based on a sample.
3. Descriptive statistics are used in experiments; inferential statistics are used in observational studies.
4. Descriptive statistics require large datasets; inferential statistics require small datasets.

Solution

Descriptive statistics summarize data; inferential statistics draw conclusions about a population based on a sample.

Exercise 1.14 In the context of sampling methods, what is a simple random sample?

1. A sample where each member of the population has an equal chance of being selected.
2. A sample that includes only the first 50 members of the population.
3. A sample divided into subgroups based on specific characteristics.
4. A sample where only members with certain traits are selected.

Solution

A sample where each member of the population has an equal chance of being selected.

Exercise 1.15 Explain what selection bias is and provide an example of how it might occur in a research study.

Solution

Selection bias occurs when the sample chosen for a study is not representative of the population, leading to biased results. An example is surveying only individuals who have internet access for an online study, which excludes those without internet access.

Exercise 1.16 Which type of study involves observing individuals or groups and collecting data without intervening or manipulating any aspect of the study participants?

1. Observational study
   
2. Experimental study
   
3. Longitudinal study
   
4. Retrospective study
   

Solution

1. Observational study

Exercise 1.17 Suppose a researcher wants to study the average income of households in Kelowna.

1. Identify the population of interest.
   
2. Provide an example of a biased sample from the population.
   
3. What is the population parameter of interest? State this in words and symbols.
   

Solution

1. All households in Kelowna. 2. Sampling houses only in a rich neighborhood. 3. The population parameter of interest is** \(\mu\), **the average household income in Kelowna.

2 Estimation and Sampling Distributions

Exercise 2.1 Which of the following statements best describes statistics?

1. Descriptive statistics involve analyzing sample data to draw conclusions about a population.
   
2. Descriptive statistics aim to make predictions and inferences about a population based on sample data.
   
3. Descriptive statistics are used to summarize and describe data through measures such as mean and standard deviation.
   
4. Descriptive statistics involve drawing conclusions about a population based on sample data.
   

Solution

3. Descriptive statistics are used to summarize and describe data through measures such as mean and standard deviation.

Exercise 2.2 True or False: Parameters are descriptive measures computed from a sample, while statistics are descriptive measures computed from a population.

Solution

False

It’s the other way around parameters are descriptive measures computed from a population, while statistics are descriptive measures computed from a sample.

Point Estimation

Method of Moments

Exercise 2.3 Let \(X_1,\dots, X_n\) be a random sample from a gamma probability distribution with parameters \(\alpha\) and \(\beta\).
Recall the Probability Density Function (PDF) of the Gamma Distribution:

\[ f(x; \alpha, \beta) = \frac{\beta^\alpha x^{\alpha - 1} e^{-\beta x}}{\Gamma(\alpha)} \]

where \(x > 0\), \(\alpha > 0\) is the shape parameter, \(\beta > 0\) is the rate parameter, and \(\Gamma(\alpha) = \int_0^\infty x^{\alpha - 1} e^{-x} \, dx\) is the gamma function. Find the method of moment (MoM) estimators for the unknown parameters \(\alpha\) and \(\beta\). You may use the results below:

\[\begin{align} \mathbb{E}[X] &= \alpha\beta, & \text{Var}(X) &= \alpha\beta^2 \end{align}\]

Solution

Using the method of moments, we equate the population moments to the sample moments:

Setting the first population moment equal to the first sample moment and solving for \(\beta\): \[ \mathbb{E}[X] = \alpha \beta \approx \bar{X} \] \[ \beta = \frac{\bar{X}}{\alpha} \]

The second moment equation (using variance): \[ \text{Var}(X) = \alpha \beta^2 \approx S^2 \] Substituting \(\beta\): \[ \alpha \left(\frac{\bar{X}}{\alpha}\right)^2 = S^2 \] \[ \frac{\bar{X}^2}{\alpha} = S^2 \] Solving for \(\alpha\): \[ \alpha = \frac{\bar{X}^2}{S^2} \]

Substituting \(\alpha\) into the equation for \(\beta\): \[ \beta = \frac{S^2}{\bar{X}} \]

Thus, the moment estimators are:

\[ \hat{\alpha} = \frac{\bar{X}^2}{S^2}, \quad \hat{\beta} = \frac{S^2}{\bar{X}} \]

Maximum Likelihood Estimation

Sampling Distribution

Exercise 2.4 Which of the following best describes the concept of sampling distribution?

1. The distribution of a population based on a sample of data.
   
2. The distribution of sample statistics computed from multiple samples drawn from the same population.
   
3. The distribution of data points within a single sample.
   
4. The distribution of a sample based on the characteristics of the population.
   

Solution

2. The distribution of sample statistics computed from multiple samples drawn from the same population.

Exercise 2.5 Let \(X_1, \dots, X_n\) be \(N(\mu, \sigma^2)\).

1. If \(\mu\) is unknown and \(\sigma^2 = \sigma_0^2\) is known, find the MLE for \(\mu\).

Solution

The likelihood function is:

\[ L (\mu, \theta) = (2\pi\theta)^{-n/2} \exp \left( -\frac{\sum_{i=1}^{n} (x_i - \mu)^2}{2\theta} \right) \]

Taking the log-likelihood:

\[ \ln L (\mu, \theta) = -\frac{n}{2} \ln (2\pi) - \frac{n}{2} \ln \theta - \frac{\sum_{i=1}^{n} (x_i - \mu)^2}{2\theta} \]

When \(\sigma^2 = \sigma_0^2\) is known, we estimate only \(\mu\). Differentiating the log-likelihood with respect to \(\mu\):

\[ \frac{\partial}{\partial \mu} \ln L (\mu, \sigma_0^2) = \frac{2 \sum_{i=1}^{n} (x_i - \mu)}{2\sigma_0^2} = \frac{\sum_{i=1}^{n} (x_i - \mu)}{\sigma_0^2} \]

Setting the derivative to zero and solving for \(\mu\):

\[ \sum_{i=1}^{n} (x_i - \mu) = 0 \]

\[ \sum_{i=1}^{n} x_i = n\mu \quad \Rightarrow \quad \hat{\mu} = \bar{X} \]

Thus, the MLE estimator for \(\mu\) is:

\[ \hat{\mu} = \bar{X} \]

2. If \(\mu = \mu_0\) is known and \(\sigma^2\) is unknown, find the MLE for \(\sigma^2\).

Solution

When \(\mu = \mu_0\) is known, we estimate only \(\sigma^2\). Differentiating the log-likelihood function with respect to \(\theta\):

\[ \frac{\partial}{\partial \theta} \ln L (\mu_0, \theta) = -\frac{n}{2\theta} + \frac{\sum_{i=1}^{n} (x_i - \mu_0)^2}{2\theta^2} \]

Setting the derivative to zero and solving for \(\theta\):

\[ \hat{\sigma}^2 = \frac{\sum_{i=1}^{n} (X_i - \mu_0)^2}{n} \]

3. Show that the MLE estimator for \(\mu\) is unbiased.

Solution

The MLE estimator for \(\mu\) is \(\hat{\mu} = \bar{X}\).

To check if it is unbiased, we compute its expectation:

\[ \mathbb{E}[\hat{\mu}] = \mathbb{E}[\bar{X}] \]

Since \(\bar{X} = \frac{1}{n} \sum_{i=1}^{n} X_i\), and using the linearity of expectation:

\[ \mathbb{E}[\bar{X}] = \frac{1}{n} \sum_{i=1}^{n} \mathbb{E}[X_i] \]

Since \(\mathbb{E}[X_i] = \mu\) for all \(i\):

\[ \mathbb{E}[\bar{X}] = \frac{1}{n} \times n\mu = \mu \]

Since \(\mathbb{E}[\hat{\mu}] = \mu\), we conclude that \(\hat{\mu}\) is an unbiased estimator of \(\mu\).

Exercise 2.6 Let \(\hat{\theta}_1\) be the sample mean and \(\hat{\theta}_2\) be the sample median. It is known that

\[ \text{Var}(\hat{\theta}_2) = (1.2533)^2 \frac{\sigma^2}{n} \]

Find the efficiency of \(\hat{\theta}_2\) relative to \(\hat{\theta}_1\).

Solution

The relative efficiency is given by:

\[ \text{eff}(\hat{\theta}_1, \hat{\theta}_2) = \frac{\text{Var}(\hat{\theta}_1)}{\text{Var}(\hat{\theta}_2)} \]

Substituting the given variances:

\[ \text{eff}(\hat{\theta}_1, \hat{\theta}_2) = \frac{\frac{\sigma^2}{n}}{(1.2533)^2 \frac{\sigma^2}{n}} \]

Simplifying:

\[ = \frac{\sigma^2/n}{1.57076 \cdot (\sigma^2/n)} = \frac{1}{1.57076} \approx 0.6366 \]

Thus, the relative efficiency of \(\hat{\theta}_2\) (the sample median) relative to \(\hat{\theta}_1\) (the sample mean) is 0.6366.

Sample Mean

Exercise 2.7 Suppose we have a manufacturing process where widgets are produced, and the time it takes for a widget to be completed follows an exponential distribution with a mean time of 4 hours. If thirty-five widgets from this manufacturer are chosen at random:

1. Identify the distribution (name and parameters) of the mean completion time.

Solution

Let \(X_i\) be the time to complete the \(i\)th widget, which follows an exponential distribution:

\[ X_i \sim Exp(\lambda = \frac{1}{4}) \]

By the Central Limit Theorem, the mean completion time \(\bar{X}\) for \(n = 35\) follows a Normal distribution with:

• Mean: \(\mu_{\bar{X}} = 1/0.25\)
  

• Standard Error:
  Since the variance of an exponential distribution \(Exp(\lambda)\) is \(\frac{1}{\lambda^2}\), we compute:

  \[ \sigma_{\bar{X}} = \frac{1/\lambda}{\sqrt{n}} = \frac{4}{\sqrt{35}} \approx 0.6761234 \]

Thus, we have:

\[ \bar{X} \sim \text{Normal}(\mu_{\bar X} = 4, \sigma_{\bar X} = 0.676) \]
or we can keep it in fraction form:

\[ \bar{X} \sim \text{Normal}(\mu_{\bar X} = 4, \sigma_{\bar X} = \frac{4}{\sqrt{35}}) \]

2. Find the probability that the mean failure time exceeds 5 hours.

Solution

We compute:

\[ \Pr(\bar{X} > 5) = \Pr \left( Z > \frac{5 - \mu_{\bar{X}}}{\sigma_{\bar{X}}} \right) \]

Substituting values:

\[ \Pr \left( Z > \frac{5 - 4}{4/\sqrt{35}} \right) \]

\[ = \Pr(Z > 1.4790199) \]

Using standard normal tables:

\[\begin{align*} \Pr(Z > 1.479) &= 1 - \Pr(Z \leq 1.479)\\ &= 1 - \Pr(Z \leq 1.479)\\ &= 1 - 0.9304\\ &\approx 0.0696\\ \end{align*}\]

Thus, the probability that the mean failure time exceeds 5 hours is 0.0696.

A graphical representation is shown below:

Sample Proportion

Sample Variance

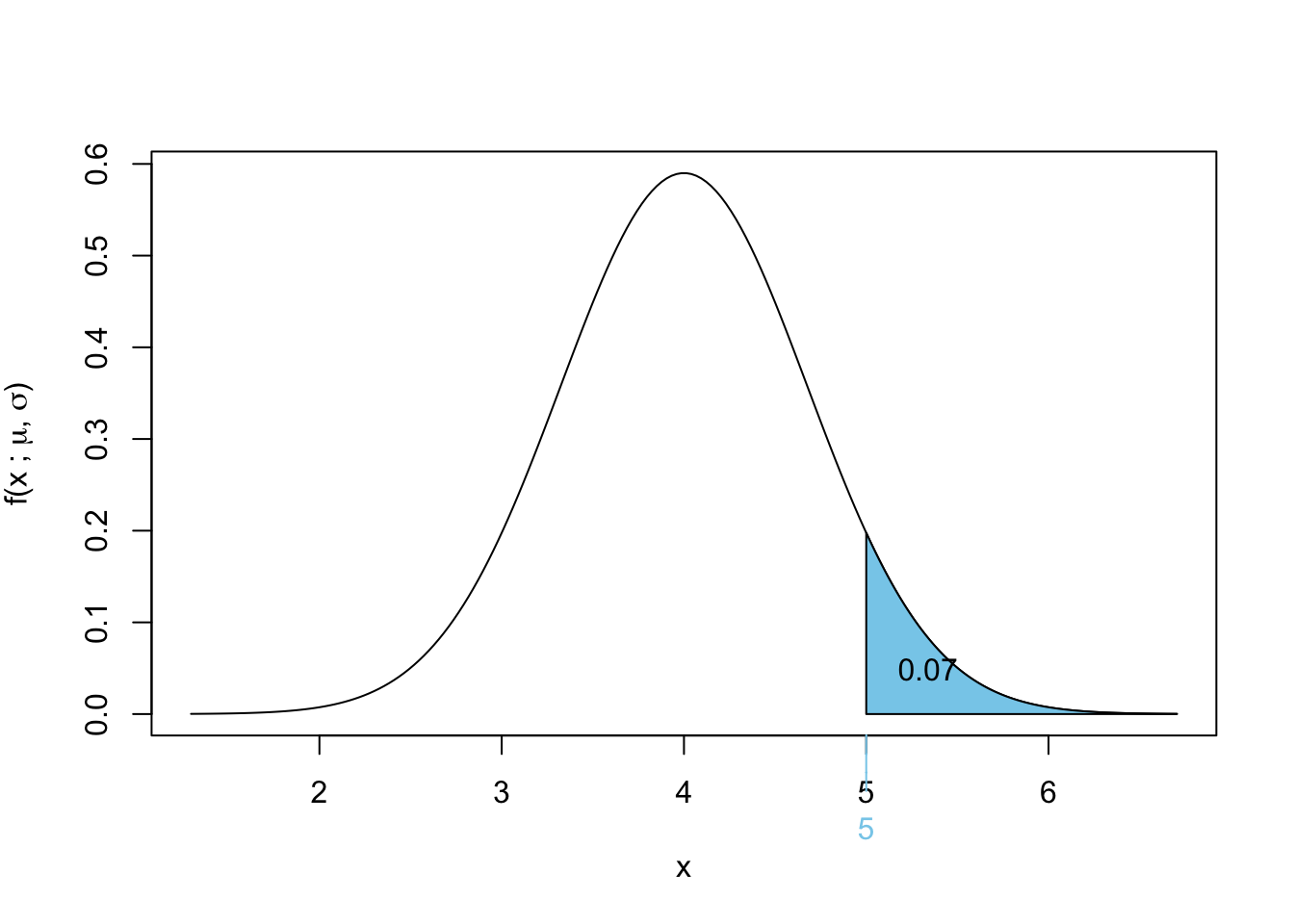
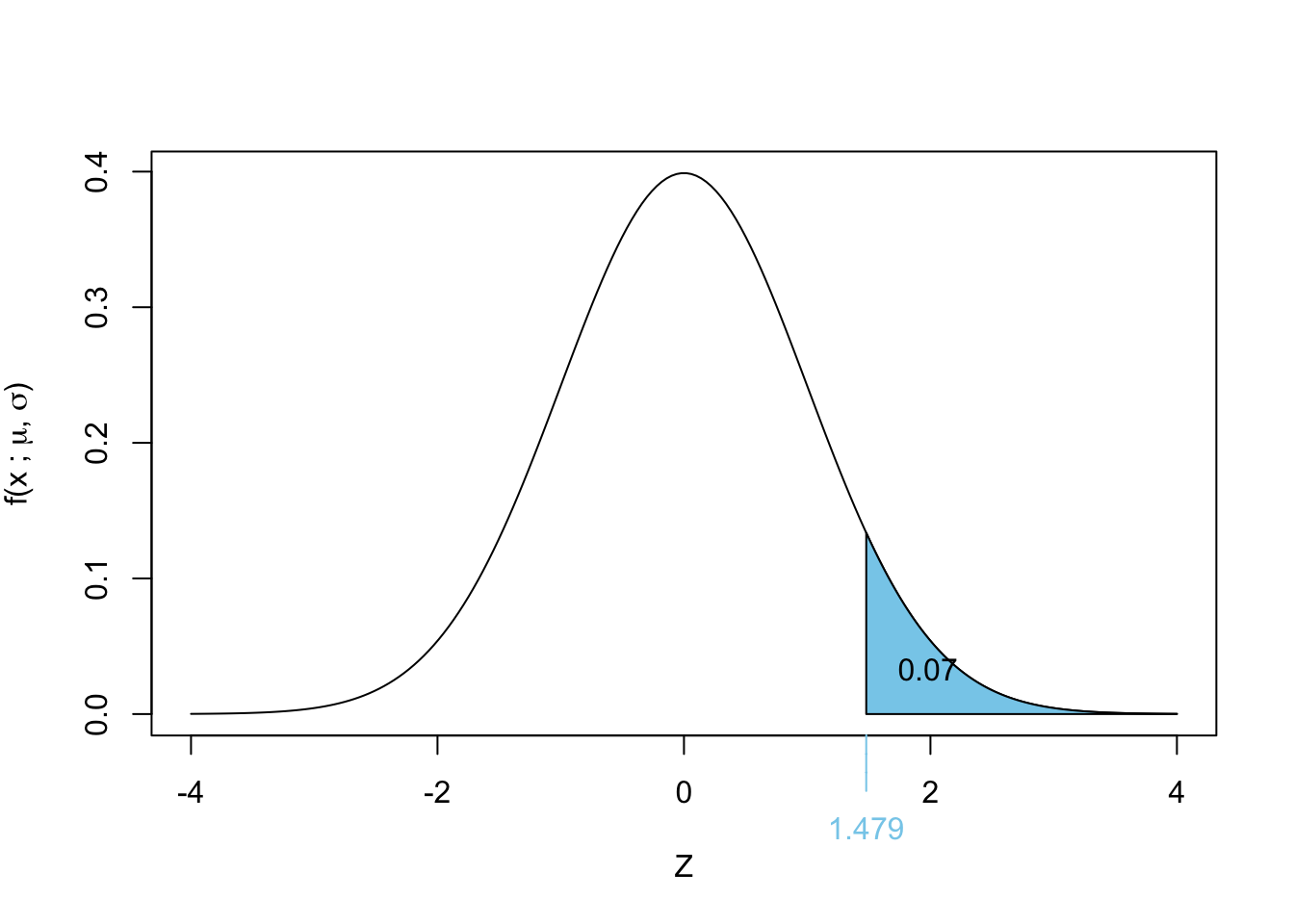
Exercise 2.8 Let \(X_1, X_2, \dots, X_5\) be a random sample from a normal distribution with mean 55 and variance 223. Let

\[ Y = \sum_{i=1}^{5} \frac{(X_i - \bar{X})^2}{223} \]

1. What is the distribution of the random variable \(Y\)?

Solution

Using the result that if \(X_i \sim N(\mu, \sigma^2)\), then:

\[Y = \sum_{i = 1}^n\frac{(X_i - \bar{X})^2}{\sigma^2} \sim \chi^2_{n-1}\]

In this case:

\[ Y = \sum_{i=1}^{5} \frac{(X_i - \bar{X})^2}{223} \sim \chi^2_{4} \]

2. What is the probability that \(\Pr(Y \leq 2)\)?

Solution

\[\begin{align*} \Pr(Y \leq 2) &= \Pr(\chi^2_4 \leq 2) \\ &= 1 - \Pr(\chi^2_4 \geq 2) \\ &= 1 - 0.2642411 \\ &= 0.2642411 \end{align*}\]

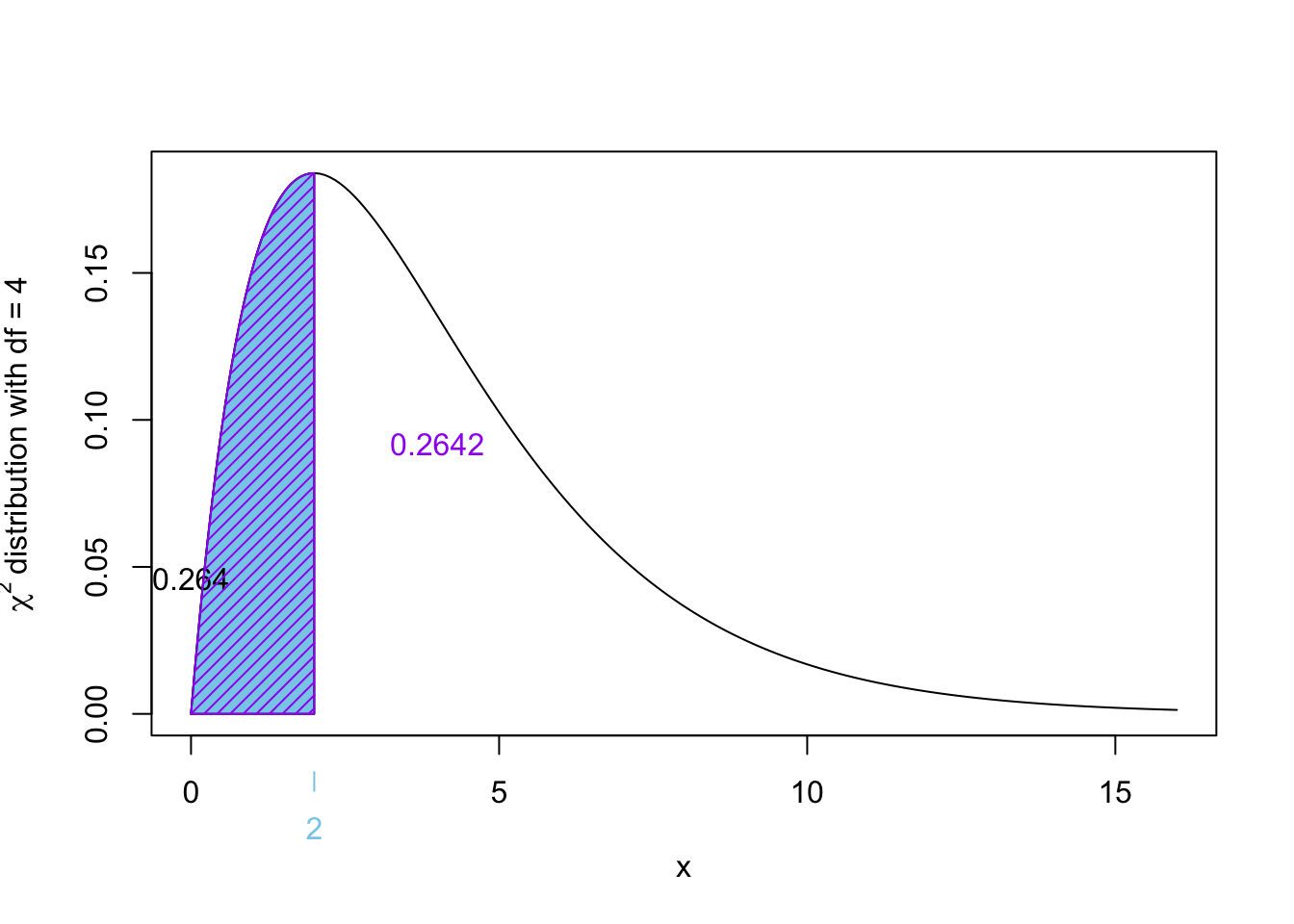
3. How would you calculate this probability in R?

   1. pchisq(2, df = n-1, lower.tail = FALSE)
   2. qchisq(2, df = n-1, lower.tail = FALSE)
   3. pchisq(2, df = n-1)
   4. pchisq(1-2, df = n-1)

Solution

3. is the correct answer:

pchisq(a, df = n-1)                      # option C

[1] 0.2642411

Incorrect answers (wrong tail/ wrong function/ wrong quantile)

pchisq(a, df = n-1, lower.tail = FALSE)  # option A
qchisq(a, df = n-1, lower.tail = FALSE)  # option B

Warning in qchisq(a, df = n - 1, lower.tail = FALSE): NaNs produced

pchisq(1-a, df = n-1)                    # option D

[1] 0.7357589
[1] NaN
[1] 0

4. What is the probability that \(\Pr(2 \leq Y \leq 4)\)?

Solution

\[\begin{align*} \Pr(2 \leq Y \leq 4) &= \Pr(Y \leq 4) - \Pr(Y \leq 2) \\ &= \Pr(\chi^2_4 \leq 4) - \Pr(\chi^2_4 \leq 2) \\ &= \Pr(\chi^2_4 \geq 2) - \Pr(\chi^2_4 \geq 4) \\ &= 0.7357589 - 0.4060058\\ &= 0.329753 \approx 0.33 \end{align*}\]

3 Statistical Inference

Confidence Intervals

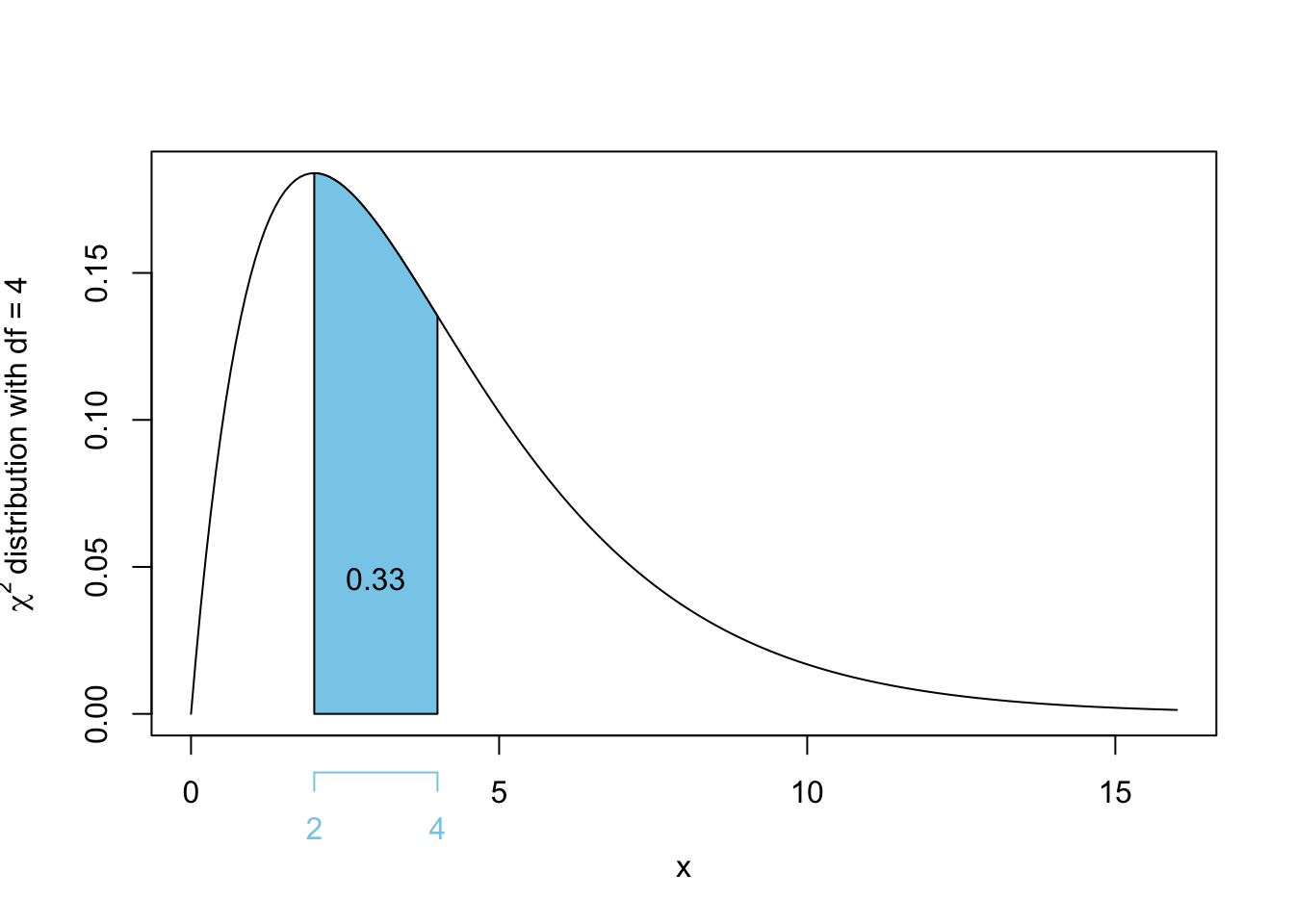
Exercise 3.1 Which of the following best describes the purpose of a confidence interval?

1. It provides a single best estimate of a parameter.
   
2. It describes the variability of a sample statistic.
   
3. It gives a range of plausible values for a population parameter.
   
4. It proves a hypothesis to be true or false.
   

Solution

3. It gives a range of plausible values for a population parameter.

Sample Mean Known \(\sigma\)

Sample Mean unknown \(\sigma\)

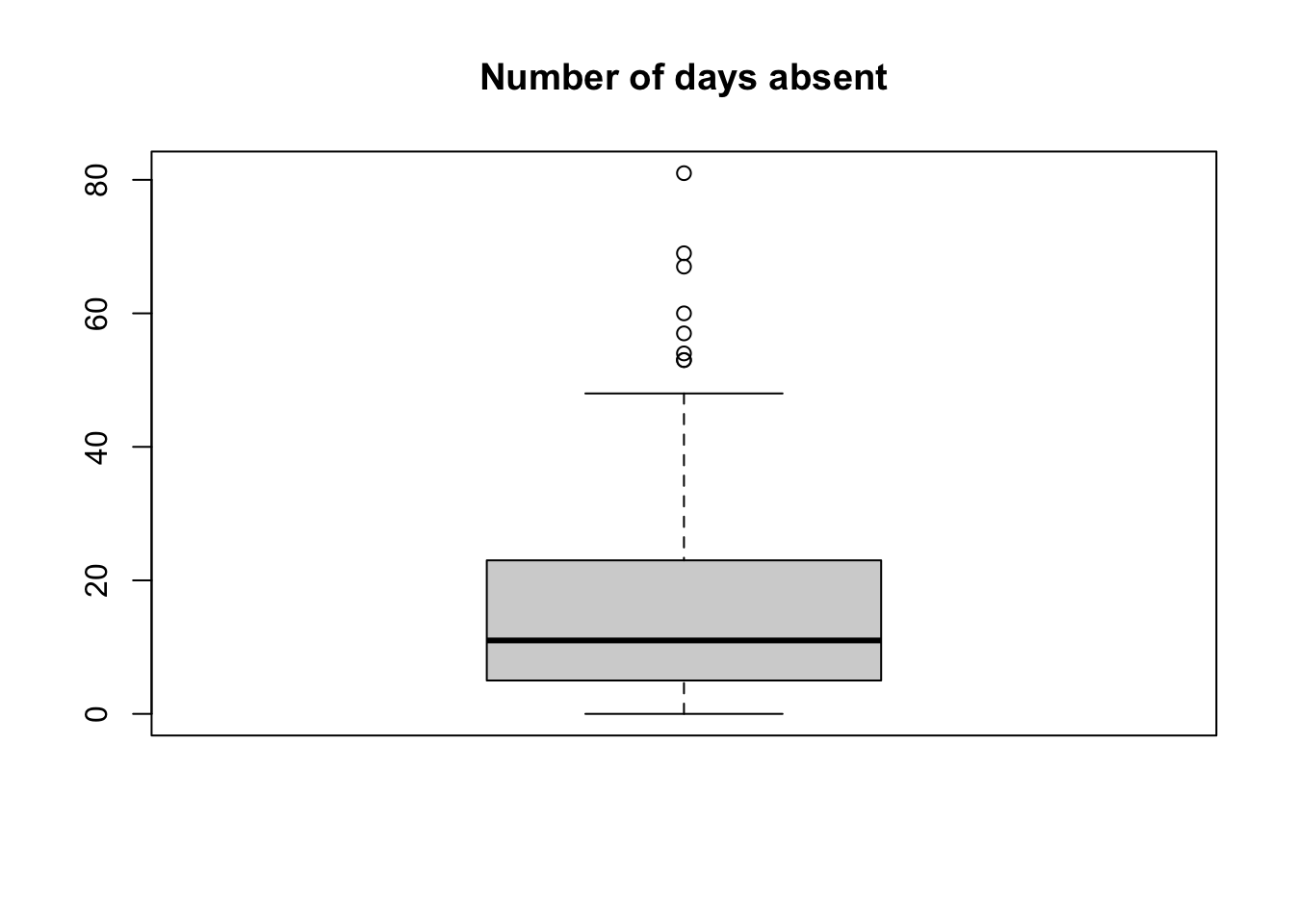
Exercise 3.2 As part of an investigation from Union Carbide Corporation, the following data represent naturally occurring amounts of sulfate S04 (in parts per million) in well water. The data is from a random sample of 24 water wells in Northwest Texas.

1. Do the plots in Figure 3.1 indicate a departure from the assumption of normality in the data?

Figure 3.1

Solution

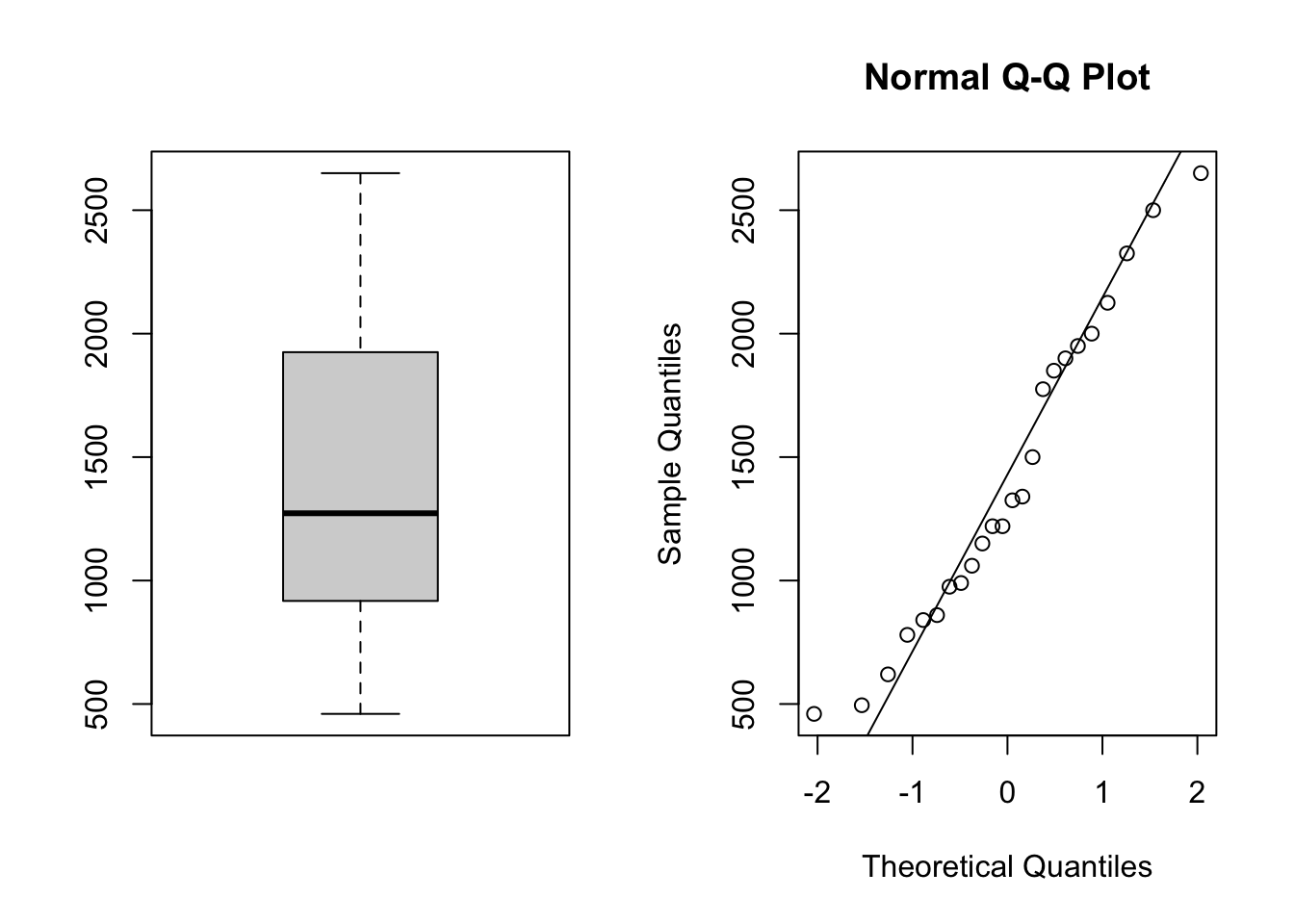
No, there is no indication of a violation of the normality assumption. The boxplot appears roughly symmetric, and there is no systematic curvature or evident outliers in the normal QQ plot.

2. Based on the following summary statistics, estimate the standard error for \(\bar{X}\) (assume that the 24 observations are stored in a vector called data)

   c(mean(data), median(data), sd(data), var(data))

   [1]   1412.9167   1272.5000    636.4592 405080.2536

Solution

\[ \sigma_{\bar X} = \text{StError}(\bar X) = \frac{\sigma}{\sqrt{n}} \]

Since we don’t have \(\sigma\) we will estimate this using:

\[ \hat \sigma_{\bar X} = \frac{s}{\sqrt{n}} = \frac{636.4592}{\sqrt{24}} = 129.9166902 \approx 129.917 \]

3. Construct a 90% confidence interval for \(\mu\).

Solution

Using the \(t\)-table with \(n - 1 = 23\) degrees of freedom we want:

\[\begin{align*} \Pr(t_{23} > t^*) &= 0.05\\ \implies t^* &= 1.714 \end{align*}\]

The 90% confidence interval for \(\mu\) is computed using

\[\begin{align*} \bar x &\pm t^* \sigma_{\bar X}\\ 1412.9167 &\pm 1.714 \times 129.917\\ 1412.9167 &\pm 222.677738\\ (1190.239 &,1635.594 ) \end{align*}\] In words, we are 90% confident that the average sulfate S04 in well water is between 1190.2 and 1635.6 in parts per million.

Sample Proportion

Exercise 3.3 In New York City on October 23rd, 2014, a doctor who had recently been treating Ebola patients in Guinea went to the hospital with a slight fever and was subsequently diagnosed with Ebola. Soon thereafter, an NBC 4 New York/The Wall Street Journal/Marist Poll found that 82% of New Yorkers favored a “mandatory 21-day quarantine for anyone who has come into contact with an Ebola patient.” This poll included responses from 1042 New York adults between October 26th and 28th, 2014.

1. What is the point estimate in this case, and is it reasonable to use a normal distribution to model that point estimate?

Solution

The point estimate, based on a sample size of \(n = 1042\), is \(\hat{p} = 0.82\).

To check whether \(\hat{p}\) can be reasonably modeled using a normal distribution, we check:

• Independence (poll is based on a simple random sample)
  
• Success-failure condition:
  • \(n \hat{p} = 1042 \times 0.82 = 854.44 \geq 10\) (condition met)
  • \(n (1 - \hat{p}) = 1042 \times 0.18 = 187.56 \geq 10\) (condition met)

Since both conditions are met, we can assume the sampling distribution of \(\hat{p}\) follows an approxiamte normal distribution.

2. Estimate the standard error of \(\hat{p}\).

Solution

The standard error is given by:

\[ SE_{\hat{p}} = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \]

Substituting values:

\[ SE_{\hat{p}} = \sqrt{\frac{0.82(1 - 0.82)}{1042}} = \sqrt{\frac{0.82 \times 0.18}{1042}} \approx 0.012 \]

3. Construct a 95% confidence interval for \(\hat{p}\).

Solution

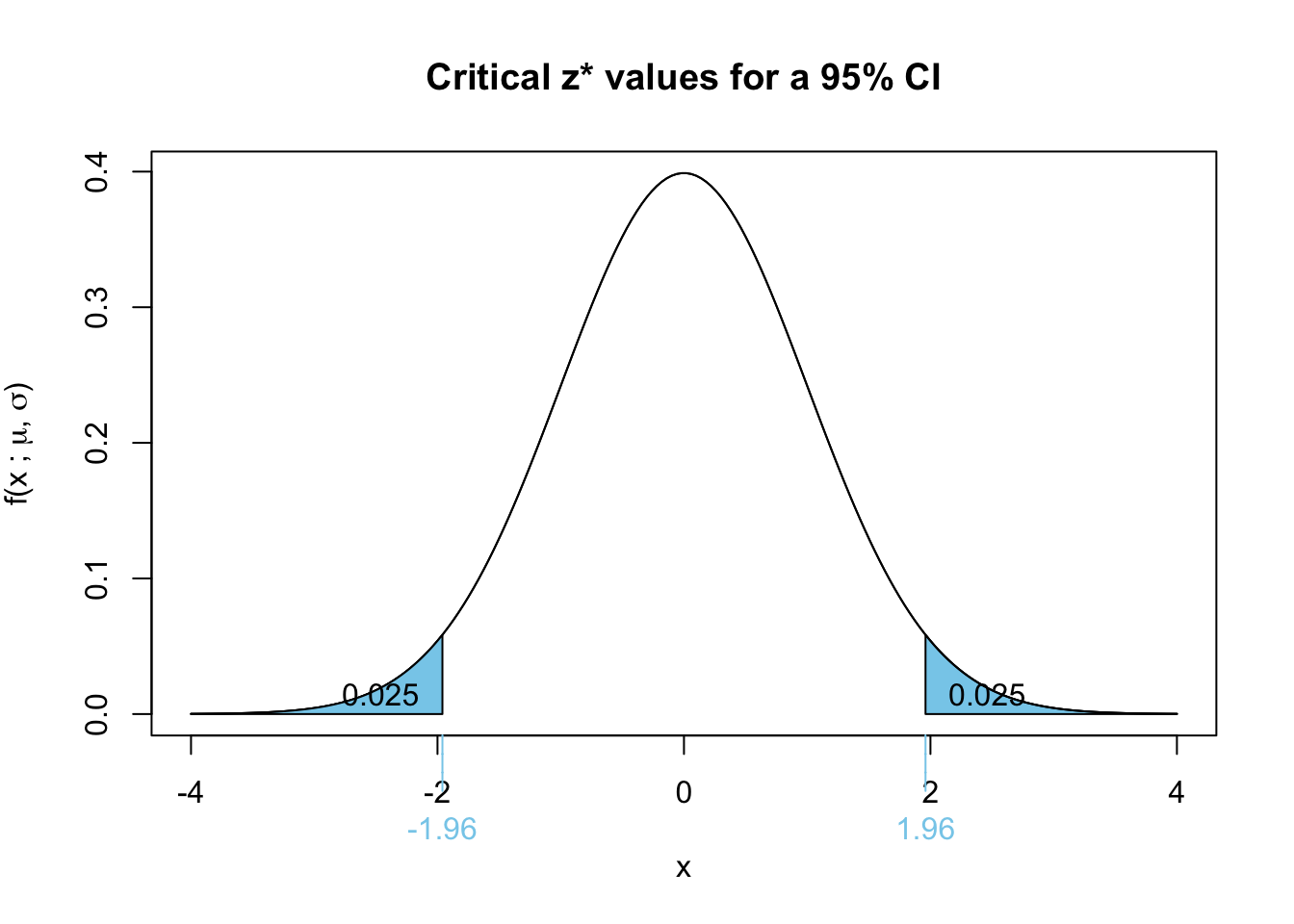
Using \(SE = 0.012\), \(\hat{p} = 0.82\), and the critical value \(z^* = 1.96\) for a 95% confidence level:

\[\begin{align*} \text{Confidence Interval} &= \hat{p} \pm z^* \times SE \\ &= 0.82 \pm 1.96 \times 0.012 \\ &= 0.82 \pm 0.02352 &\text{ans option 1}\\ &= (0.797, 0.843)&\text{ans option 2} \end{align*}\]

Either the point estimate plus/minus the margin of error, or the confidence interval are acceptable final answers.

4. Interpret the confidence interval.

Solution

We are 95% confident that the proportion of New York adults in October 2014 who supported a quarantine for anyone who had come into contact with an Ebola patient was between 0.797 and 0.843.

5. If we instead wanted an 85% confidence interval, the interval would get
   1. wider
   2. narrower
   3. stay the same
   4. There is not enough information to say

Solution

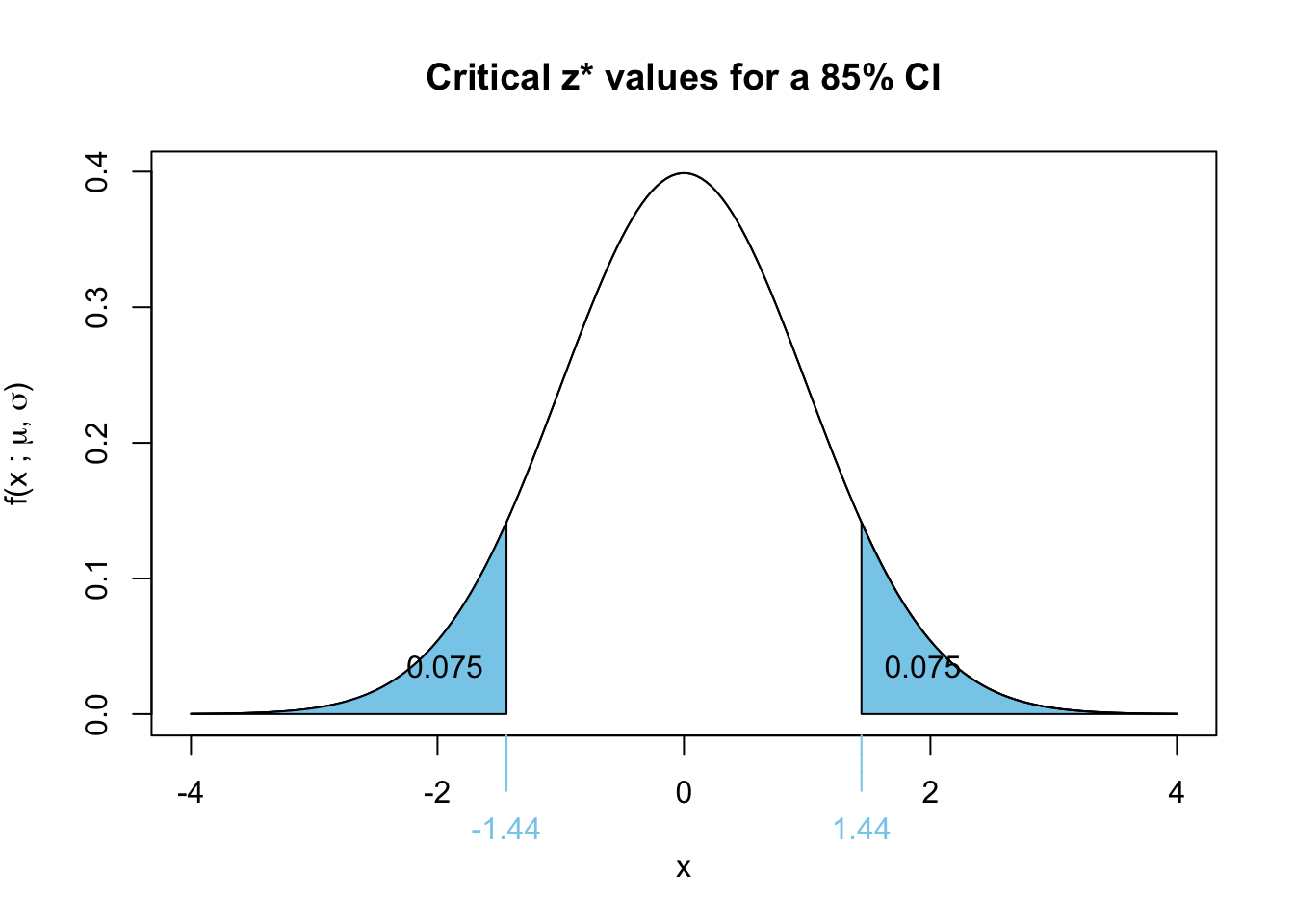
narrower

A lower confidence level corresponds to a smaller \(z^*\) value, which results in a narrower confidence interval.

(a) zstar values

(b) zstar values

Figure 3.2: Left The z* values for a 95% CI. Right The critical z* values of a 85% CI.

Sample Variance