STAT 205: Introduction to Mathematical Statistics
Population
π§π§π»π§π½π§πΎπ§πΏπ§ββοΈπ§π»ββοΈπ§πΌββοΈπ§π½ββοΈπ§πΎββοΈπ§πΏββοΈπ§ββοΈ
π§ββοΈπ§π½ββοΈπ§πΎββοΈπ§πΏββοΈπ§πΎββοΈπ§πΏββοΈπ§π½ββοΈπ§πΏπ§ββοΈπ§π½ββοΈπ§πΏπ§πΌββοΈ
π§πΏββοΈπ§π§π»π§ββοΈπ§π½π§πΎπ§πΎββοΈπ§ββοΈπ§π»ββοΈπ§πΌββοΈπ§π½ββοΈπ§ββοΈ
π§πΏββοΈπ§π§π»π§ββοΈπ§π½π§πΏββοΈπ§πΎπ§πΎββοΈπ§πΎββοΈπ§ββοΈπ§π»ββοΈπ§π½ββοΈ
\[\downarrow \text{SRS}\]
Sample
π§π§πΎπ§πΌββοΈπ§π½ββοΈπ§ββοΈπ§π½ββοΈ
Population Distribution
\[ \begin{align} & f(x;\mu, \sigma) \end{align} \]
Population Parameters
\[ \begin{align} \mu &= ? & \sigma^2 &= ? \end{align} \]
Population
π§π§π»π§π½π§πΎπ§πΏπ§ββοΈπ§π»ββοΈπ§πΌββοΈπ§π½ββοΈπ§πΎββοΈπ§πΏββοΈπ§ββοΈ
π§ββοΈπ§π½ββοΈπ§πΎββοΈπ§πΏββοΈπ§πΎββοΈπ§πΏββοΈπ§π½ββοΈπ§πΏπ§ββοΈπ§π½ββοΈπ§πΏπ§πΌββοΈ
π§πΏββοΈπ§π§π»π§ββοΈπ§π½π§πΎπ§πΎββοΈπ§ββοΈπ§π»ββοΈπ§πΌββοΈπ§π½ββοΈπ§ββοΈ
π§πΏββοΈπ§π§π»π§ββοΈπ§π½π§πΏββοΈπ§πΎπ§πΎββοΈπ§πΎββοΈπ§ββοΈπ§π»ββοΈπ§π½ββοΈ
\[\downarrow \text{SRS}\]
Sample
π§π§πΎπ§πΌββοΈπ§π½ββοΈπ§ββοΈπ§π½ββοΈ
Population Distribution
\[ \begin{align} & f(x; \lambda) = \lambda e^{-\lambda x} & x \geq 0 \end{align} \]
Population Parameters
\[ \begin{align} \lambda &= ? \end{align} \]
Population
π§π§π»π§π½π§πΎπ§πΏπ§ββοΈπ§π»ββοΈπ§πΌββοΈπ§π½ββοΈπ§πΎββοΈπ§πΏββοΈπ§ββοΈ
π§ββοΈπ§π½ββοΈπ§πΎββοΈπ§πΏββοΈπ§πΎββοΈπ§πΏββοΈπ§π½ββοΈπ§πΏπ§ββοΈπ§π½ββοΈπ§πΏπ§πΌββοΈ
π§πΏββοΈπ§π§π»π§ββοΈπ§π½π§πΎπ§πΎββοΈπ§ββοΈπ§π»ββοΈπ§πΌββοΈπ§π½ββοΈπ§ββοΈ
π§πΏββοΈπ§π§π»π§ββοΈπ§π½π§πΏββοΈπ§πΎπ§πΎββοΈπ§πΎββοΈπ§ββοΈπ§π»ββοΈπ§π½ββοΈ
\[\downarrow \text{SRS}\]
Sample
π§π§πΎπ§πΌββοΈπ§π½ββοΈπ§ββοΈπ§π½ββοΈ
Population Distribution
\[ \begin{align} f(x; \alpha, \beta) = \begin{cases} \frac{x^{\alpha - 1}(1 - x)^{\beta - 1}}{\text{B}(\alpha, \beta)} & 0 \leq x \leq 1, \\ 0 & \text{o.w} \end{cases} \end{align} \]
Population Parameters
\[ \begin{align} \alpha = ? && \beta &= ? \end{align} \]
The Normal Distribution, \(f(x;\mu, \sigma)\), has two parameters: \(\mu\) and \(\sigma\). Hence we will need two sets of momentsβ¦
Population Moments
\[ \begin{align} \mu'_1 &= \mathbb{E}[X] = \mu\\ \mu'_2 &=\mathbb{E}[X^2]=\sigma^2 + \mu^2 \end{align} \]
Sample Moments
\[ \begin{align} m'_1 &= \frac{1}{n}\sum_{i=1}^n X_i \\ m'_2 &= \frac{1}{n}\sum_{i=1}^n X_i^2 \end{align} \]
The Exponential Distribution \(f(x;\lambda)\), has only one parameters: \(\lambda\). Hence we need one sets of momentsβ¦
Population Moments
\[ \begin{align} \mu'_1 &= \mathbb{E}[X] = \frac{1}{\lambda} \end{align} \]
Sample Moments
\[ \begin{align} m'_1 &= \frac{1}{n}\sum_{i=1}^n X_i \end{align} \]
Maximum Likelihood Estimation (MLE) is a method for estimating the parameters of a statistical model.
The basic idea behind MLE is to find the values of the parameters that maximize the likelihood function, which measures how well the model explains the observed data.
The plotted likelihood for simulated data from a geometric distribution with \(p\) = 0.3.
For this simulation the MLE is \(\hat p = 0.33\)
The plotted log-likelihood for simulated data from a geometric distribution with \(p\) = 0.3.
Comments
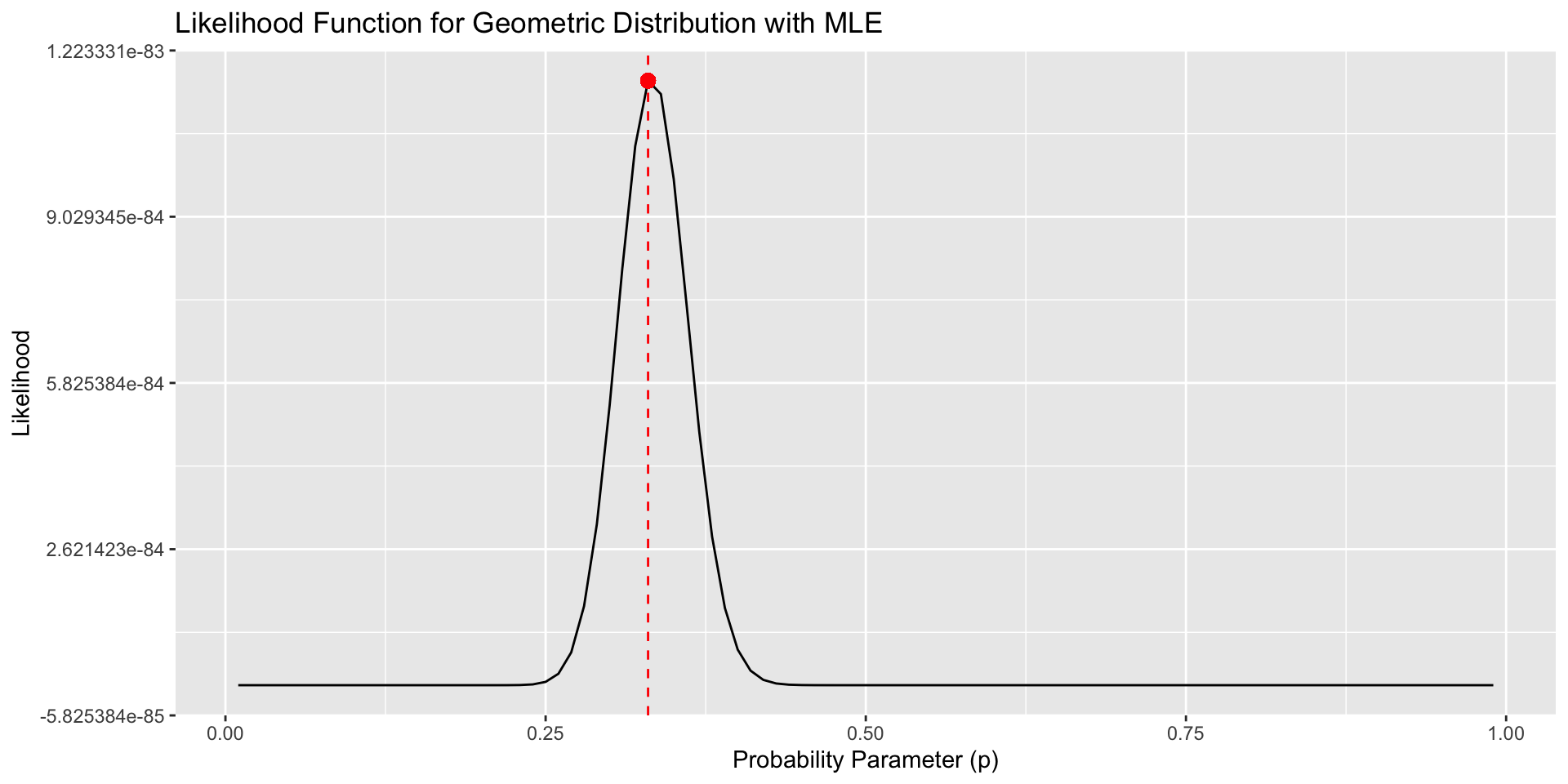
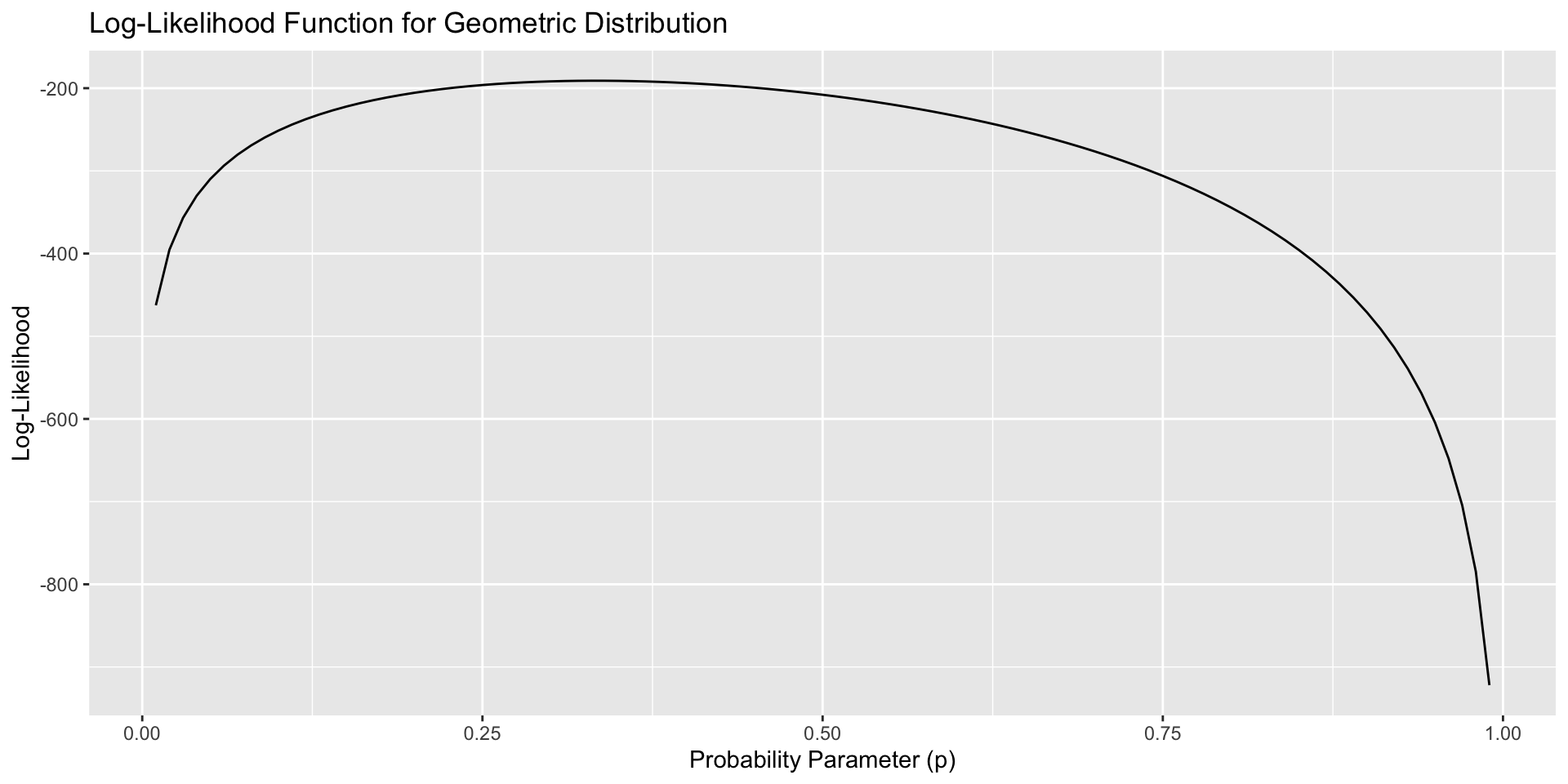
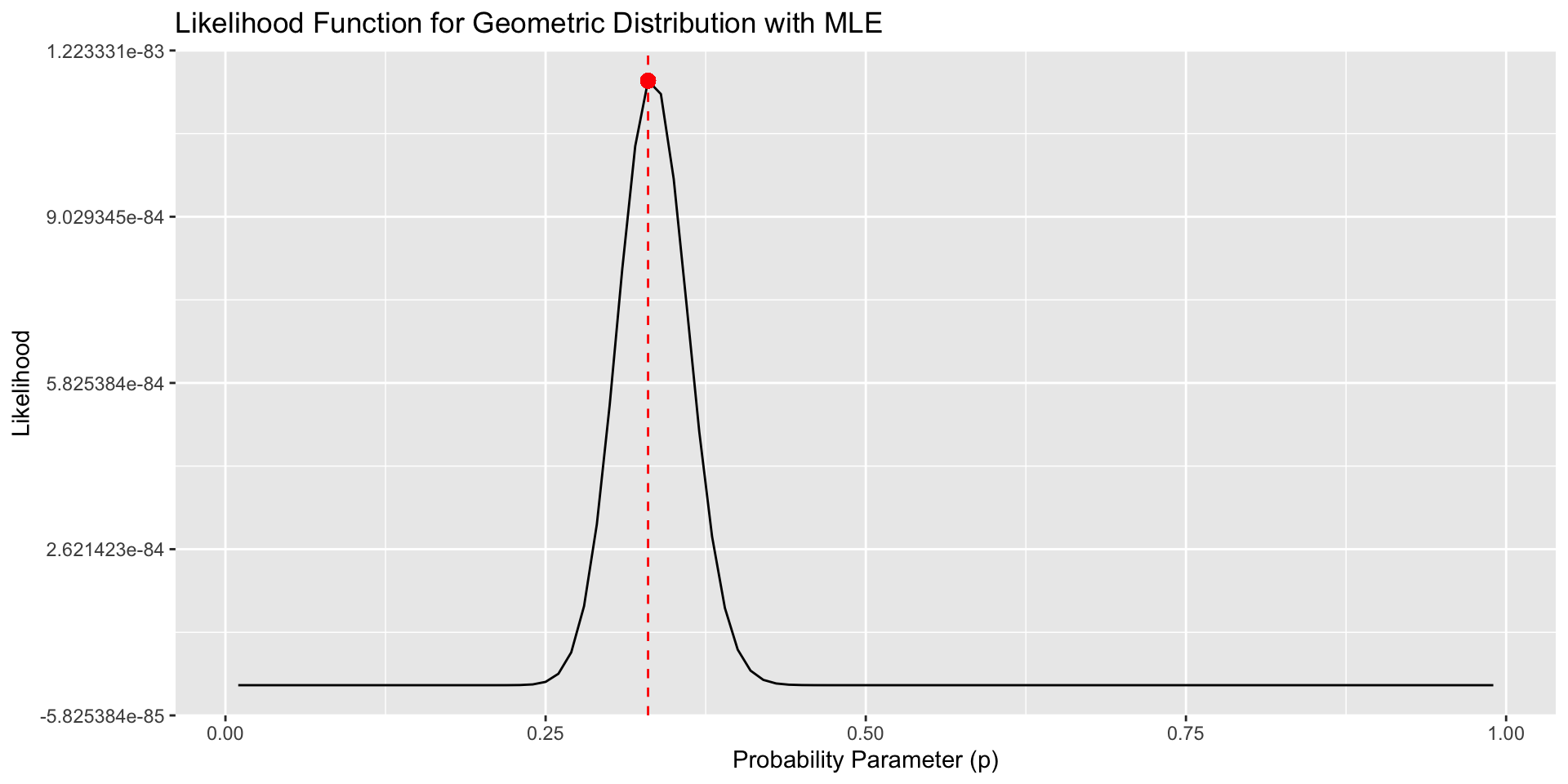
While intuitive and easy to apply, the method of moments usually does not yield βgoodβ estimators (they are not always efficient)
In some cases, the method of moments estimator may coincide with other well-known estimators, providing a unique solution.
However, in more complex models or under certain conditions, the method of moments may not produce a unique estimator.