Lecture 2: Summarizing Data

STAT 205: Introduction to Mathematical Statistics

Dr. Irene Vrbik

University of British Columbia Okanagan

2025-01-18

Outline

This lecture focuses¹ on the mechanics and construction of summary statistics and graphs using R.

Plots

• Scatterplots
• Dot Plot
• Histograms
• Boxplot

Measures of central tendency:

• Mean (Average) and Median

Measures of dispersion:

• Variance (and Standard Deviation) and Interquartile Range (IQR)

1. Some review of R (Rstudio and Quarto Supplementary Material time permitting)

Types of Data (Review)

Here’s a brief overview of how each data type is coded in R:

Numerical (quantitative)

• Continuous (numeric)

  x <- 3.14
  class(x)

  [1] "numeric"

• Discrete (integer)

  y <- 5L # L indicates integer
  class(y)

  [1] "integer"

Categorical (qualitative)

• nominal (factor)

  class(gender <- factor(c("male", "female", "male")))
  gender

  [1] "factor"
  [1] male   female male  
  Levels: female male

• ordinal (ordered factor)

  dose <- factor(c("High", "Medium", "Low", "High"),
          levels = c("Low", "Medium", "High"),
          ordered = TRUE)
  class(dose)
  dose

  [1] "ordered" "factor" 
  [1] High   Medium Low    High  
  Levels: Low < Medium < High

• Specify the

Categorical as numbers

Sometimes categorical variables are represented as numbers:

• 0 = never married, 1 = married, 2 = divorced
• 1 = Strongly disagree, 2 = disagree, 3 = neutral, 4 = somewhat agree, 5 = strongly agree

While it will sometimes be appropriate to treat these variables as numeric, we will often need to coerce¹ them to the proper data type.

1. In R, coercion refers to the process of converting an object from one data type to another (typically achieved using as._<type>_ functions; see examples)

Other R Data Types

• Character Data Type (character or string):

  • Represents text data.

  z <- "hello world!"; class(z) # ';' for statement separator

  [1] "character"

• Logical Data Type (logical or boolean):

  • Represents binary or Boolean values (TRUE or FALSE).

  • Used for logical conditions and comparisons.

  (is_male <- gender == "male")

  [1]  TRUE FALSE  TRUE

  class(is_male)

  [1] "logical"

Coercion

Example 1 character to numeric

x <- "42"          
x

[1] "42"

class(x)

[1] "character"

y <- as.numeric(x)
y

[1] 42

class(y)

[1] "numeric"

If stored in a data frame,

df <- data.frame(x,y, z=c("apple","orange"), w=c(T,F))
str(df)

'data.frame':   2 obs. of  4 variables:
 $ x: chr  "42" "42"
 $ y: num  42 42
 $ z: chr  "apple" "orange"
 $ w: logi  TRUE FALSE

Aside

In my lecture slides, I will be print my data frames in a a paged table¹ display which presents the structure of the created data frame including:

• The dimensions of the data frame (number of rows and columns).
• The names and types of each column.

df

1. this can be obtained by setting df-print: paged in the YAML

Coercion (cont’d)

Example 2 marital status

# class: "numeric"
(mstat <- c(0, 2, 1, 1, 0)) 

[1] 0 2 1 1 0

# class: "factor"
(mstat <- as.factor(mstat)) 

[1] 0 2 1 1 0
Levels: 0 1 2

We can assigns more descriptive labels to each level:

mstat <- factor(
  mstat, 
  levels = 0:2, 
  labels = c("never married", "married", "divorced")
)

Data Structures

In R, there are several data structures for organizing and storing data.

Vectors: a collection of elements of the same data type. Example:

nums <- c(1.5, 2.3, 3.7)
fruit <- c("apple", "orange", "banana")

Matrices: A two-dimensional data structure with elements of the same data type. E.g.

(my_matrix <- matrix(1:6, nrow = 2, ncol = 3))

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

Note: if you have more than one data type in vectors/matrices, it will try and pick one that makes the most sense.

vec <- c(1, "apple", TRUE)
vec

[1] "1"     "apple" "TRUE" 

class(vec)

[1] "character"

Lists: A collection of elements that can be of different data types. Examples

(my_list <- 
   list(nums, my_fruit = fruit, tf = TRUE, 
    integer = 42L, my_matrix = my_matrix))

[[1]]
[1] 1.5 2.3 3.7

$my_fruit
[1] "apple"  "orange" "banana"

$tf
[1] TRUE

$integer
[1] 42

$my_matrix
     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

iClicker: Data types

iClicker

Exercise 1 (Data Types in R) What is the correct R data type for representing ordered categories like "Low", "Medium", and "High"?

1. Numeric
2. Factor
3. Ordered Factor
4. Character

Datasets

Now that we have had a refresher in R, let’s load the openinto package as well as the loan dataset

library(openintro) # load the library
data(loan50)       # loads the loan50 dataset from the openintro library.
loan50             # prints the contents of the data; see ?loan50

loan50 will look different for you.

Data Frame

• The most common data structure we will be working with is a data.frame.

• In R, a data frame is a two-dimensional, tabular data structure similar to a spreadsheet or a SQL table.

• Rows represent individual observations or cases, and columns represent variables or attributes associated with those observations.

• Columns can have different data types.

this will look different than a normal data frame when called in R

Some packages will store data into tibbles which are enhanced versions of data frames.

Iris Data frame

class(iris)
iris

[1] "data.frame"

Indexing Vectors

In R there are several ways for indexing or subsetting elements in a data structure. Recall objects we created earlier:

fruit

[1] "apple"  "orange" "banana"

For vectors, [i] is used to extract the element at index i.

fruit[3] # extracts the third element of the vector

[1] "banana"

fruit[c(1,3)] # extracts the first and third element

[1] "apple"  "banana"

Indexing Matrices

Recall the matrix we defined earlier:

my_matrix

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

For matrices, [i, j] is used to extract the element in the \(i\)th row and \(j\)th column.

my_matrix[1,3] 
my_matrix[2,] # 2nd row
my_matrix[,3] # 3rd column

[1] 5
[1] 2 4 6
[1] 5 6

In R there are several ways for indexing or subsetting elements in a data structure.

Indexing Lists

For lists, [[i]] is used to extract the \(i\)th element.

my_list

[[1]]
[1] 1.5 2.3 3.7

$my_fruit
[1] "apple"  "orange" "banana"

$tf
[1] TRUE

$integer
[1] 42

$my_matrix
     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

my_list[[1]]

[1] 1.5 2.3 3.7

my_list[[2]]

[1] "apple"  "orange" "banana"

my_list[[3]]

[1] TRUE

my_list[[4]]

[1] 42

Alternative you can use the $ operator for indexing named elements in list

my_list$my_fruit

[1] "apple"  "orange" "banana"

Indexing Data Frames

We can use [i, j] to extract the \(i\)th row and \(j\)th column from data frames

iris[,1]

  [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9

Similarly the $ operator can be used to extract columns from data frames

iris$Sepal.Length

  [1] 5.1 4.9 4.7 4.6 5.0 5.4 4.6 5.0 4.4 4.9 5.4 4.8 4.8 4.3 5.8 5.7 5.4 5.1
 [19] 5.7 5.1 5.4 5.1 4.6 5.1 4.8 5.0 5.0 5.2 5.2 4.7 4.8 5.4 5.2 5.5 4.9 5.0
 [37] 5.5 4.9 4.4 5.1 5.0 4.5 4.4 5.0 5.1 4.8 5.1 4.6 5.3 5.0 7.0 6.4 6.9 5.5
 [55] 6.5 5.7 6.3 4.9 6.6 5.2 5.0 5.9 6.0 6.1 5.6 6.7 5.6 5.8 6.2 5.6 5.9 6.1
 [73] 6.3 6.1 6.4 6.6 6.8 6.7 6.0 5.7 5.5 5.5 5.8 6.0 5.4 6.0 6.7 6.3 5.6 5.5
 [91] 5.5 6.1 5.8 5.0 5.6 5.7 5.7 6.2 5.1 5.7 6.3 5.8 7.1 6.3 6.5 7.6 4.9 7.3
[109] 6.7 7.2 6.5 6.4 6.8 5.7 5.8 6.4 6.5 7.7 7.7 6.0 6.9 5.6 7.7 6.3 6.7 7.2
[127] 6.2 6.1 6.4 7.2 7.4 7.9 6.4 6.3 6.1 7.7 6.3 6.4 6.0 6.9 6.7 6.9 5.8 6.8
[145] 6.7 6.7 6.3 6.5 6.2 5.9

Data description

While you can see a full description on the website, you could also type the following into the Console you can obtain the help documentation associated with that object or function.

?loan50

Other useful function for inspecting your data include:

str(loan50)   # prints data type and the first few values of each variable.
head(loan50)  # display the first few rows of a data frame
View(loan50)  # used in RStudio to open a data viewer (i.e. spreadsheet) 

Data Structure

• A benefit of looking at the structure of a data frame using str() has the benefit of learning the data type of each variable.

• It is always important the data is coded as we expect (especially true when reading data into R using read.csv).

• The data type will dictate which summary statistics and visualizations are most appropriate.

• Recall: categorical variables are represented using numbers.

• For numerical data, we can use summary statistics like mean, and plots like scatterplots, but these don’t make a ton of sense for categorical data.

we’ll be working with data frames most of the time

• A data frame is a two-dimensional tabular data structure in R, similar to a spreadsheet (e.g., Excel).

• It is used to store datasets where:

  • Rows represent individual observations or cases.

  • Columns represent variables (attributes).

Structure of loan50

str(loan50)

tibble [50 × 18] (S3: tbl_df/tbl/data.frame)
 $ state                  : Factor w/ 51 levels "","AK","AL","AR",..: 32 6 41 6 36 16 35 25 11 11 ...
 $ emp_length             : num [1:50] 3 10 NA 0 4 6 2 10 6 3 ...
 $ term                   : num [1:50] 60 36 36 36 60 36 36 36 60 60 ...
 $ homeownership          : Factor w/ 3 levels "rent","mortgage",..: 1 1 2 1 2 2 1 2 1 2 ...
 $ annual_income          : num [1:50] 59000 60000 75000 75000 254000 67000 28800 80000 34000 80000 ...
 $ verified_income        : Factor w/ 4 levels "","Not Verified",..: 2 2 4 2 2 3 3 2 2 3 ...
 $ debt_to_income         : num [1:50] 0.558 1.306 1.056 0.574 0.238 ...
 $ total_credit_limit     : int [1:50] 95131 51929 301373 59890 422619 349825 15980 258439 87705 330394 ...
 $ total_credit_utilized  : int [1:50] 32894 78341 79221 43076 60490 72162 2872 28073 23715 32036 ...
 $ num_cc_carrying_balance: int [1:50] 8 2 14 10 2 4 1 3 10 4 ...
 $ loan_purpose           : Factor w/ 14 levels "","car","credit_card",..: 4 3 4 3 5 5 4 3 3 4 ...
 $ loan_amount            : int [1:50] 22000 6000 25000 6000 25000 6400 3000 14500 10000 18500 ...
 $ grade                  : Factor w/ 8 levels "","A","B","C",..: 3 3 6 3 3 3 5 2 2 4 ...
 $ interest_rate          : num [1:50] 10.9 9.92 26.3 9.92 9.43 ...
 $ public_record_bankrupt : int [1:50] 0 1 0 0 0 0 0 0 0 1 ...
 $ loan_status            : Factor w/ 7 levels "","Charged Off",..: 3 3 3 3 3 3 3 3 3 3 ...
 $ has_second_income      : logi [1:50] FALSE FALSE FALSE FALSE FALSE FALSE ...
 $ total_income           : num [1:50] 59000 60000 75000 75000 254000 67000 28800 80000 34000 192000 ...

Plotting data

Scatterplots

Scatterplots are useful for visualizing the relationship between two numerical variables. Create scatterplots in R using:

plot(x = loan50$annual_income, y = loan50$loan_amount)

or alternatively:

attach(loan50)
plot(annual_income, loan_amount, xlab = "Annual Income (in dollars $)",
     ylab = "Loan Amount (in dollars $)", 
     main = "Scatterplot of Annual Income vs Loan Amount")

Important

When you attach() a dataframe, the column names of that data frame become directly accessible without specifying the data frame name.

Scatterplots

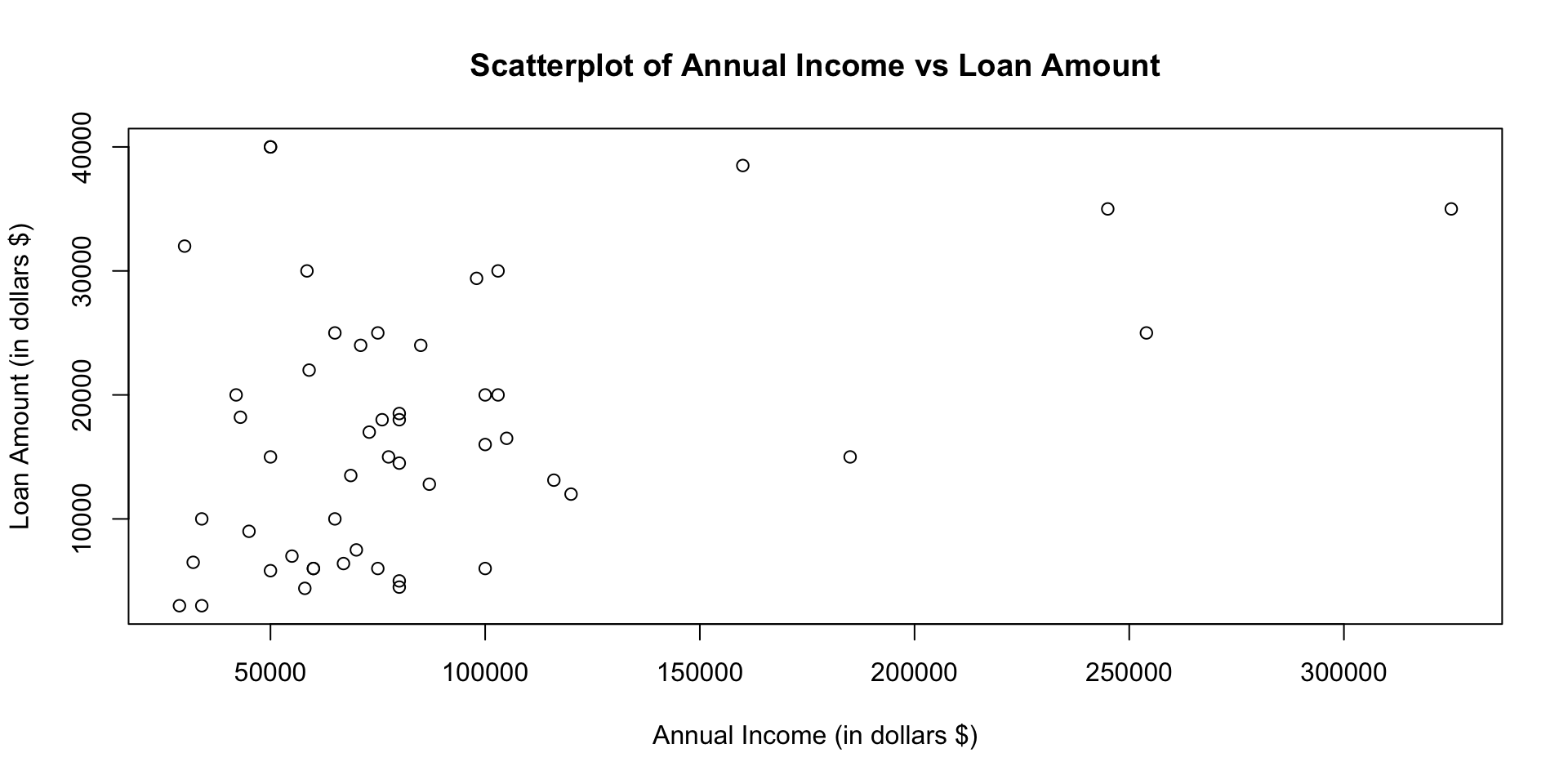
Scatterplot in ggplot

Alternatively we can create a scatterplot using the popular ggplot package

# Load the ggplot2 library
library(ggplot2)

ggplot(loan50, aes(x = annual_income, y = loan_amount)) +
  geom_point() +
  scale_x_continuous(
    labels = scales::dollar_format()
  ) +
  scale_y_continuous(
    labels = scales::dollar_format()
  ) +
  labs(
    title = "Scatterplot of Annual Income vs Loan Amount",
    x = "Annual Income",
    y = "Loan Amount"
  )

Scatterplot in ggplot

Dot Plot

A dot plot is a one-variable scatterplot

stripchart(interest_rate, method = "stack", pch = 19, offset = .5, at = 0, 
           col = "steelblue", xlab = "Interest Rates (in %)", cex = 2)

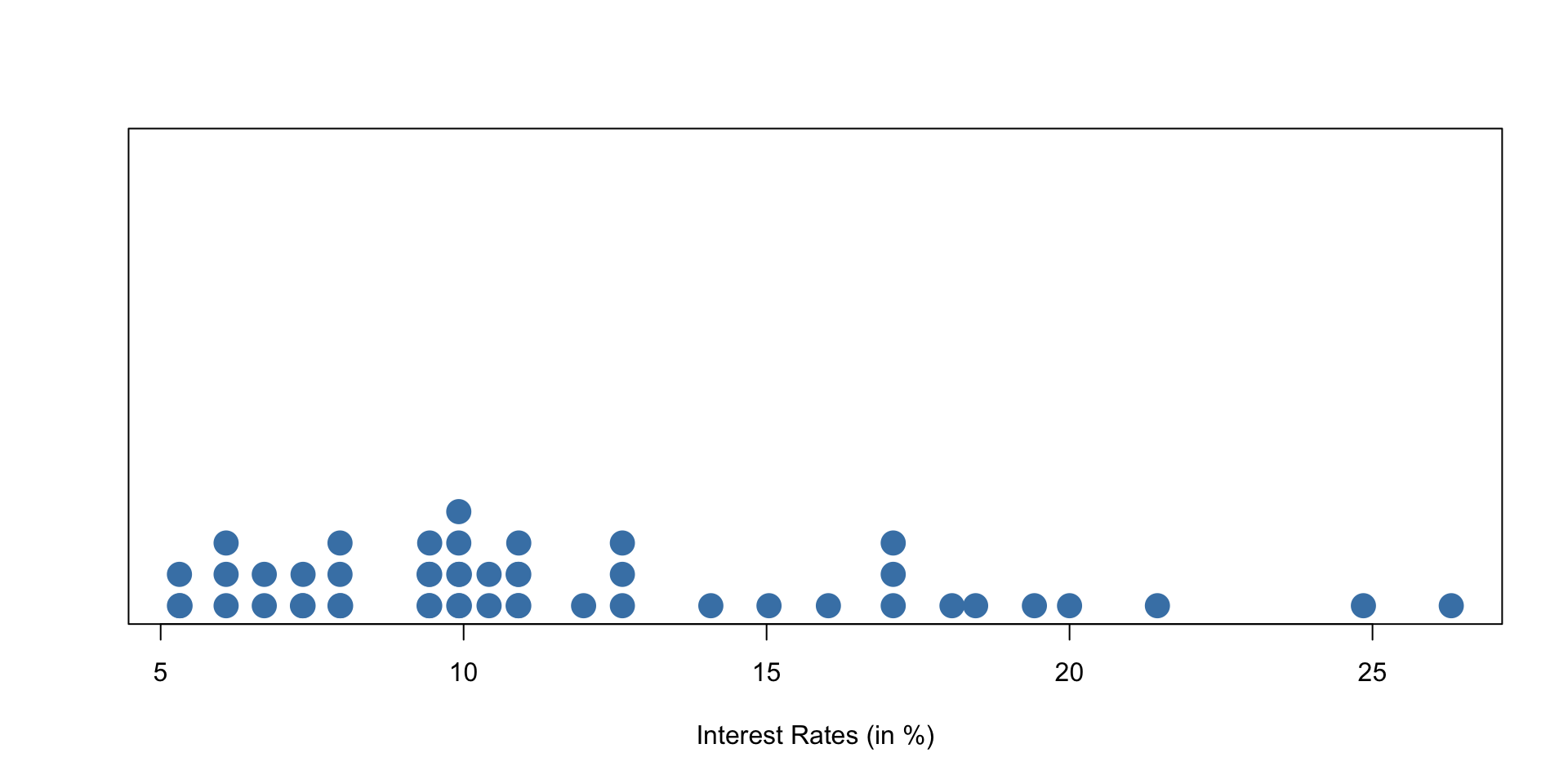
An example of a dotchart using the interest rate of 50 loans

Notice that some numbers appear more than once; there are non integer values

interest_rate[1:5]

[1] 10.90  9.92 26.30  9.92  9.43

Stacked dot plot

# Create a stacked dot plot using ggplot2
ggplot(loan50, aes(x = interest_rate)) +
    geom_dotplot() + labs(x = "Interest Rate (in %)") 

Mean (Average)

• The mean, often called the average, is a common way to measure the center of a distribution of data.

• To compute the mean interest rate, we add up all the interest rates and divide by the number of observations.

• In R this is accomplished using the mean() function.

  (mean_value = mean(interest_rate))

  [1] 11.5672

Mean (average) formula

Mean (Average) formula for sample vs. population

The sample mean is often labeled \(\overline{x}\). The sample mean can be computed as the sum of the observed values divided by the number of observations:

\[ \overline{x} = \frac{x_1 + x_2 + \dots + x_n}{n} \]

where \(x_1, \dots x_n\) represent the \(n\) observed values. The population mean is given by

\[ \mu = \frac{x_1 + x_2 + \dots + x_N}{N} \]

Sample vs. Population Mean

• The population mean is also computed the same way but is denoted as \(\mu\). It is often not possible to calculate \(\mu\) since population data are rarely available.

• The sample mean is a sample statistic, and serves as a point estimate of the population mean.

• This estimate may not be perfect, but if the sample is good (representative of the population), it is usually a pretty good estimate.

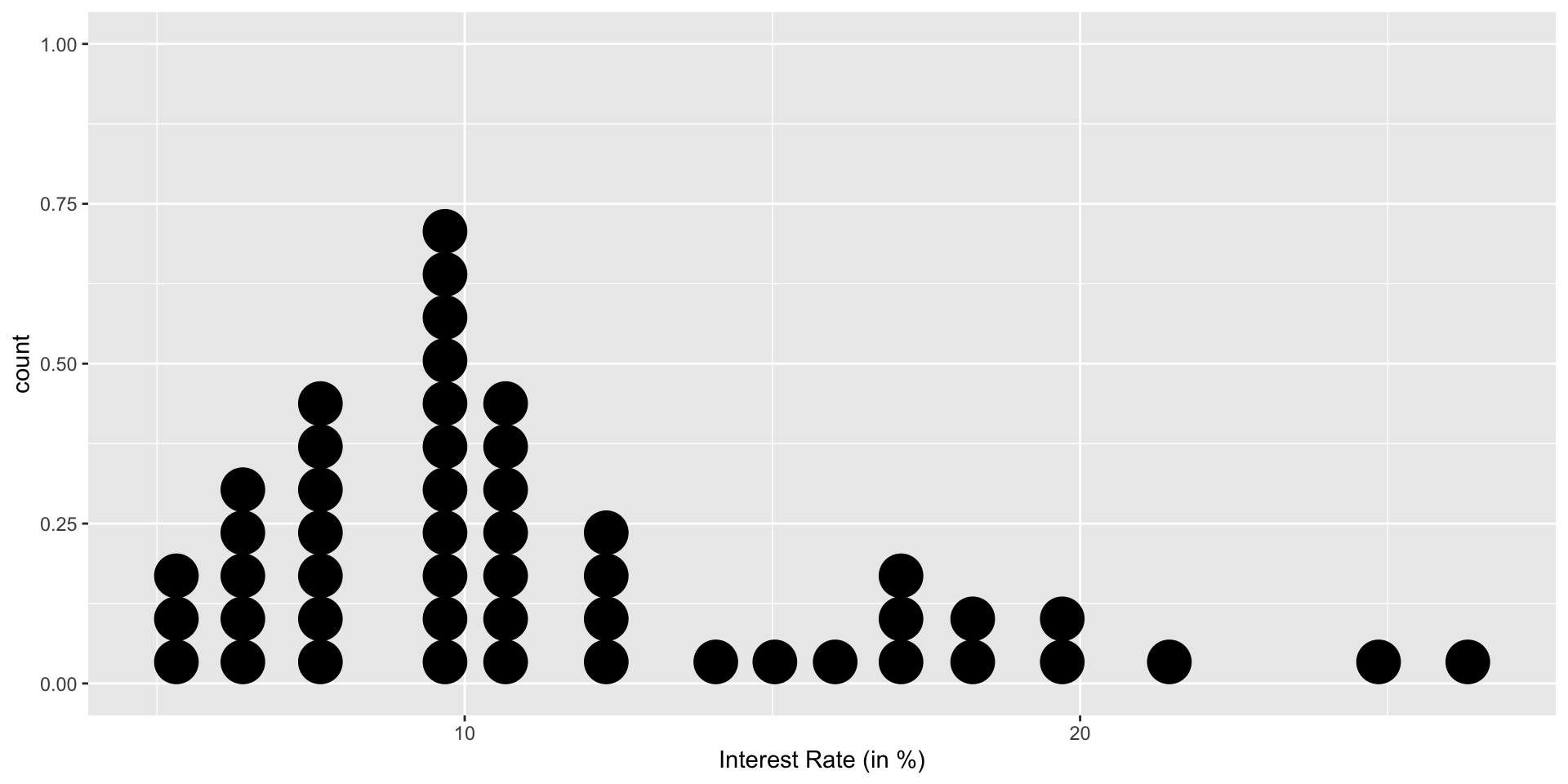
Dotplot with mean

# Create a dot plot with mean using ggplot2
ggplot(loan50, aes(x = interest_rate)) +
  geom_dotplot() + labs(x = "Interest Rate (in %)") +
  geom_point(aes(x = mean_value, y = 0), color = "red", size = 5, shape = 17) 

A stacked dot plot of interest_rate for the loan50 data set. The distribution’s mean is shown as a red triangle.

You can think of the mean as the balancing point of a distribution.

Median

• The median is a measure of central tendency that represents the middle value in a dataset when it is ordered from least to greatest.

• It is a robust¹ statistic, meaning that it is not sensitive to extreme values or outliers in the data.

• The median is also referred to as the 50th percentile because it divides the dataset into two equal halves. Fifty percent of the observations are below the median, and fifty percent are above it.

1. This is in contrast to the mean, which can be heavily influenced by extreme values.

Dot plot with median

# Create a dot plot with mean and median using ggplot2

median_value = median(interest_rate)
ggplot(loan50, aes(x = interest_rate)) +
  geom_dotplot() + labs(x = "Interest Rate (in %)") +
  geom_point(aes(x = mean_value, y = 0), color = "red", size = 5, shape = 17) +
  geom_point(aes(x = median_value, y = 0), color = "green", size = 5, shape = 15)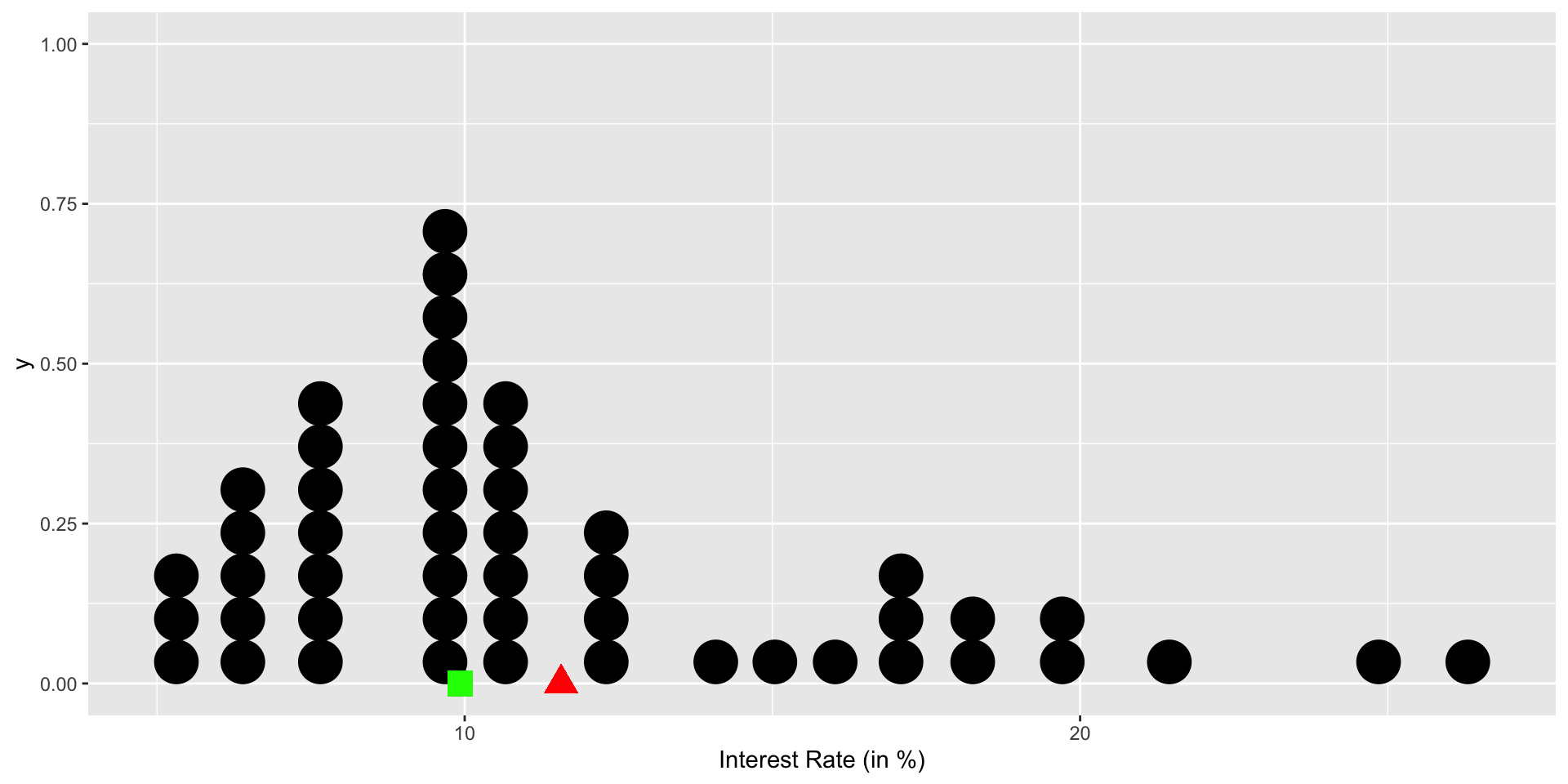 

A stacked dot plot of interest_rate for the loan50 data set. The distribution’s mean is shown as a red triangle, the median is shown as a green square.

Mode

The mode is the value or category in a dataset that occurs most frequently.

• For Numerical Data¹: The mode is the value that appears most often.

  • e.g. {2, 3, 3, 4, 4, 4, 5}, the mode is 4

• For Categorical Data: The mode represents the category with the highest frequency.

  • e.g {red, blue, blue, green, red, blue}, the mode is blue.

1. The mode is more practical for categorical data

Histograms

• Dot plots show the exact value for each observation. This is useful for small data sets, but they can become hard to read with larger samples.

• Rather than showing the value of each observation, we prefer to think of the value as belonging to a bins¹

5 to 10	10 to 15	15 to 20	20 to 25	25 to 30
26	12	9	2	1

1. The range is divided into equal-width intervals or bins. Each bin represents a specific range of values.

Histogram in R

hist(interest_rate) 

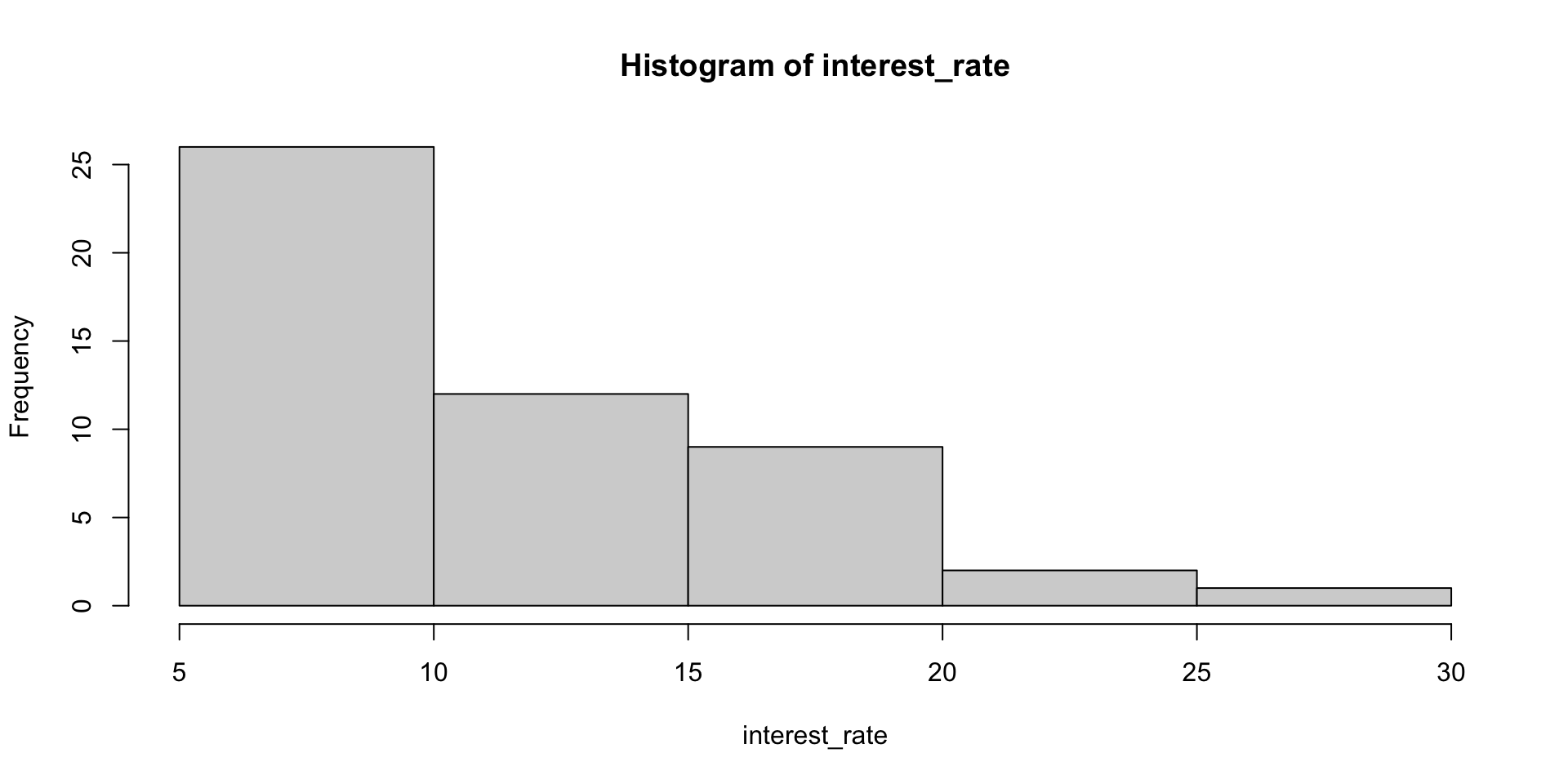
Bins

• Histograms provide a view of the data density. Higher bars represent where the data are relatively more common.

• Usually R will do a pretty good job of picking the bin size but we can play around with it.

• The breaks argument represents the suggested number¹ of bins you want the data to be divided into. R will then automatically determine the appropriate bin width.

1. The function will try to create approximately the specified number of breaks but may adjust the bin widths for better alignment with data points.

More breaks

hist(interest_rate, breaks = 12, main = "", 
     xlab = "Interest Rate (in %)") # output on next slide

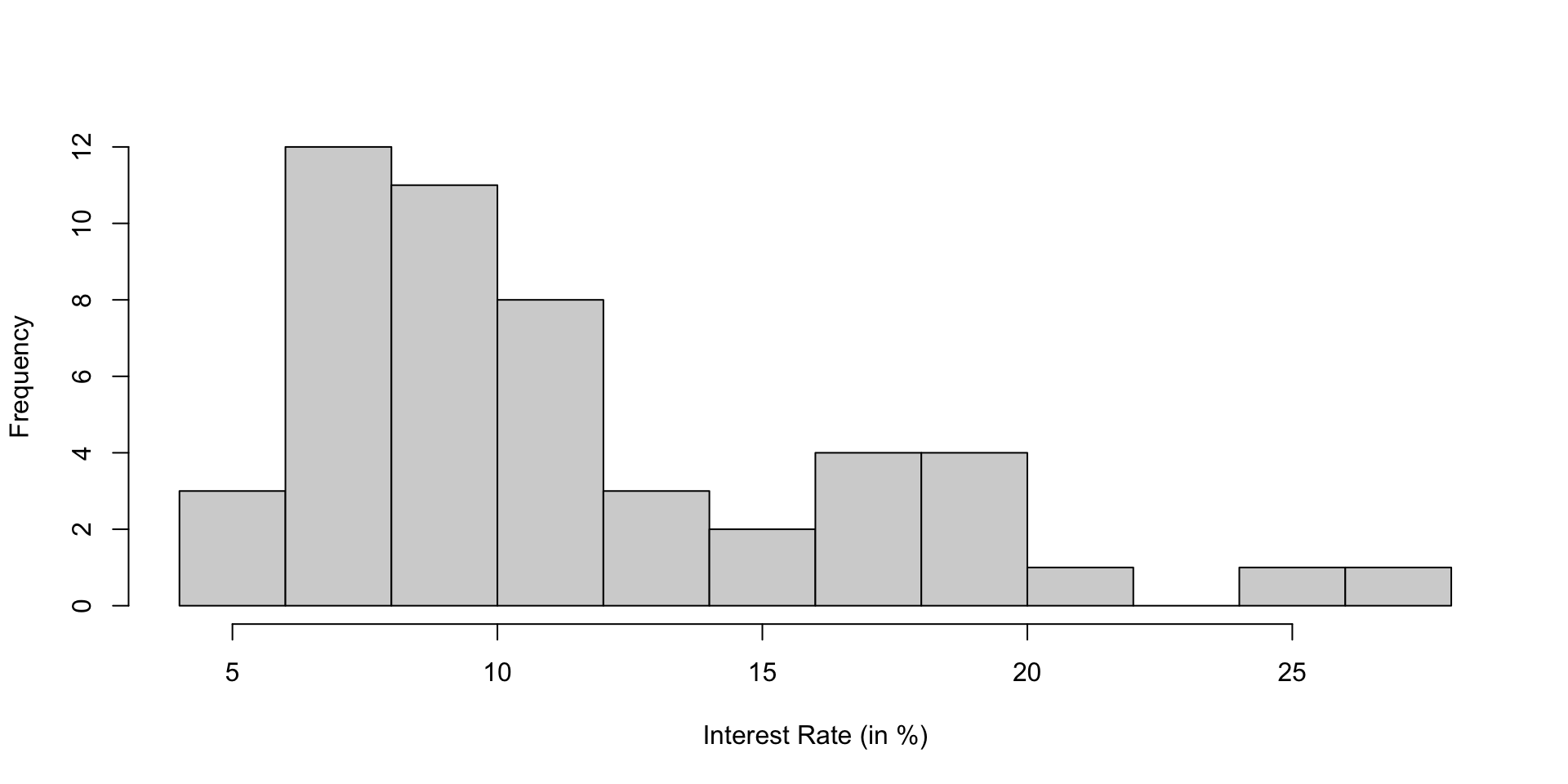
4 to 6	6 to 8	8 to 10	10 to 12	12 to 14	14 to 16	16 to 18	18 to 20	20 to 22	22 to 24	24 to 26	26 to 28
3	12	11	8	3	2	4	4	1	0	1	1

A histogram of interest_rate. This distribution is strongly skewed to the right

Shapes of Distributions

Histograms are especially convenient for describing the shape of the data distribution.

• Symmetric: The distribution is balanced on both sides of the center.

• Skewed: The distribution has a longer tail on one side, either to the right (positive skew) or left (negative skew).

• Uniform: The distribution is flat and lacks pronounced peaks or troughs.

Central tendencies for skewed distributions

• The median is particularly useful when describing the center of a distribution in the presence of skewed or asymmetrical datasets (see Shapes of Distributions)

• In a right/positively skewed distribution the median is typically less than the mean (see Dot plot with median), and in a left/negatively skewed distribution, the median is greater than the mean.

Characteristics of Histograms

We can also identify the “center” of the distribution.

• For a symmetric distribution, the center is typically the peak of the density.
• For skewed distributions, the center may be closer to the peak on the longer tail.

By examining the width of the distribution histograms can also assess how “spread” out the values are.

• A wider distribution indicates higher dispersion, while a narrower distribution suggests lower dispersion.

Histogram with mean/median

Consider the final exam score for a STAT course:

set.seed(888)
test_scores <- 100*rbeta(500, shape1 = 4.5, shape2 = 2)
hist(test_scores, main = "Left-Skewed Distribution", xlab = "Final Exam Score (in %)", col = "lightblue", border = "black")

# Add vertical lines for mean and median
abline(v = mean(test_scores), col = "red", lty = 2, lw = 2)
abline(v = median(test_scores), col = "blue", lty = 2, lw = 2)

# Add legend
legend("topleft", legend = c("Mean", "Median"), col = c("red", "blue"), lty = 2, lw = 2)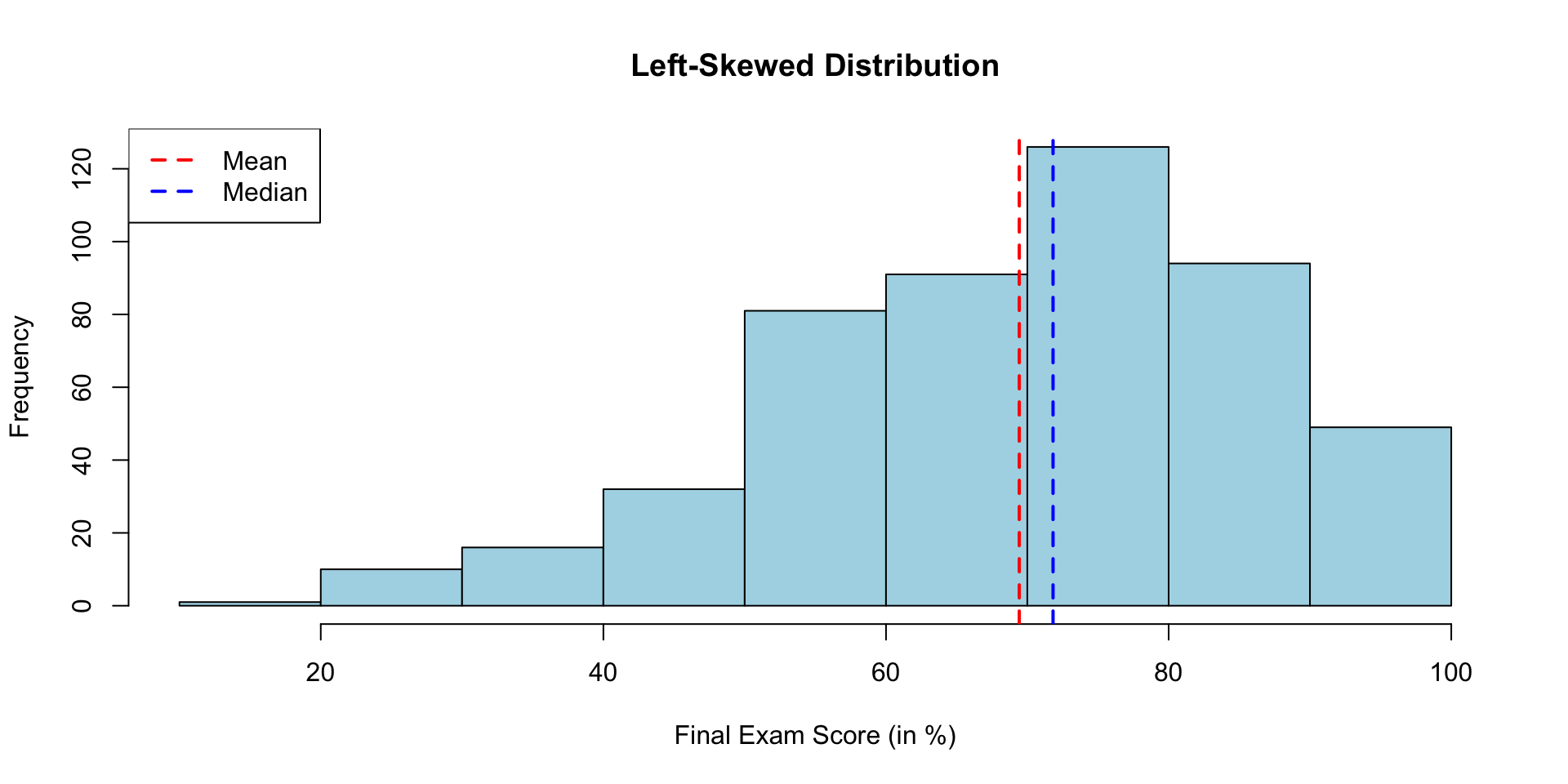

Modality

• Modality describes the number of peaks (modes) in a distribution’s shape. These peaks correspond to local maximums in the frequency or probability density function.

• A distribution can be:

  1. Unimodal: One clear peak (e.g., Normal distribution).
  2. Bimodal: Two distinct peaks (e.g., heights of males and females combined).
  3. Multimodal: More than two peaks.
  4. Uniform: No distinct peaks; the frequency is evenly spread.

Summary

Descriptors for the modality of a distribution

Descriptors for the skewness of a distribution

Quartiles

Quartiles are values that divide a dataset into four equal parts, each representing 25% of the data. There are three quartiles:

1. First Quartile (Q1): Also known as the lower quartile, Q1 represents the 25th percentile of the data. It is the value below which 25% of the data falls.

2. Second Quartile (Q2): is the median of the dataset. It represents the 50th percentile, and 50% of the data falls below and 50% above this value.

3. Third Quartile (Q3): Also known as the upper quartile, Q3 represents the 75th percentile of the data. It is the value below which 75% of the data falls.

Interquartile Range

• The range these data span is called the interquartile range, or the IQR.

\[ IQR = Q3 - Q1 \]

• IQR is a measure of statistical dispersion that describes the spread or variability within the middle 50% of a dataset.

• It is particularly useful when dealing with skewed or non-normally distributed data, as it is less sensitive to extreme values (outliers) than the full range or Standard Deviation.

Boxplot

• A box plot summarizes a data set using five statistics while also plotting unusual observations

• The box in a box plot represents the middle 50% of the data, and the thick line in the box is the median.

You create on in R using:

boxplot(interest_rate)

Whiskers and Outliers

• The so-called whiskers extend from the edges of the box to the minimum and maximum values within a specified range:

\[ [Q_1 - 1.5 \times IQR, Q_3 + 1.5 \times IQR] \]

• Individual data points outside of the range are flagged as suspected outliers and are often plotted individually.

• They can be important to identify because they may indicate unusual observations or errors.

outlier = extreme relative to the rest of the data.

A vertical dot plot, where points have been horizontally stacked, next to a labeled box plot for the interest rates of the 50 loans. Figure 2.10 [@diez2016openintro]

Shape of boxplot

Boxplots can also help to identify skewness:

Variance

Variance

Variance is roughly the average squared deviation from the mean. For a sample of size \(n\) the sample variance¹ is calculated as

\[ s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2 \]

The population variance is given by:

\[ \sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2 \]

square

• gets rid of negatives so that observations equally distant from the mean are weighed equally.
• weighs larger deviations more heavily.

1. The use \(n−1\) in the denominator for the sample standard deviation corrects for the bias in estimating the population standard deviation.

Standard Deviation

• The standard deviation is the square root of the variance

Sample Standard deviation

\[ s = \sqrt{s^2} \]

Population st. deviation

\[ \sigma = \sqrt{\sigma^2} \]

• The standard deviation represents the typical deviation of observations from the mean.

• Standard deviation has the same units as the data.

• The standard deviation is useful when considering how far the data are distributed from the mean.

• The standard deviation is easier to interpret in the context of the original data. For example, if the standard deviation is 5, it means that, on average, individual data points deviate from the mean by about 5 units.

iClicker: Robustness

Robustness

Which measure of central tendency is least affected by extreme values in a dataset?

1. Mean
2. Median
3. Mode
4. Standard Deviation

iClicker: Shape

Tip

Distribution shape

Which of the following best describes the shape of the histogram?

1. right skewed
2. left skewed
3. symmetric
4. uniform

iClicker Boxplot

Boxplot Whiskers

In a boxplot, the whiskers extend to:

1. The minimum and maximum values in the dataset
2. The 25th and 75th percentiles
3. The range defined by \([Q_1 - 1.5 \times IQR, Q_3 + 1.5 \times IQR]\)
4. None of the above

iClicker Modality

Modality

Identify the number of modes (peaks) in the distribution.

1. unimodal
2. bimodal
3. multimodal

A unimodal distribution has one peak, while bimodal or multimodal distributions have two or more peaks.

In order to determine modality, step back and imagine a smooth curve over the histogram – imagine that the bars are wooden blocks and you drop a limp spaghetti over them, the shape the spaghetti would take could be viewed as a smooth curve.

Categorical Data

email

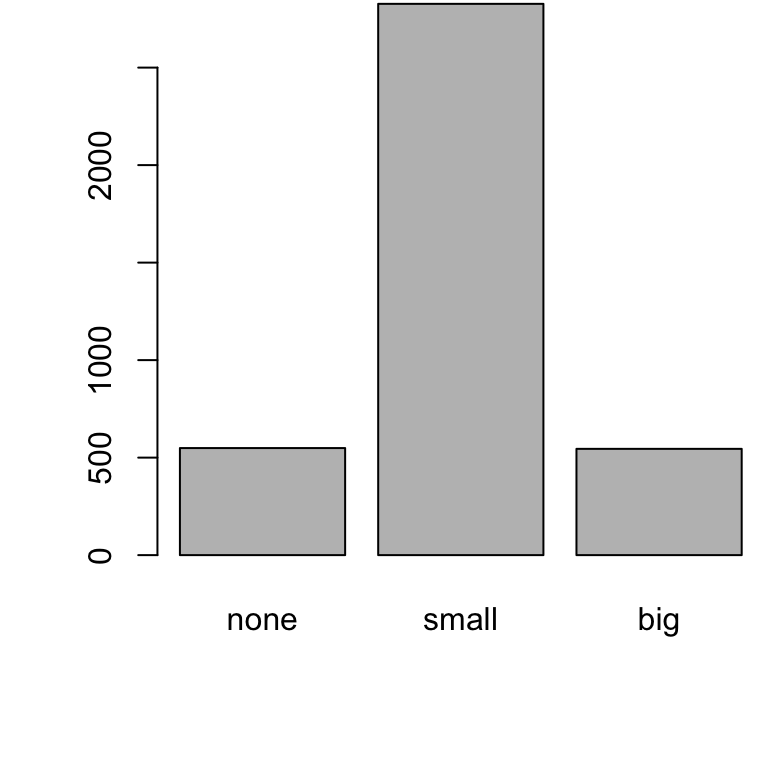
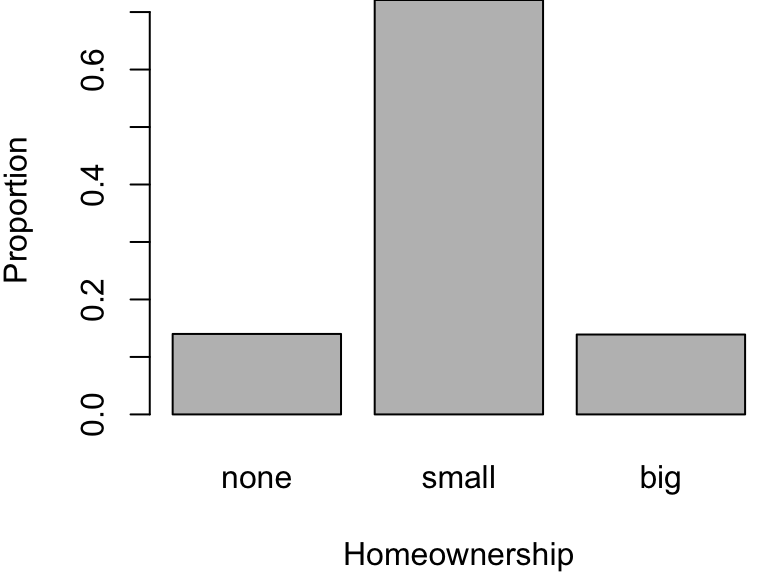
Let’s consider the email dataset which comprise 3921 incoming emails for the first three months of 2012 for an email account (from openintro pacakge):

data(email); email

Frequency Table

A table for a single variable is called a frequency table:

tab <- table(email$number)
tab

 none small   big 
  549  2827   545 

# nicer printout:
knitr::kable(t(tab))

none	small	big
549	2827	545

We can create a barplot in R using barplot(height)¹

barplot(tab)

notice how this is identical to the bottom margin of the contingency table

1. where height is either a vector or matrix of values describing the bars which make up the plot

Bar Plot

A bar plot is a common way to display a single categorical variable.

tab <- table(email$number)
barplot(tab, ylab = "Frequency", 
        xlab = "Homeownership")

We can either plot according to frequency (count) or proportion..

tabTemp <- tab/sum(tab)
barplot(tabTemp, ylab = "Proportion", 
        xlab = "Homeownership")

When proportions instead of frequencies are shown we call this a relative frequency bar plot.

• Bar plots are used for displaying distributions of categorical variables, while histograms are used for numerical variables. The x-axis in a histogram is a number line, hence the order of the bars cannot be changed, while in a bar plot the categories can be listed in any order (though some orderings make more sense than others, especially for ordinal variables.)

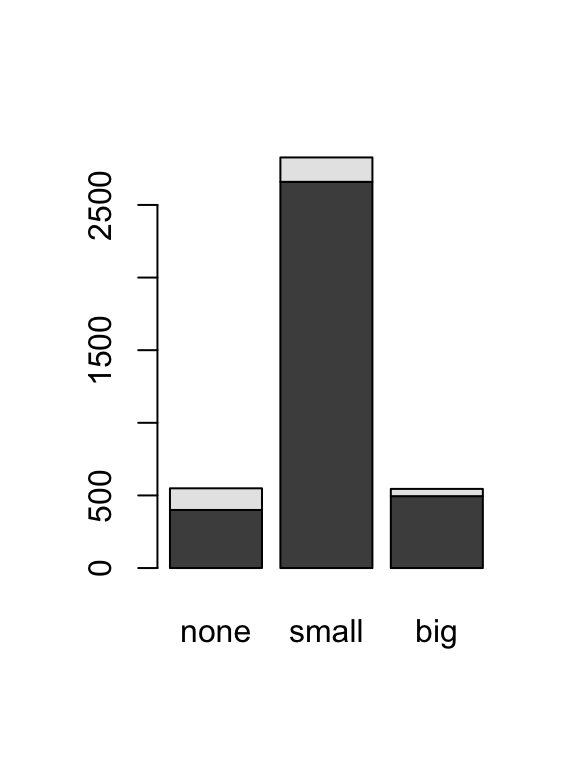
Contingency Tables

• A table that summarizes data for two categorical variables is called a contingency table.

• A contingency table is a tabular representation of the joint distribution of two or more categorical variables.

• e.g. consider the following categorical variables from email:
  • number: what number, if any, is present in the email: none, small (under 1 million), big (a number > 1 million)
  • spam Indicator for whether the email was spam.

email contingency table

(tab <- table(email$spam, email$number))

   
    none small  big
  0  400  2659  495
  1  149   168   50

Stacked Bar plot

tab <- table(email$spam, email$number)

	number
	none	small	big	Total
not spam	400	2659	495	3554
spam	149	168	50	367
Total	549	2827	545	3921

barplot(tab)

Side-by-side bar plot

Alternatively, you may prefer to situate your bars side-by-side rather than stacked. In this side-by-side barplot we have opted to use different colours and create a legend.

# reduce white space in margins
par(mar=c(5.1,4.1,0.1,0.1))

# COL vector from openintro
# see ?COL for details
barplot(tab, beside = TRUE, 
        col = c(COL[1], COL[3]))

# Create a legend
legend("topleft",
  fill = COL[c(1,3)],
  legend = c("not spam", "spam"))

Side-by-side Boxplot

Similarly, it can be useful to look at side-by-side boxplots.

boxplot(
  annual_income~homeownership, 
  data = loan50,
  ylab = "Annual Income")

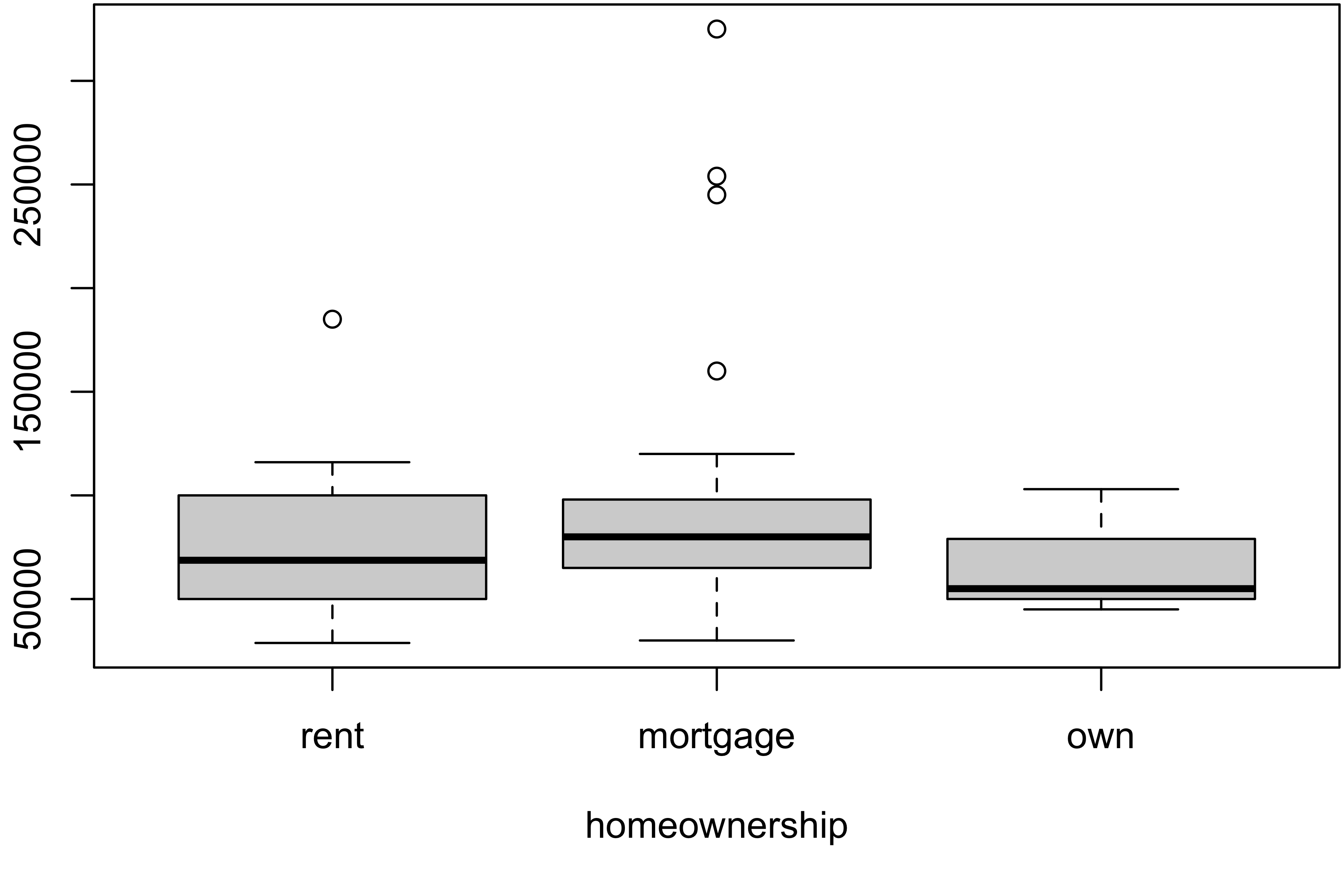
formula notation

The formula notation y ~ x specifies that the variable “y” should be plotted against the levels of the “x” variable.

It suggests that you want to examine the distribution of annual income for different categories of homeownership.

Violin Plots

A violin plot combines the features of a boxplot and the shape of the distribution:

• Shows the distribution of the data across different groups.
• Displays kernel density estimation (don’t worry if you don’t know what that is) on each side, representing the data’s shape.

For some variations on how these can look visit: https://www.sthda.com/english/wiki/ggplot2-violin-plot-quick-start-guide-r-software-and-data-visualization

# Create the violin plot
ggplot(loan50, aes(x = homeownership, y = annual_income)) +
  geom_violin(fill = "lightblue", color = "black") +
  labs(
    title = "Violin Plot of Annual Income by Homeownership",
    x = "Homeownership",
    y = "Annual Income"
  ) +
  theme_minimal()

Figure 1

# Create the stacked histograms
ggplot(loan50, aes(x = annual_income, fill = homeownership)) +
  geom_histogram(binwidth = 10000, color = "black", alpha = 0.7) +
  facet_wrap(~homeownership, ncol = 1, scales = "free_y") +
  labs(
    title = "Histogram of Annual Income by Homeownership",
    x = "Annual Income",
    y = "Count"
  ) +
  theme_minimal()

Figure 2