Lecture 1: Introduction

STAT 205: Introduction to Mathematical Statistics

Dr. Irene Vrbik

University of British Columbia Okanagan

Welcome to STAT 205

Course calendar description [source]:

STAT 205 (3) Introduction to Mathematical Statistics

Sampling distribution theory. Likelihood. Parameter estimation. Confidence intervals and hypothesis testing; simple regression, analysis of variance and contingency table analysis. Credit will be granted for only one of STAT 205 or STAT 230. [3-0-0]. Prerequisite: STAT 203.

• Note the course vector (no labs)
• You should have taken STAT 203

Instructor:

Name: Dr. Irene Vrbik (she/her)

Office: SCI 104

email: irene.vrbik@ubc.ca

Website: irene.vrbik.ok.ubc.ca

Teaching Assistants (TAs):

Name: Ling Xue

A little about me

• I am currently a Tenure-track Assistant Professor of Teaching

• I have taught a variety of courses (from introductory data science and to graduate courses in statistics) at several institutions (Guelph, McGill, MDS Program)

• I am currently the Data Science Program advisor, Articulation, and curriculum representative.

Educational Background

1. McMaster University, BSc (Mathematics & Statistics)

2. University of Guelph, MSc (Applied Statistics)

   Thesis: Using Individual-level Models to Model Spatio-temporal Combustion Dynamics. This involved modelling the spatio-temporal combustion dynamics of fire in a Bayesian framework. Supervisors: Rob Deardon and Zeng Feng.

3. University of Guelph, PhD (Applied Statistics)

   Thesis: Non-Elliptical and Fractionally-Supervised Classification. This involved model-based classification with a particular emphasis on non-elliptical distributions. Supervisor: Paul D. McNicholas.

Experience

Postdoctoral Fellow at McGill University Under the supervision of Dr. David Stephens, this work focused on the statistical and computational challenges associated with analyzing genetic data. It involved clustering and modeling HIV DNA sequences.

Postdoctoral Fellow at UBCO Awarded by NSERC (Natural Sciences and Engineering Research Council of Canada), this research involved collaborations with faculty from several disciplines (eg. Medical Physics, Biology, and Chemistry) and was supervised by Dr. Jason Loeppky.

Instructor at UBCO a three-year contract position in the Department of Computer Science, Mathematics, Physics, and Statistics.

NSERC = is the major federal agency responsible for funding natural sciences and engineering research in Canada.

Research Interests

Statistics and Machine Leaning in Curriculum Design

• e.g. topics modeling in Data Science course calendars

Curricular Analytics the systematic analysis and evaluation of educational curricula to gain insights into various aspects of curriculum design, delivery, and assessment.

• e.g. metric calculation for various pathways, curriculum visualization, course recommendation systems

Tools for teaching, learning, and technology

• e.g. Prairie Learn: online problem-driven learning system for creating homework and tests

Topic Modeling Leverage a class of Bayesian models (Latent Dirichlet Allocation (LDA)) to model pathways through Data Science degrees. Aim to cluster words into latent topics and discover common learning outcomes in Data Science Curricula.

Curricular Analytics Use this information to improve curricula and improve their effectiveness and impact on student learning outcomes. Visualization of curricula as graphs. Metric calculations

Others: tools for teaching, learning, and technology

Course Syllabus

The course syllabus is a dynamic document which has been linked to on Canvas (PDF available for download). Many administrative questions can be answered there:

Course Tools

We will be using Canvas for most course related material:

• Grades
• Assignments (downloading/submitting)
• Course announcements/discussions
• Supplementary files (eg. data sets, code, etc…)

Link to our canvas shell: https://canvas.ubc.ca/courses/135720

note the number at the end

Lecture Format

Lectures will be posted in HMTL format (links on Canvas).

Take time to learn how to:

1. navigate through the slides
2. how to export to PDF
3. annotate¹ and save markings on HTML notes

Should be uploaded shortly before lecture

1. Note that this feature has only been confirmed to work in Google Chrome and Chromium

Lecture format

You will not get the whole story by reading the slides!

• Slides may sometimes be supplemented with handwritten material¹
• Lectures may include R sessions/demos (R scripts will be uploaded to Canvas).
• Lectures may also include discussions which you will only gain access to by attending class.

1. Aside for doodling, substantial written material will be done digitally (on my iPad) and uploaded to Canvas.

Supplementary Reading

• In our course schedule you may notice some suggested reading.

• Unless otherwise specified, these readings are intended to be optional

Programming Language

• Any necessary coding will be done in R:
• Relevant code will be posted to Canvas and embedded in the slides when necessary
• It is also recommended that you complete assignments using Rmarkdown in RStudio.

Clipboard code

A clipboard button appears when you hover over code¹

# R code for calculating Mean and standard deviation

# Create a numeric vector
data <- c(12, 15, 18, 21, 24, 27, 30)

# Calculate mean
mean_value <- mean(data)

# Calculate standard deviation
sd_value <- sd(data)

# Print the results
cat("Mean:", mean_value, "\n")
cat("Standard Deviation:", sd_value, "\n")

Mean: 21 
Standard Deviation: 6.480741 

• If you have a laptop, code along side me if you want!
• Most R content will be discuss in labs, however.
• If viewing in HTML format, you can hover over the code (AKA “R chunk”) for easy copying/pasting.

1. This interactivity will only work on the HTML version of the slides, not PDF.

Why R?

Pros

• exposure to R in Statistics prerequisite course
• Rich Ecosystem
• Reproducibility
• Textbook

Cons

• Steep learning curve
• Performance
• Package Quality
• Limited Industry Adoption

R was developed by statisticians, so it has a strong foundation in statistical modeling and analysis.

R has a vast and comprehensive ecosystem of packages and libraries specifically designed for data analysis, visualization, and statistics.

While R’s primary strength is statistics, it also offers a growing number of machine learning packages, such as caret, randomForest, and xgboost, making it suitable for a variety of data science tasks.

While R is a powerful language for data science, it also has some limitations and drawbacks that you should consider before choosing it for your data science projects. Here are some of the cons of using R for data science:

CONS :

Learning Curve: R has a steeper learning curve compared to some other languages like Python, especially for those who don’t have a strong background in statistics. The syntax can be less intuitive for beginners.

Performance: R can be slower than languages like C++ or Python, particularly when dealing with large datasets or computationally intensive tasks. While there are ways to optimize R code, it may not be the best choice for high-performance computing.

Package Quality: While R has a rich ecosystem of packages, the quality and documentation of packages can vary widely. Some packages may be poorly maintained or lack support, which can lead to compatibility issues and frustration.

Limited Industry Adoption: While R is widely used in academia and certain industries like finance and healthcare, it may not be as prevalent in other sectors. This could impact job opportunities and collaboration with colleagues who use different tools.

R code

• You will be expected to work through any R scripts presented in class or uploaded to Canvas outside of class to ensure you understand the code.

• Since we do not have labs for this course, please ensure that you utilize the office hours to answer any of your questions.

• If you cannot attend my designated office hours, kindly send me your schedule via email, and I’ll arrange an alternative meeting time that suits both of us.

Textbook

We are using an open source textbook available on the UBC Library website:

• Sheldon M. Ross (2021). Introduction to Probability and Statistics for Engineers and Scientists (Sixth Edition), UBC Library link

Other useful textbooks include:

• Devore, J. L., Berk, K. N., Carlton, M. A. (2021). Modern Mathematical Statistics with Applications (3rd edition) UBC Library link

• Ramachandran et. al (2021). Mathematical Statistics With Applications in R (Third Edition) UBC Library link

• Balka, Jeremy. Making Statistics Make Sense. https://www.jbstatistics.com/

• Illowsky, B., Dean, S., Openstax. (2022). Introductory Statistics. Brazil: Open Stax Textbooks.

Class Etiquette

1. Please be respectful, especially to other students
2. Please be present. Attendance will not be taken, but you are encouraged to come and learn together.
3. Please restrict the use of electronic devices to course related material; other content could be distracting.
4. Please be forgiving; instructors are people too, we will make mistakes.

Course Questions

In class

• If you are stuck on a concept during lecture, please feel free to raise your hand and ask for clarification.
• If you are needing help understanding something, chances are, other students are too!
• I will do my best to answer questions on the fly or organize a more thoughtful answer to be presented first thing next class or posted to Canvas.

Course Questions

Outside of class

Outside of class, the general order in which I would suggest you asking course-related questions is:

1. Consult the course syllabus
2. Post your question on the public forum on Canvas*
3. Come see me during Office Hours¹
4. e-mail (weekdays are best)

1. If you cannot attend my designated office hours, kindly send me your schedule via email, and I’ll arrange an alternative meeting time that suits both of us.

Course Questions

About Assignments

If you have any questions about the marking of a question on an assignment

1. First contact your TA directly to inquire on why marks were deducted

2. If you think the question was graded incorrectly/unfairly, please send me an email outlining the problem

Sending emails

1. Be sure to include an email subject that includes the course code¹ and a clear and concise subject line that accurately reflects the content or purpose of your email. Eg.
   • STAT 205: Request for Review: Grading Discrepancy on [Assignment/Question]
2. The body of your email should include your name and student number.

🙏 refrain from sending messages through Canvas and email.

• STAT 205: Request for Meeting to Discuss [Topic]

1. The course code is not needed if you are messaging me through Canvas

STAT 205

Definition of Statistics

What is statistics?

“Statistics is concerned with scientific methods for collecting, organizing, summarizing, presenting, and analyzing data, as well as drawing valid conclusions and making relevant decisions on the basis of such analysis.” ¹

Link to ScienceDirect Topic pages:

• extracts are written by subject matter experts and are drawn from foundational and reference materials such as encyclopedias, journal review articles, monographs, book series and handbooks

• uses machine learning (ML) and natural language processing (NLP) techniques to identify relevant topic-based information from Elsevier’s reference materials to help provide bite-sized and easily digestible introductions to a new subject.

1. Jambu, M. (1991). Exploratory and Multivariate Data Analysis. United States: Elsevier Science.

Applications of Statistics

Statistics is a versatile field that finds applications in almost every discipline and various areas of daily life, e.g.

• Clinical trials: to determine the efficacy of a new drug by comparing outcomes between a treatment group and a control group.
• Sports statistics: batting average of a baseball player
• Government: analyzing census data to allocate government resources and plan infrastructure development.
• Personal finances: analyzing historical financial data to make informed investment decisions
• Health and fitness: Monitoring personal health metrics

discipline, including agriculture, astronomy, biology, business, communications, economics, education, electronics, geology, health sciences,

we interact with statistics every day

Branches of Statistics

Descriptive Statistics

Involves describing, summarizing, and displaying data. For example:

• summary statistics (e.g. average, mode, and standard deviation)
• graphs
• tables, …

Inferential Statistics

Involves using a sample of data to draw conclusions about a population

Source of image: medium.com

Two ways to summarize data are by graphing and by using numbers (for example, finding an average).

We will be talking about both branches or statistics in greater detail throughout the course

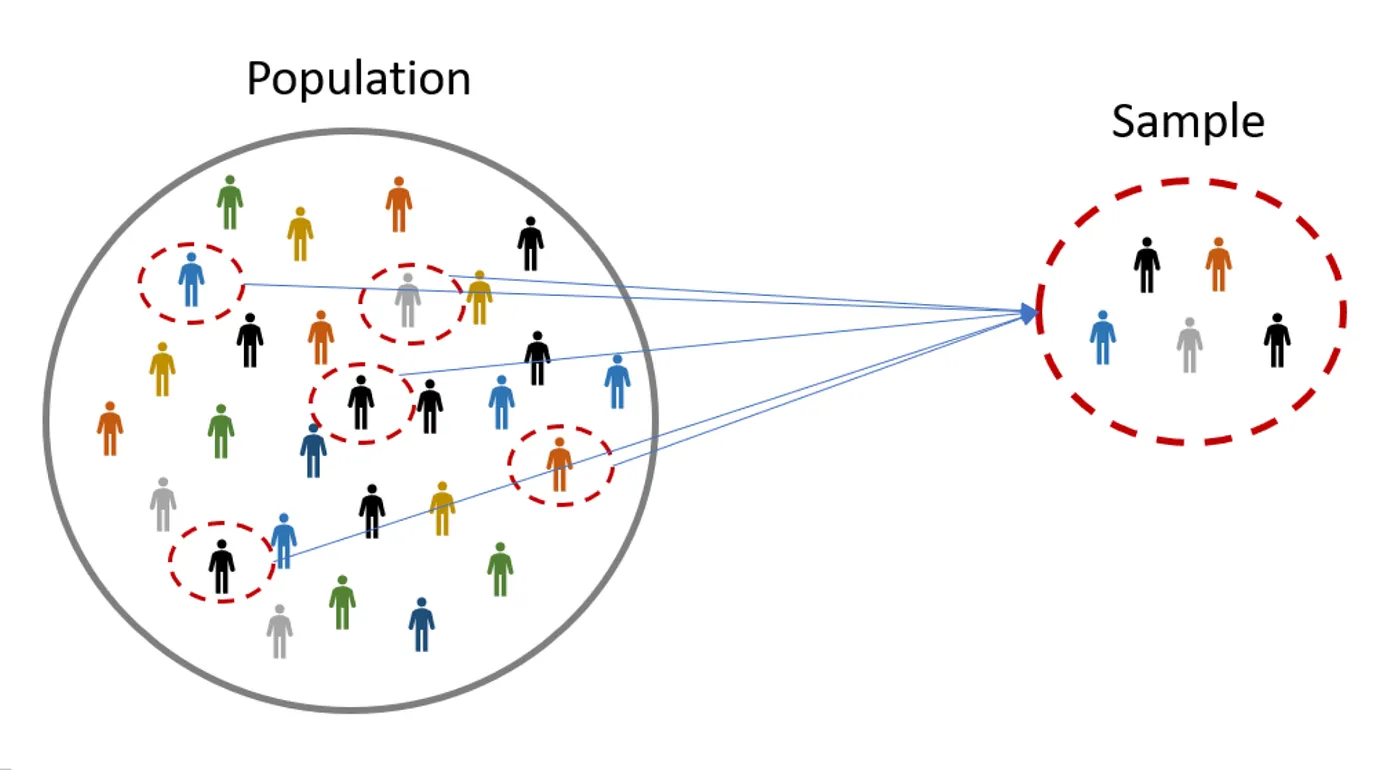
Sampling from a Population

• A sample represents a subset of the cases and is often a small fraction of the population.

• The goal of sampling is to create a subset of the population that is “representative” of the population it is being drawn from.

• We usually denote the size of the population of interest as \(N\)

• A lowercase \(n\) is used to represent the size of a sample from that population.

UBCO Heights Example

• Suppose we were interested in the average height of UBCO students.

• Rather than trying to sample the entire student body, we might take a sample from this population of interest.

• One possible sample could be the height from all of the students in this class …

As we will see this is not a great sample

• only focuses on second-years
• likely students in the data science/math/stat stream

Student Heights

Suppose we had the height of all of the students in this class:

heights

 [1] 173.9 167.6 161.4 173.2 170.1 182.1 168.1 181.5 171.7 171.2 176.8 171.6
[13] 178.4 179.1 170.3 179.4 178.7 177.7 180.8

Descriptive statistics may include, reporting the mean height:

mean(heights)

[1] 174.4

Or ploting the data in a boxplot or histogram:

boxplot(heights)  # output on next slide
hist(heights)     # output on next slide

Student Heights

Left: a boxplot of the class heights. Right: a histogram of the class heights.

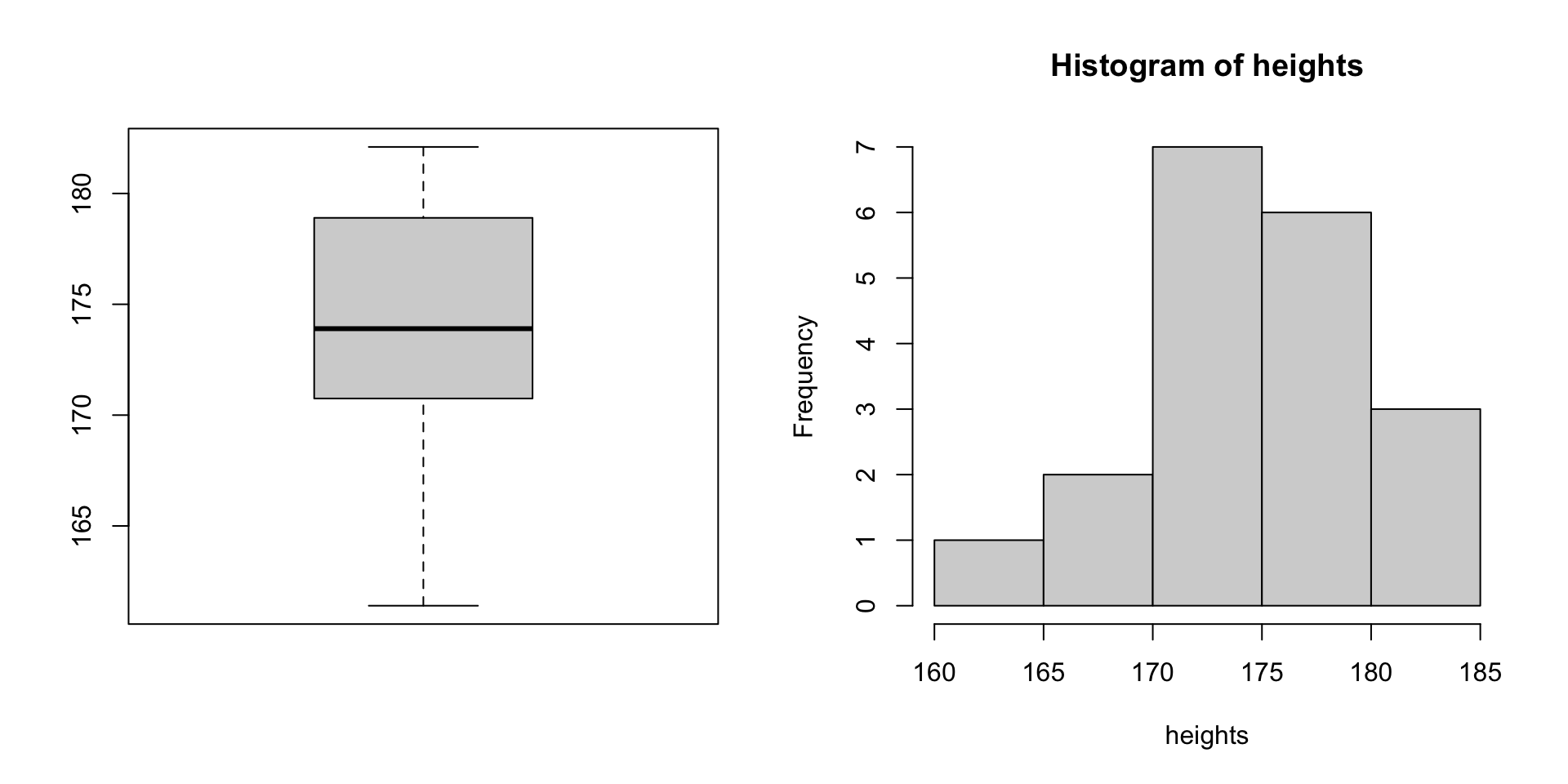
Food for thought

• If we instead sampled heights in a fourth-year Health & Exercise Sciences (HES) course at UBCO, do you think the distribution would look the same?

• A different sample will almost surely produce a different distribution.

• Variation is present in any set of data

• This is something we will return to when we talk about sampling distributions

• Rather than focusing on a single classs, it would be better to take a random sample from a diverse range of students, ensuring a more representative selection of the population.

• Sampling only from second-year data students introduces the risk of selection bias, where the sample may not be representative of the entire student population.
• second-year data students may share certain characteristics or experiences that differ from the broader student body.
• any findings or insights drawn from this sample might not generalize well to the entire student population.

Comparisons of two means

Other questions we might ask could include:

Q: Is the average height of University students at UBCO significantly different that the average height of students at Ohio State University?

Limitations of Statistics

Statistics cannot tell us why relationships or associations exist.

In this course we will be learning about test that can help answer these types of inferential questions.

if we had a sample from each of these University we can answer that question with a hypothesis test

PearUP hypothesis:

• schools with a higher percentage of athletes might have a higher than average height since athletes tend to have an above-average height compared to the general population.

PearUp Research. Where do America’s tallest men go to school medium.com

Research Question

The first step in conducting research is to identify topics or questions that are to be investigated. For example:

1. What is the average mercury content in swordfish in the Atlantic Ocean?
2. Does a new drug reduce the number of deaths in patients with severe heart disease?

Each research question refers to a target population

Target Population

1. What is the average mercury content in swordfish in the Atlantic Ocean?

Population: all swordfish in the Atlantic ocean

2. Does a new drug reduce the number of deaths in patients with severe heart disease?

Population: all patients with severe heart disease

Notice how they are

Limitations of Statistics

Notice that these questions are clear, specific, and address measurable outcomes rather than vague questions like

“What is the impact of technology on society?””

• “impact” and “society” are broad terms that can encompass various aspects.

A better version would be more specific and focused, such as:

“How does the adoption of smartphones affect face-to-face communication patterns among teenagers in urban areas?”

Sampling vs. Census

• At this point you might be wondering why do we collect data from a sample rather than collecting data on the entire target population of interest (i.e. a census)?

• Ideally we would collect data from the entire population of interest; however, sampling methods are employed in statistics for practical, logistical, and financial considerations, …

• national census data: we don’t have a direct role in determining the questions or methods used in these large-scale surveys
• download data from Kaggle

Reasons for sampling

Taking a census may be more complex than sampling

1. Save time and money: Surveying an entire population can be expensive and not feasible within a limited timeframe.

1. It may involve reaching out to every individual, which can be resource-intensive, especially in large populations.

Conducting a full census might not be feasible within a limited timeframe. Sampling allows for quicker data collection

Surveying an entire population can be expensive and time-consuming. Sampling is often more practical and economical.

2. Logistical Challenges: e.g. In cases where the population is geographically dispersed or difficult to reach, sampling provides a more manageable approach.

2. Flight Patterns: Birds are highly mobile and may cover extensive distances during migration. Tracking and collecting data from every individual bird throughout its migratory journey would require sophisticated technology and resources.

there always seem to be some individuals who are hard to locate or hard to measure. And these difficult-to-find people may have certain characteristics that distinguish them from the rest of the population.

3. Infeasibility e.g. it is impossilbe to observe “All people with heart disease” due to a) sheer size b) resource constraints c) logisitcal challenges d) undiagnosed cases

“All people with heart disease”, apart from that population being too large to sample in it’s entirety, some people may not even be diagnosed with heart disease.

Populations rarely stand still. Even if you could take a census, the population changes constantly, so it’s never possible to get a perfect measure

Statistical Inference

• With the right sampling methods, data collected from a subset of the population (a sample) can provide accurate and representative information about the entire population.

• This is the basis of statistical inference.

Statistical Inference

A statistical inference is an estimate, a prediction, a decision, or a generalization about the population based on information contained in a sample.(Ramachandran and Tsokos 2020)

Obtaining good samples

• Almost all statistical methods are based on the notion of implied randomness.

• Most commonly used random sampling techniques are simple¹, stratified² and cluster³ sampling.

• SRS most basic

• equivalent to using a raffle to select cases.

• Stratum: Refers to a single, homogeneous subgroup within a population.

Stratified e.g. students’ academic performance in a university

• Want reflects the diversity of academic disciplines.

• stata = departments (e.g., Engineering, Humanities, Sciences).

• Divide the student body into strata based on academic departments.

• Randomly select a proportionate number of students from each department.

  • If Engineering constitutes 30% of the university’s population, ensure that 30% of your sample is from the Engineering department.

Cluster

Cluster Selection: Randomly select a few departments and survey all students

If observational data are not collected in a random framework from a population, statistical inferences based on these data may not be reliable.

• we wont focus too heavily on these methods
• see: DATA 407 (3) Sampling and Design

1. each case in the population has an equal chance of being included

2. Divide population into stratum and randomly sample from each strata

3. Divide population into clusters, then randomly select clusters

SRS (Simple Random Sampling)

Randomly select cases from the population, where there is no implied connection between the points that are selected. [Source of image (Diez, Barr, and Çetinkaya-Rundel 2016)]

Stratified Sample

Strata are made up of similar observations. We take a simple random sample from each stratum. [Source of image (Diez, Barr, and Çetinkaya-Rundel 2016)]

Cluster Sample

Clusters are usually not made up of homogeneous observations. We take a simple random sample of clusters, and then sample all observations in that cluster. Usually preferred for economical reasons. [Source of image (Diez, Barr, and Çetinkaya-Rundel 2016)]

Obtaining bad samples

Several issues can arise when taking a sample, potentially impacting the validity and reliability of study results.

One way of obtaining a “bad” sample would be to introduce some sort or bias - systematic error or deviation from the true characteristics of the population.

Non-Response Bias: If a significant portion of the selected individuals refuses to participate or cannot be reached, e.g. illegal immigrants

Some Latinos, especially illegal residents, fear that participating in the count will expose them to immigration raids or government harassment.

Selection Bias: occurs when the sampling method favors certain characteristics, leading to an unrepresentative group, e.g. technology-based health interventions

• in order to participate in this study you needed access to the internet (web-based messaging portal)

• can lead to skewed results that do not accurately reflect the entire population.

• Excluded patients were older, less educated, less engaged and activated in their health, lower socioeconomic status [SES] and had worse health (ie, more medical comorbidities) than nonexcluded patients.

• sampling the first 50 people in the building to ask them about their commute time

The Literary Digest Poll

• The Literary Digest polled about 10 million Americans, and got responses from about 2.4 million.
• The poll showed that Alf Landon of Kansas would likely be the overwhelming winner and Franklin D. Roosevelt (FDR) would get only 43% of the votes.

• Election result: FDR won, with 62% of the votes.
• The magazine was completely discredited because of the poll, and was soon discontinued.

• presidential election, incumbent Democratic President Franklin D. Roosevelt
• winning with the fourth-largest electoral vote margin in American history.

What went wrong?

• The magazine had surveyed its own readers who had registered automobile and registered telephones.

• These groups had incomes well above the national average of the day (remember, this is Great Depression era) which resulted in lists of voters far more likely to support Republicans than a truly typical voter of the time.

• In other words the sample was not representative of the American population at the time.

Large samples are preferable, but…

• The Literary Digest election poll was based on a sample size of 2.4 million, which is huge, but since the sample was biased, the sample did not yield an accurate prediction.

Example: University Height

Imagine you want to determine the average commute time of employees working in a large office building. Instead of collecting data from each of the 3,500 people working in the building, you randomly select a sample of 100 employees from different departments and floors.

What is \(N\)? 3500

What is \(n\)? 100

Achieving a “representative” sample is crucial in ensuring that the characteristics of the sample accurately reflect those of the entire population.

Back to the height example, we wouldn’t want to have it so that our 100 samples came from members of the varsity basketball team for example ..

Q: Do you think sampling the first 100 people who arrive at the building would be a suitable sampling approach?

No. This sample is not representative of the entire population,

People who arrive early may have different characteristics (e.g., shorter commute times, higher job commitment) compared to the overall employee population.

Data Basics

Source: (Diez, Barr, and Çetinkaya-Rundel 2016) Figure 1.7

• a variable is a characteristic or attribute that can take on different values.

• let’s define the common data types, which is important for determining how we can analyze our data.

• First, we have numeric, or quantitative data two subtypes:

  • Continuous data is measured on a continuous scale, taking any value, such as stock price. We also have
  • interval, or count data. These are measured in whole numbers, such as counting how many cups of coffee people drink per day.

Categorical (Qualitative) Variables: Represent categories or groups and can be further classified as nominal (categories with no inherent order) or ordinal (categories with a specific order).

• order, strongly disagree, disagree, neutral, etc.
• no-order, eye-colour

Classroom Survey

A survey was conducted on students in an introductory statistics course. Below are a few of the questions on the survey, and the corresponding variables the data from the responses were stored in:

• gender: What is your gender?
• intro_extra: Are you an introvert or an extrovert?
• sleep: How many hours do you sleep at night, on average?
• bedtime: What time do you usually go to bed?
• countries: How many countries have you visited?
• dread: On a scale of 1-5, how much do you dread being here?

Data Matrix

Data collected on students in a statistics class on a variety of variables.

a variable is a characteristic or attribute that can take on different values.

• observation - the formal name for a row is a case or observational unit.

Types of variables

• gender: categorical
• intro_extra:categorical

• sleep: numerical, continuous
• bedtime: categorical, ordinal
• countries: numerical, count
• dread: categorical, ordinal - could also be treated as numerical

Associated vs. independent

• When two variables show some connection/relationship with one another, they are called associated (or dependent) variables.

• If two variables are not associated, i.e. there is no evident connection between the two, then they are said to be independent.

Positive Association

Based on the scatterplot above the head length and skull width or possus are positively associated

Relationships among variables

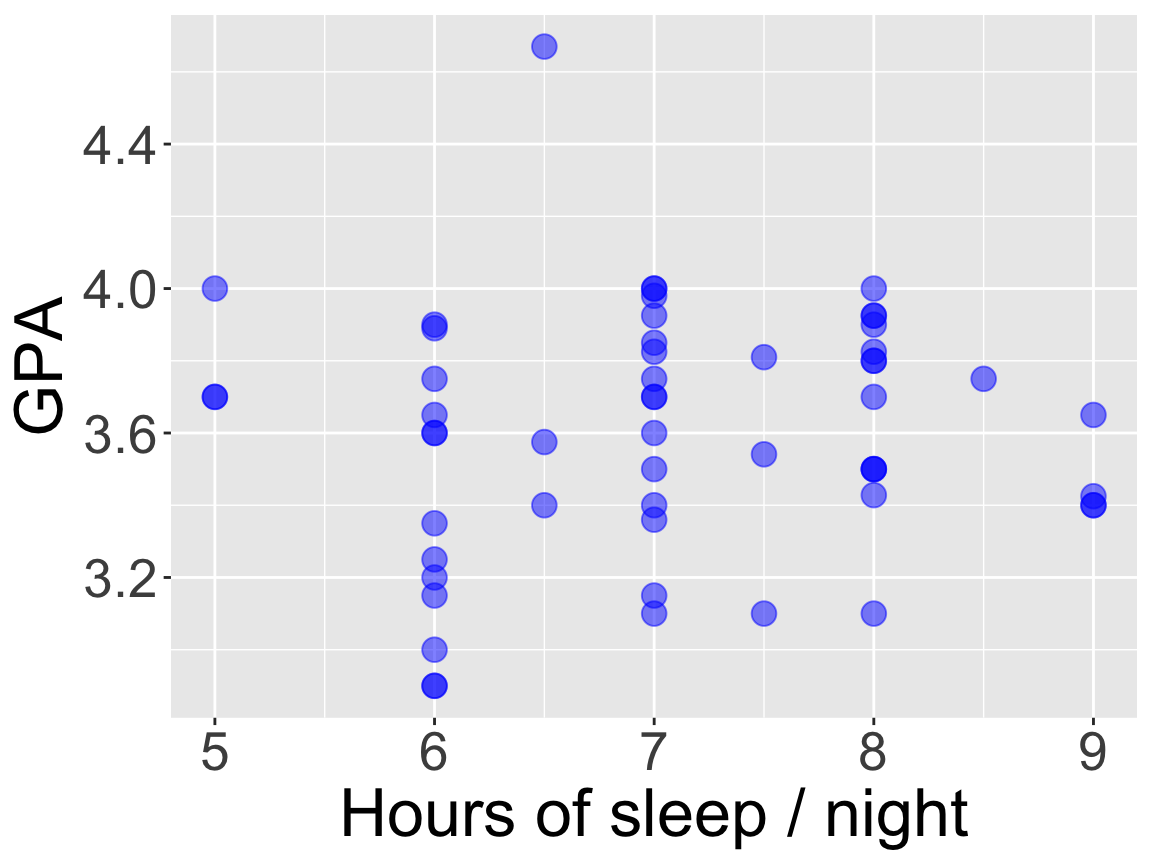
Does there appear to be a relationship between the hours of sleep per night and the GPA of a student?

Q: Do you spot anything unusual about these data points?

looks like gpa independent of hours sleep

Outliers

Statistical methods or visualizations can be used to detect values that deviate substantially from the overall pattern.

Outliers are data points that significantly differ from the rest of the data in a dataset. This can be caused by measurement errors, data entry (human error), natural variation, or genuine anomalies (novelties in data).

Outliers can distort statistical analyses and models, influencing results and interpretations. Treatment include removal, transformation, or employing robust statistical methods.

Causes - Measurement errors, natural variation, or genuine anomalies can lead to outliers.

Handling Outliers Options include removal, transformation, or employing robust statistical methods.

Observational Study

• There are two primary types of data collection: observational studies and experiments.

• In some observational studies data is collected in a way that does not directly interfere with how the data arise.

• In general, observational studies can provide evidence of a naturally occurring association between variables, but they cannot by themselves show a causal connection.

e.g. surveys results, review medical or company records, or follow a cohort of many similar individuals to form hypotheses about why certain diseases might develop.

In each of these situations, researchers merely observe the data that arise.

• Results of an observational study can generally be used to establish an association between the explanatory and response variables.

Experiments

• When researchers want to investigate the possibility of a causal connection, they conduct an experiment.

• In an experiment a researcher manipulates one or more independent variables to observe their effect on a dependent variable while controlling other relevant factors.

When we suspect one variable might causally affect another, we label the first variable the explanatory variable and the second the response variable.

\[ \text{explanatory variable} \xrightarrow{\text{might affect}} \text{response variable} \]

Closing Remarks

• Proficiency in R facilitates the execution of calculations, but true statistical analysis requires interpretation, critical thinking, and the ability to choose and apply appropriate methods in diverse contexts.

• Overall, a solid understanding of statistics empowers individuals across diverse fields to make more rational, evidence-based decisions, contributing to both personal and professional success.

• Statistics is an applied field with a wide range of practical applications. • You don’t have to be a math guru to learn from real, interesting data. • Data are messy, and statistical tools are imperfect. But, when you understand the strengths and weaknesses of these tools, you can use them to learn about the world.

References

Diez, D. M., C. D. Barr, and M. Çetinkaya-Rundel. 2016. OpenIntro Statistics. OpenIntro, Incorporated. https://books.google.ca/books?id=wfcPswEACAAJ.

Ramachandran, K. M., and C. P. Tsokos. 2020. Mathematical Statistics with Applications in r. Elsevier Science. https://books.google.ca/books?id=t3bLDwAAQBAJ.