Lecture 7: Hypothesis Testing one-sample mean

STAT 205: Introduction to Mathematical Statistics

Dr. Irene Vrbik

University of British Columbia Okanagan

Motivation

• Estimating a parameter from sample data can involve:

  • A single number (a point estimate).

  • An interval of plausible values (a confidence interval).

• Often, the goal of an investigation isn’t just parameter estimation, but deciding between two contradictory claims about the parameter.

• This fall under statistical inference, specifically hypothesis testing.

Learning Objectives

• Understand the concept of hypothesis testing for a population mean.
• Formulate null and alternative hypotheses.
• Compute the test statistic and p-value.
• Interpret results in context.

Outline

In this lecture we will be covering

Terminology:

• Null/Alternative Hypotheses

• Significance Level (\(\alpha\)-level)

• Critical Value

• Test Statistic

• Rejection Region (RR)

Approaches:

• Critical Values

• \(p\)-value(next lecture)

What is a hypothesis test?

A statistical hypothesis, or just hypothesis, is a claim or assertion either about

• the value of a single parameter (e.g. \(\mu\) = 50)

• characteristic of a population (e.g. the population is normally distributed)

• about the values of several parameters, (e.g \(\mu_{smokers} = \mu_{non-smokers}\))

Today we’ll be focusing on hypothesis testing for single parameters

1. A battery manufacturer claims that the average battery life of their product is 50 hours. \[ \begin{align} \mu &= 50 \text{ hours} & \mu&\neq 50 \text{ hours} \end{align} \]

2. A medical researcher wants to compare the average blood pressure levels between two groups (smokers vs. non-smokers).

In any hypothesis-testing problem, there are two contradictory hypotheses under consideration.

null means “of no value, effect, or consequence,”

\(H_0\) = the hypothesis of no change (from current opinion), no difference, no improvement.

Null Hypotheses

Definition 1 A null hypothesis (\(H_0\)) represents the status quo or a claim to be tested, often stating that the population mean equals a specific value.

Alternative Hypothesis

Definition 2 The alternative hypothesis (\(H_A\) or \(H_a\) or \(H_1\)) represents an alternative claim and suggests a difference from the null hypothesis, often represented by a range of possible parameter values.

Objective: based on sample information, decide which of the two hypotheses is most likely.

\(H_a\) as the research hypothesis since it is the claim that the researcher would really like to validate.

Battery Life

Exercise 1 A battery manufacturer claims that the average battery life of their product is 50 hours.

Null Hypothesis

\(\mu = 50\) hours

Alternative Hypothesis

\(\mu \neq 50\) hours

Forms of Alternative Hypothesis

For a one-sample with \(H_0: \theta = \theta_0\), our alternative hypothesis can take one of the following forms:

Two-tailed test	\(H_A: \theta \neq \theta_0\)
Left-tailed test	\(H_A: \theta < \theta_0\)
Right-tailed test	\(H_A: \theta > \theta_0\)

Hypothesized value

\(\theta_0\) represents the null value (aka hypothesized value) of the population parameter \(\theta\). It practice this will be some specific value based on prior knowledge, historical data, claims, or assumptions about the population parameter.

Voter Turnout in Santa Clara County (iClicker)

Exercise 2 We want to test whether the proportion of registered voters in Santa Clara County who voted in the primary election is more than 30%. Which of the following correctly represents the null and alternative hypotheses?

1. \(H_0: p = 0.30\), \(H_A: p < 0.30\)
   
2. \(H_0: p = 0.30\), \(H_A: p > 0.30\)
   
3. \(H_0: p \neq 0.30\), \(H_A: p = 0.30\)
   
4. \(H_0: p > 0.30\), \(H_A: p = 0.30\)

Average College Duration (iClicker)

Exercise 3 We want to test whether college students take less than five years on average to graduate. Which of the following correctly represents the null and alternative hypotheses?

1. \(H_0: \bar X = 5\), \(H_A: \bar X < 5\)
   
2. \(H_0: \bar x = 5\), \(H_A: \bar x < 5\)
   
3. \(H_0: \mu < 5\), \(H_A: \mu = 5\)
4. \(H_0: \mu = 5\), \(H_A: \mu < 5\)
   

Key Takeaways

• The null hypothesis (\(H_0\)) always\(^*\) includes an equal sign because it represents the assumed or claimed value of the population parameter that we are testing.

• The alternative hypothesis \(H_A\) is what we want to investigate and is based on the research question. It points in the direction of the suspected difference.

• Both hypotheses must be written in terms of the population parameters

Key Principles of Hypothesis Testing

In statistics, hypothesis-testing problems are formulated so that the null hypothesis is initially assumed to be true.

• \(H_0\) will be rejected in favor of \(H_1\) if the sample data provides strong enough “evidence” (we’ll get back to this).

• If there is insufficient evidence, we fail to reject \(H_0\), meaning we do not have enough support for \(H_A\).

Important

Failing to reject \(H_0\) but this does not prove \(H_0\) ​is true—only that we lack strong evidence against it.

TikTok Watching Habits

Exercise 4 (Tiktok) A social media research group claims that the average number of TikTok videos watched per session is 35 videos. However, a digital well-being organization suspects that people are actually watching more than that per session, contributing to increased screen time. To investigate, the organization collects data from 25 randomly selected TikTok users and finds that they watch an average of 38 videos per session. From past research, the population standard deviation is known to be \(\sigma\) = 6 videos.

\[ \begin{align} H_0: \quad \quad\quad \quad\quad \quad \quad \quad\quad \quad & H_1:\quad \quad\quad \quad\quad \quad \end{align} \]

Even if this null hypothesis is true, we don’t expect \(\bar x\) to be exactly 35.

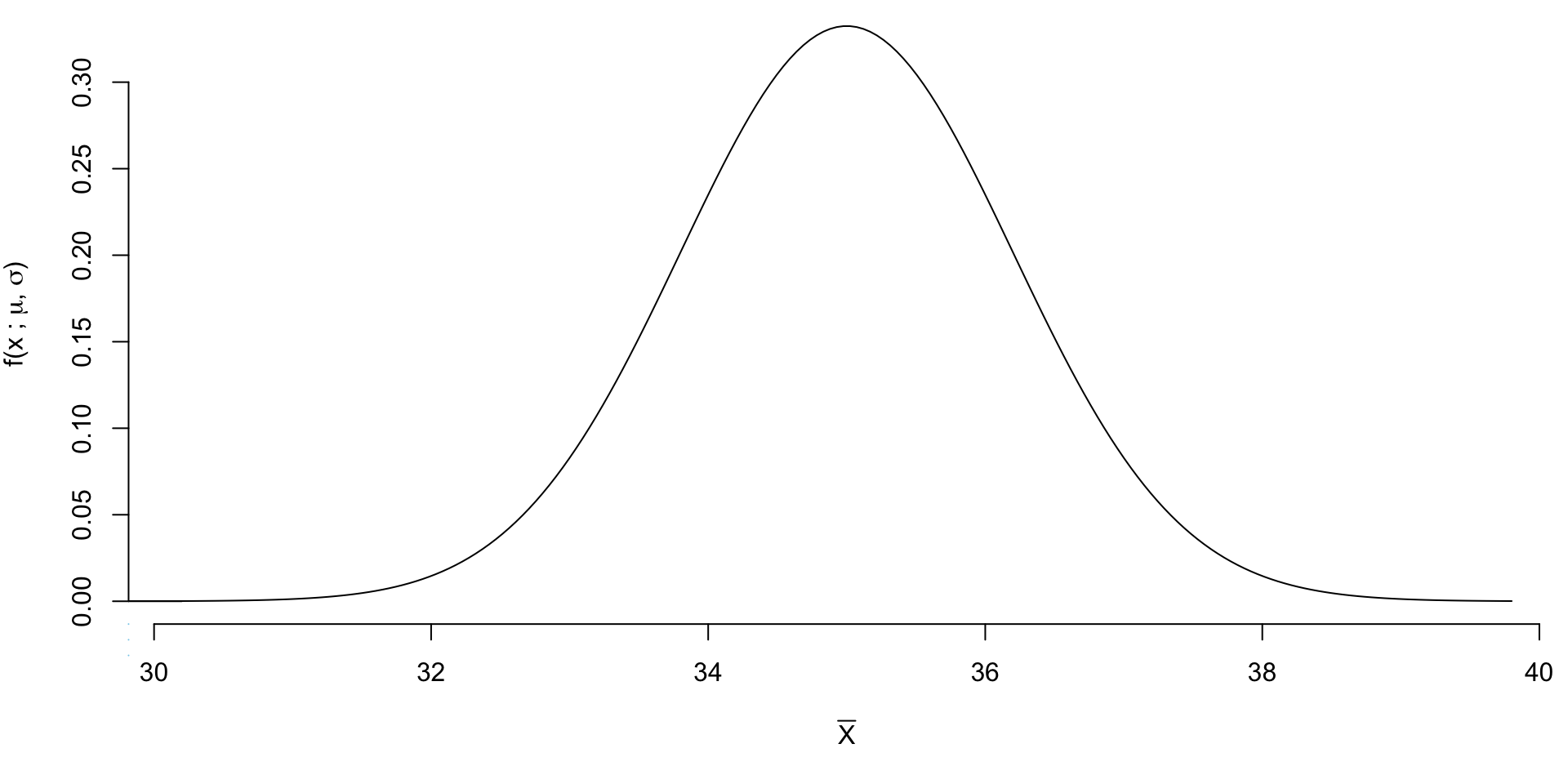
If \(H_0: \mu = 35\) is true and \(\sigma = 6\), we know that \(\bar X \sim N(\mu_\bar{X} = 35, \sigma_\bar{X} = 6/\sqrt{25})\)

If our sample of size 25 produced a sample mean of 34.9, that would be pretty consistent with our null (\(H_0: \mu = 35\)).

If our sample of size 25 produced a sample mean of 35.1, that would be pretty consistent with our null (\(H_0: \mu = 35\)).

If our sample of size 25 produced a sample mean of 36.2, we might consider that a reasonably likely to happen under the null (\(H_0: \mu = 35\)).

If our sample of size 25 produced a sample mean of 37, we might start questining the initial claim (\(H_0: \mu = 35\)).

If our sample of size 25 produced a sample mean of 40, we might stop believing the claim (\(H_0: \mu = 35\)) altogether.

So what would be a reasonably cutoff for separating the unlikely values (that would lead us to reject \(H_0\)) from the values we deem are likely to have occured by random chance?

How big a sample size would we have to observe before we no longer beleive the null and start to favour my alternative hypothesis

Notation

Critical Value

Definition 3 A critical value is a threshold that defines the boundary for rejecting the null hypothesis (\(H_0\)​) in a hypothesis test. It is based on the significance level (\(\alpha\)) and the sampling distribution of the test statistic.

Significance Level

Definition 4 The significance level, denoted by \(\alpha\), represents the probability of rejecting \(H_0\) when it is true. Common¹ choices: \(\alpha = 0.05\) (our course default), \(\alpha = 0.01\)

1. unless otherwise specified, you may assume \(\alpha = 0.05\)

Cutoff

qnorm(0.05, mean = 35, sd = 6/sqrt(25), lower.tail = FALSE)

[1] 36.97382

Using \(\alpha = 0.05\) our critical value becomes 36.974.

Critical Value

qnorm(0.05, lower.tail = FALSE)

[1] 1.644854

Figure 1: Alternatively, we find the critical value on the standard normal.

Critical Value using Tables

Need \(z\) such that

\[ \begin{align} \Pr(Z > z) & = 0.05\\ \implies \Pr(Z \leq z) &= 0.95\\ \end{align} \]

Since it falls between two values, we take the average

\[ \begin{align} \Pr(Z < 1.64) &= 0.945\\ \Pr(Z < 1.65) &= 0.505\\ \implies \Pr(Z < 1.645) &\approx 0.505 \end{align} \]

We want to find the \(z\) value such that \(\Pr(Z > z) = 005\)

Since the \(Z\)-table gives the area to the left of a given \(z\)-score, we need to look up 1 - \(\alpha\) = 0.95.

Test Statistic

Since we assume \(\sigma\) is known, and we assume \(\mu = \mu_0\) (the hypothesized value) we can standardize \(\bar{x}\) using a Z-score transformation. This is called our test statistic.

\[ Z = \dfrac{\bar X - \mu_0}{\sigma/\sqrt{n}} \sim N(0,1) \] \(Z_{obs}\) is the observed test statistic obtained by subbing \(\bar x\) for \(\bar X\).

Test Statistic

Definition 5 A test statistic, a function of the sample data on which the decision (reject \(H_0\) or do not reject \(H_0\)) is to be based. It is typically calculated as:

\[ \begin{align} \text{Test Statistic} &= \dfrac{\text{Point Estimate - Hypothesized value} }{\text{Standard error of Point Estimator}}\\ &= \frac{\hat \theta - \theta_0}{\sigma_{\hat \theta}} \end{align} \]

Null Distribution

Definition 6 The null distribution is the probability distribution of a test statistic under the assumption that the null hypothesis (\(H_0\)) is true.

Rejection Region

Reject if \[ \begin{align} &z_{obs} \geq z_{\alpha}\\ &z_{obs} \geq 1.645 \\ \end{align} \]

The rejection region (also called the critical region or RR for short) is the set of values for the test statistic that leads to reject the null hypothesis (\(H_0\)) in favour of the alternative (\(H_A\)). It is determined based on the chosen significance level (\(\alpha\)).

Acceptance Region

Fail to reject if

\[ \begin{align} &z_{obs} < z_{\alpha}\\ &z_{obs} < 1.645 \\ \end{align} \]

The acceptance region (also called the non-rejection region) is the set of values for the test statistic where we fail to reject the null hypothesis (\(H_0\)). It is the complement of the critical region and represents outcomes that are not extreme enough to provide sufficient evidence against \(H_0\) at the given significance level (\(\alpha\)).

One sided (Right-tailed)

\[ \begin{align} H_0: \mu &= \mu & H_0:& \mu > \mu \end{align} \]

Upper-tailed: Illustration of the hypothesis test for \(H_0: \mu = \mu_0\) versus \(H_A: \mu > \mu_0\). The null distribution follows a standard normal curve. The rejection region (red) corresponds to values where \(H_0\) is rejected at significance level \(\alpha\), while the acceptance region (green) includes values where \(H_0\) is not rejected. The critical value \(z_\alpha\) separates these regions

One Sided (Left-tailed)

\[ \begin{align} H_0: \mu &= \mu & H_0:& \mu < \mu \end{align} \]

Lower-tailed: Illustration of the hypothesis test for \(H_0: \mu = \mu_0\) versus \(H_A: \mu < \mu_0\). The null distribution follows a standard normal curve. The rejection region (red) corresponds to values where \(H_0\) is rejected at significance level \(\alpha\), while the acceptance region (green) includes values where \(H_0\) is not rejected. The critical value \(z_\alpha\) separates these regions

Two-sided

Double-sided: Illustration of the hypothesis test for \(H_0: \mu = \mu_0\) versus \(H_A: \mu \neq \mu_0\). The null distribution follows a standard normal curve. The rejection region (red) corresponds to values where \(H_0\) is rejected at significance level \(\alpha\), while the acceptance region (green) includes values where \(H_0\) is not rejected. The critical values \(-z_{\alpha/2}\) and \(z_{\alpha/2}\) separates these regions

Two-sided Rejection Region

Reject if

\[ \begin{align} | z_{obs} | &> z_{\alpha/2}\\ | z_{obs}| &> ? \\ \end{align} \]

Double-sided: Illustration of the hypothesis test for \(H_0: \mu = \mu_0\) versus \(H_A: \mu \neq \mu_0\). The null distribution follows a standard normal curve. The rejection region (red) corresponds to values where \(H_0\) is rejected at significance level \(\alpha\), while the acceptance region (green) includes values where \(H_0\) is not rejected. The critical values \(-z_{\alpha/2}\) and \(z_{\alpha/2}\) separates these regions

Finding the Critical Value (iClicker)

Exercise 5 A two-tailed hypothesis test is conducted at a significance level of \(\alpha = 0.05\). The test statistic follows a standard normal distribution. What is the critical value \(z_{\alpha/2}\) that defines the rejection regions?

1. \(z_{0.05} = 1.645\)
   
2. \(z_{0.025} = 1.96\)
   
3. \(z_{0.01} = 2.33\)
   
4. \(z_{0.005} = 2.58\)

Answer:

Test Procedure using a significance level of \(\alpha\)

1. State the null and alternative hypotheses \[ \begin{align} H_0: \mu &= \mu_0 & H_1: & \begin{cases} \mu < \mu_0\\ \mu > \mu_0 \\ \mu \neq \mu_0 \end{cases} \end{align} \]

2. Compute \(Z_{obs} = \dfrac{\bar x - \mu_0}{\frac{\sigma}{\sqrt{n}}}\)

3. Determine the Critical Value; see Figure 2

4. Make a Decision

• reject \(H_0\) if \(z_{obs}\) falls in the RR
• fail to reject \(H_0\) if \(z_{obs}\) falls outside the RR

5. State the Conclusion

Figure 2: Illustration of the critical values as determined by the significance level (\(\alpha\)) and the statistical test being used.

TikTok Watching Habits Revisited

A social media research group claims that the average number of TikTok videos watched per session is 35 videos. However, a digital well-being organization suspects that people are actually watching more than that per session, contributing to increased screen time. To investigate, the organization collects data from 25 randomly selected TikTok users and finds that they watch an average of 38 videos per session. From past research, the population standard deviation is known to be \(\sigma\) = 6 videos.

Using a significance level of \(\alpha\) =0.05, conduct a hypothesis test to determine whether there is enough evidence to conclude that users are watching more than 35 videos per session.

Solution

1. State the null and alternative hypothesis

\[ \begin{align} H_0: \mu &= 35 \quad \quad & H_1: \mu &> 35 \end{align} \]

2. Test statistic \(z_{obs} = \dfrac{\bar x - \mu_0}{\frac{\sigma}{\sqrt{n}}} = \dfrac{38 - 35}{\frac{6}{\sqrt{25}}} = 2.5\)

3. Determine the Critical Value

   qnorm(alpha, lower.tail = FALSE)

   [1] 1.644854

4. Make a Decision

• Since \(z_{obs}\) falls in the rejection region, we reject the null hypothesis OR
• Since \(z_{obs} > z_{\alpha}\), we reject the null hypothesis

5. State the Conclusion

• There is statistically significant evidence to conclude that users watch more than 35 TikTok videos per session on average.

Decision Visualized