Sampling Distribution of the Sample Mean

STAT 205: Introduction to Mathematical Statistics

Dr. Irene Vrbik

University of British Columbia Okanagan

Outline

\(\newcommand{\Var}[1]{\text{Var}({#1})}\)

In this lecture we will be covering

• Sampling Distribution of the mean

• Central Limit Theorem

• Examples in action

Introduction

• Based on the probabilistic foundations covered in STAT 203, this lecture will cover a fundamental concept in statistics that describes the behavior of the sampling distribution.

• Statistical inference aims to draw meaningful and reliable conclusions about a population based on a sample of data drawn from that population.

🤔 What is a “statistic”?

Statistics Timothee Chalamet GIFfrom Statistics GIFs

Recall:

Definition: (Sample) Statistic

Let’s denote the sample data as \(X = (X_1, X_2, \dots, X_n)\) , where \(n\) is the sample size. A statistic, denoted \(T(X)\), is a function of a sample of observations.

\[ T(X) = g(X_1, X_2, \dots, X_n) \]

Probability Distribution

A probability distribution is a function showing the likelihood of all possible outcomes for a random variable.

Random Sample

Definition: Sample

If \(X_1, X_2, \dots, X_n\) are independent random variables (RVs) having a common distribution \(F\), then we say that they constitute a sample (sometimes called a random sample) from the distribution \(F\).

• Oftentimes, \(F\) is not known and we attempt to make inferences about it based on a sample.
• Parametric inference problems assume \(F\) follows a named distribution (e.g. normal, Poisson, etc) with unknown parameters.

for instance, one might suppose that F was a normal distribution function having an unknown mean and variance

Capital letters, e.g. \(X\), imply RVs, i.e. they have not been observed yet. Lower case letters, e.g. \(x\), imply observed values for the corresponding RV \(X\).

Sample Mean

A prime example of a statistic is the sample mean

\[ \bar X = \dfrac{X_1 + X_2 + \dots + X_n}{n} \]

At the end of the day, \(\bar X\) is just another random variable, and therefore has its own probability distribution.

Rather than recalling the theorem right away, let’s explore it empirically using a simulation.

\(\bar X\) so it will have a mean (expecte value) and variance

what are the likely values that \(\bar X\) can take on, how likely is each value or inteval of values

Today we focus on the sample mean, but we will look at other sample statistics like the sample proportion and sample variance later in the course.

Example: loan* data

• Let’s return to our loan50 example from previous lectures.

• This data set represents 50 loans made through the Lending Club platform, which is a platform that allows individuals to lend to other individuals.

library(openintro)
data("loan50")             # data from last lecture
data("loans_full_schema")  # full data 

loan50 just 50 observations

loans_full_schema has 10,000 obs

Population data

• The loans_full_schema comprise 10,000 loans made through the Lending Club platform.

• Let’s pretend for demonstration purposes that this data set makes up all the loans made through the Lending Club and thus represents the population.

• loan50 is therefore a sample from that population.

Histogram: Population vs Sample

For the population we might be interested in some parameter, for example, the average loan amount, i.e. the mean value \(\mu\), and its standard deviation \(\sigma\).

Parameters

Population

The population mean is not usually possible to compute, but since we have the data for the entire population we can easily calculate it using:

mu = mean(loans_full_schema$loan_amount)
sigma = sd(loans_full_schema$loan_amount)

There average loan amount is

\(\quad\mu\) = $16,361.92

The standard deviation is

\(\quad\sigma\) = $10,301.96

Sample

If we did not have access to the population information (as is often the case) and instead only had access to a sample, we would instead compute the sample mean:

xbar = mean(loan50$loan_amount)
sample_sd = sd(loan50$loan_amount)

There sample average loan amount is

\(\quad\bar x\) = $17,083.00

The sample standard deviation is

\(\quad s\) = $10,455.46

Random Samples in R

2🎲 A different sample of 50 will produce a different estimate:

N = nrow(loans_full_schema) # 10,000 observations
# randomly sample 50 rows:
sampled50_loans <- loans_full_schema[sample(N, 50), ]
# calculate the average loan amount from sample
mean_loan_amount <- mean(sampled50_loans$loan_amount)

[1] $15,745.00

3🎲 If we do it again, we get yet another (different) estimate:

sampled50_loans <- loans_full_schema[sample(N, 50), ]
mean_loan_amount <- mean(sampled50_loans$loan_amount)

[1] $16,183.00

In repeated sampling the value of the sample mean would vary from sample to sample.

So how do we correct for this discrepency?

• none of the sample estimates are exactly right
• each sample leads us to a different answer

Sampling Distribution of the mean

Let’s repeat this process many times and keep track of all of the sample mean calculations (one for each sample).

mean_vec = NULL 
for (i in 1:1000) {
  sampled50_loans <- loans_full_schema[sample(N, 50), ]
  mean_vec[i] <- mean(sampled50_loans$loan_amount)
}
mean_vec[1:20]

 [1] 15564.0 14651.5 16365.5 17454.5 15201.0 16241.0 17368.0 15622.5 17349.5
[10] 16319.0 15689.5 17992.0 17486.5 16188.5 15035.0 15782.0 16204.0 18856.5
[19] 12639.0 15587.0

...

Interesting question: what is the distribution of these values?

The distribution of the sample means is an example of a sampling distribution.

For the first sample, \(\bar x_1\) = 15564

For the second sample, \(\bar x_2\) = 14651.5

For the third sample, \(\bar x_3\) = 16365.5

For the forth sample, \(\bar x_4\) = 17454.5

For the fifth sample, \(\bar x_5\) = 15201

For the sixth sample, \(\bar x_6\) = 16241

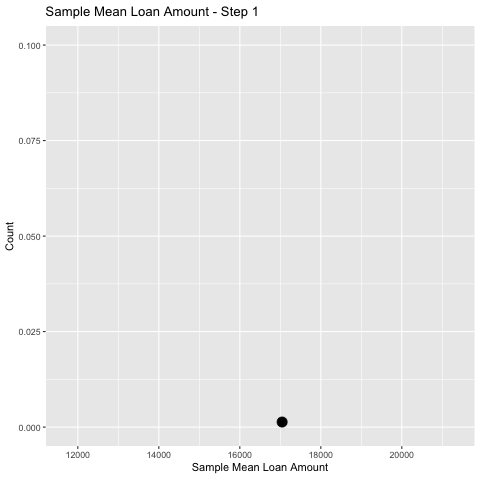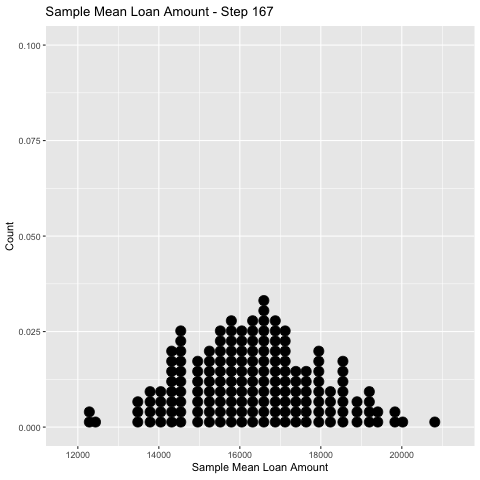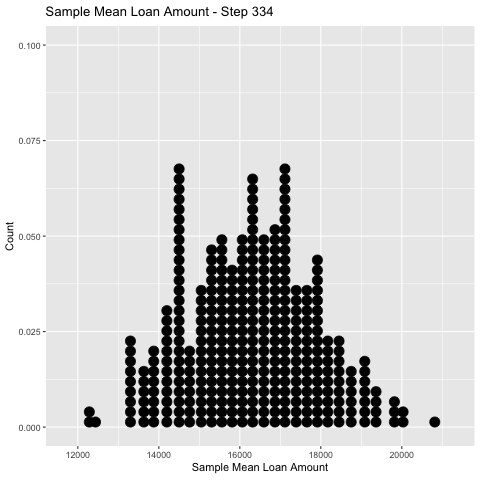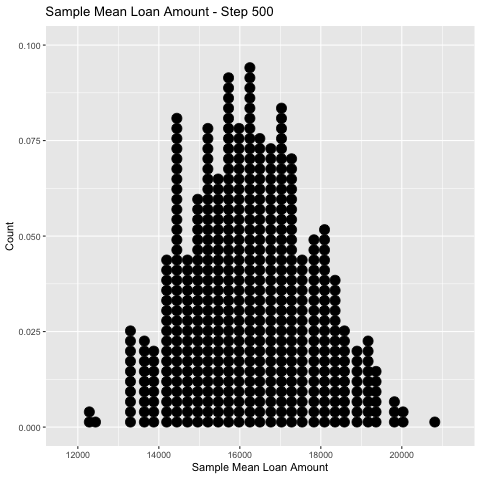
In simulation land, I can take as many random samples as I like.

👈 Here I take 500 samples of size \(n=50\) and keep track of the sample mean, \(\bar x\), for each.

⏩ The collection of \(\bar x\)’s forms an rough estimate of the probability distribution of \(\bar X\).

In simulation land, I can take as many random samples as I like.

👈 Here I take 500 samples of size \(n=50\) and keep track of the sample mean, \(\bar x\), for each.

⏩ The collection of \(\bar x\)’s forms an empirical approximation of the sampling distribution of the sample mean \(\bar X\).

this was created in

Stat205/r/sampling-distribution-dots.R

You can play with simulations at StatKey: Sampling Distribution for a Mean

Empirical Sampling Distribution

To get an empirical estimate of the distribution, we plot a histogram of sample means we have observed.

• We note that when the sample size is at least moderately large, the distribution of the sample mean is approximately normal

• This phenomenon is known as the CLT, which states that a sampling distribution of the mean will approach a normal distribution as the number of trials increases (as long as the sample size is large enough).

Theoretical Sampling Distribution

Thanks to the Central Limit Theorem we actually know what the theoretical probability distribution of \(\overline{X}\) is …

Let \(X_1, X_2, . . . , X_n\) be nindependently drawn observations from a population with mean μ and standard deviation σ. Let X̄ be the sample mean of these \(n\) independent observations. Then

• \(\mu_\overline{X} = \mu\). (The mean of the sampling distribution ofX̄is equal to the meanof the distribution from which we are sampling.)

• \(\sigma_{\overline{X}} = \sigma/\sqrt{n}\) (The standard deviation of the sampling distribution of X̄ is equal to the standard deviation of the distribution from which we are sampling, divided by the square root of the sample size.)

• If the distribution from which we are sampling is normal, the sampling distribution of X̄ is normal

• for large sample sizes the sampling distribution of the sample mean will be approximately normal, regardless of the distribution from which we are sampling.That is the gist of the central limit theorem, but let’s fill in a few details

Theoretical Sampling Distribution

Thanks to the Central Limit Theorem we actually know what the theoretical probability distribution of \(\overline{X}\) is …

Theorem 1 (Central Limit Theorem (CLT)) Under appropriate conditions ¹, the distribution of the sample mean \(\overline{X}\) is approximately normal, with mean \(\mu_{\bar x} = \mu\), the population mean and standard deviation, aka the standard error (SE), given by \(\sigma_{\overline{X}} = \frac{\sigma}{\sqrt{n}}\). We often write:

\[ \overline{X} \;\approx\; N\!\left(\mu,\; \frac{\sigma}{\sqrt{n}}\right). \]

the distribution of sample means (averages) from any large sample size, drawn from almost any population, will be approximately a normal (bell-shaped) distribution, even if the original population isn’t normal.

provided the observations are independent and identically distributed and the population has a finite mean and variance.

It says the probability distribution of \(\overline{X}\) approaches a Normal distribution as long as the sample size is large enough.

1. sufficiently large sample sizes (rule of thumb is \(n \geq 30\)), observations are independent and identically distributed (i.i.d), the population has a finite mean and variance.

CTL Visualized

iClicker

Understanding Sampling Distributions

A sampling distribution represents:

1. The distribution of a sample.

2. The distribution of a population.

3. The distribution of a statistic, like the sample mean, across repeated samples.

4. The distribution of a parameter, like the population mean.

iClicker

Central Limit Theorem

According to the Central Limit Theorem, the sampling distribution of the sample mean:

1. Always follows a normal distribution regardless of sample size.

2. Becomes approximately normal as the sample size increases.

3. Becomes approximately normal as the number of samples increase.

4. Has a standard deviation equal to the population standard deviation.

5. Is skewed when the population distribution is skewed.

iClicker

Variability of the Sample Mean

As the sample size increases, the variability of the sample mean:

1. Increases.

2. Decreases.

3. Remains constant.

4. Depends on the population distribution.

Sampling Distribution

Definition: Sampling Distribution

A sampling distribution is the probability distribution of a statistic

In other words, if were were to repeatedly draw samples from the population and compute the value of the statistic (e.g. sample mean, or variance), the sampling distribution is the probability distribution of the values that the statistic takes on.

Important

In many contexts, only one sample is observed, but the sampling distribution can be found theoretically.

• If an arbitrarily large number of samples, each involving multiple observations (data points), were separately used in order to compute one value of a statistic (such as, for example, the sample mean or sample variance) for each sample, then the sampling distribution is the probability distribution of the values that the statistic takes on.

• Sampling distributions are important in statistics because they provide a major simplification en route to statistical inference. More specifically, they allow analytical considerations to be based on the probability distribution of a statistic, rather than on the joint probability distribution of all the individual sample values.

Standardizing

• Recall that we can standardize any normal RV, say \(X\sim\)Normal(\(\mu\), \(\sigma\)) to the standard normal distribution, i.e. a Normal(0, 1)

• The standardization formal is

  \[ Z = \dfrac{X -\mu}{\sigma} \]

  where \(Z \sim\) Normal(0,1)

• Z tells us how many standard deviations X is away from the mean.

• Standardization allows us to use the standard normal table to find probabilities.

Standardizing a Sample Mean

If we take a sample of size \(n\), the mean \(\bar{X}\) follows:

\[ \bar{X} \sim \text{Normal}\left(\mu_{\bar X} = \mu, \sigma_{\bar X} = {\sigma}/{\sqrt{n}}\right) \]

To standardize the sample mean:

\[ Z = \frac{\bar{X} - \mu_{\bar X}}{\sigma_{\bar X}} = \frac{\bar{X} - \mu}{\sigma / \sqrt{n}} \sim \text{Normal}(0,1) \]

Starting from the Central Limit Theorem, we can see how the familiar standard normal distribution arises.

This accounts for sampling variability. Used in hypothesis testing and confidence intervals.

• The Central Limit Theorem (CLT) is a fundamental concept in statistics that describes the behavior of the sampling distribution of the sample mean as the sample size increases, regardless of the original distribution of the population.
• The numerator shrinks to 0 as \(n \to \infty\) because \(\bar{X}\) is converging to \(\mu\)
• The denominator also shrinks, since \(\frac{\sigma}{\sqrt{n}}\)​ decreases as \(n\) grows.

Key Idea:

• If we just looked at \(\bar{X}\) it would converge to \(\mu\) with a vanishing standard deviation.

• But when we standardize using \(Z_n\)​, the random fluctuations remain on the same scale for all \(n\), which is why the limiting distribution is standard normal.

However, the rate of shrinking is exactly balanced in such a way that their ratio remains a random variable with constant variance.

🔑 Many inferential procedures (such as calculating probabilities, confidence intervals, and test statistics) rely on this standardized version of the sampling distribution.

Empirical Rule

The Empirical Rule, or 68-95-99.7 rule, describes data distribution in a normal (bell-shaped) curve:

• approximately 68% of data falls within one standard deviation of the mean,
• 95% within two standard deviations
• 99.7% within three standard deviations

providing a quick way to understand data spread and identify potential outliers.

Why Standardize?

We standardize so that different problems can be compared using the same reference distribution.

Exam scores

Example 1 Suppose we are interested in exam scores from two different courses:

• Course A: mean = 65, standard deviation = 5
• Course B: mean = 80, standard deviation = 10

A student scores 75 in both courses.

Without standardization: A score of 75 looks “the same” in both courses.

Solution

After standardizing:

• \(z_A = \frac{75 - 65}{5} = 2\)
• \(z_B = \frac{75 - 80}{10} = -0.5\)

Interpretation:

• In Course A, the student is far above average
• In Course B, the student is below average

There are two ways we’ll be answering inferential questions:

1. Z-tables (click here to download)
   • Used to look up probabilities and Z-scores
   • Commonly used when working by hand (e.g. hand-written assignment questions, midterms, final)
2. R
   • Computes probabilities, quantiles, test statistics, confidence intervals directly
   • Useful for checking work and what you will commonly use in practice.

Course Expectation

Important

You should be able to answer inference questions by hand and in R.

✍️ Pros for by-hand ✍️

• 🧠 Build understanding

• 🔍Develops Critical Thinking

• 📝 Essential for exams

💻 Pros for R 💻

• ⚡ Fast and accurate calculations

• 📊 Handles complex computations easily

• 🛠️ Standard tool in practice

Finding Probabilities Using Z-scores

To find \(\Pr(X < 180)\) we use the standard normal distribution formula:

\(\Pr(X < 180) =\) \(\Pr\left(\dfrac{X -\mu}{\sigma} < \dfrac{180 -\mu}{\sigma}\right)\)

\(\phantom{\Pr(X < 180)}=\Pr\left(Z < \dfrac{180 -170}{8}\right)\)

\(\phantom{\Pr(X < 180)}=\Pr\left(Z < \dfrac{10}{8}\right)\)

\(\phantom{\Pr(X < 180)}=\Pr\left(Z < 1.25\right)\)

\(\phantom{\Pr(X < 180)}=\quad ?\)

At this point we can consult our Z-table

To find \(\Pr(X < 180)\) we can equivalently find \[ \Pr(X < 180) = \Pr\left(\frac{X - \mu}{\sigma} < \frac{180 -\mu}{\sigma}\right) = \Pr\left(Z < \frac{180 -170}{8}\right) \]

Use this table to find probabilities for
positive Z-scores!

Use this table to find
probabilities for
negative Z-scores!

Probabilities in R

Note

Notice how \(Z \sim N(0,1)\) is the default

pnorm(q, mean = 0, sd = 1, lower.tail = TRUE)

q

vector of quantiles

mean

mean (default is 0)

sd

standard deviation (default is 1)

lower.tail

logical; if TRUE (default), probabilities are \(\Pr(X \leq q)\) otherwise \(\Pr(X > q)\)

pnorm for Standard Normal

For the standard normal we use the defaults

\(\Pr(Z < q)\)

pnorm(q)

\(\Pr(Z \geq q)\)

pnorm(q, lower.tail = FALSE)

General pnorm

For some \(X \sim N(\mu = \texttt{mu}, \sigma = \texttt{sig})\)…

\(\Pr(X < q)\)

pnorm(q, mean=mu, sd=sig)

\(\Pr(X \geq q)\)

pnorm(q, mean=mu, sd=sig, lower.tail = FALSE)

Visualize Probabilities

\(\Pr(X < 180)\) where \(X \sim N(170, 8)\)

pnorm(180, mean = 170, sd = 8)

[1] 0.8943502

\(\Pr(Z < 1.25)\) where \(Z \sim N(0, 1)\)

pnorm(1.25)

[1] 0.8943502

Finding Probabilities Using Z-scores

To find probabilites for \(X\sim N(\mu, \sigma)\)

1. Convert \(X\) to a \(Z\)-score:

   \[ Z = \frac{x - \mu}{\sigma} = z \]

2. Use the standard normal Z-table or R

   \(P(Z < z)\)	pnorm(z)
   \(P(Z > z)\)	pnorm(z, lower.tail = FALSE)
   \(P(a < Z < b)\)	pnorm(b) - pnorm(a)

Examples

Household Groceries (iClicker)

Exercise 1 Weekly Grocery Expenses The weekly grocery expenses for households in a certain region follow the the distribution given in Figure 1. According to a national consumer survey, the average grocery expense for this region is 107 with a standard deviation of \(38\). A random sample of 30 households is selected from this population.

What is the sampling distribution¹ of \(\bar X\)?

1. \(\bar X \sim N(0,1)\)
2. \(\bar X \sim N(107,38)\)
3. \(\bar X \sim N(107,38/30)\)
4. \(\bar X \sim N(107,38/\sqrt{30})\)
5. None of the above

Figure 1: Distribution of weekly grocery expesnse for housholds in a certain region.

1. We are using the \(N(\mu, \sigma)\) parameterization

✏️ Household Groceries

Exercise 2 Weekly Grocery Expenses The weekly grocery expenses for households in a certain region follow the the distribution given in Figure 1. According to a national consumer survey, the average grocery expense for this region is 107 with a standard deviation of \(38\). A random sample of 30 households is selected from this population.

Distribution of weekly grocery expesnse for housholds in a certain region.

What is the probability that the average weekly grocery expense for a randomly selected sample of 30 households exceeds $120?

Solution

Summary

🔹 Although the population distribution is skewed, the CLT tells us that the sampling distribution of \(\bar{X}\) can be approximated by a normal distribution when the sample size is sufficiently large.

🔹 We standardize \(\bar X\) to find probabilities on the standard normal curve.

Note that this distribution is right-skewed.

Using simulation, check whether this holds for a sample size of 40.

1. Compute the mean and standard deviation of the sample mean.

2. Describe the shape of the sampling distribution.

3. If we simulated 1000 samples of 40 households and plotted the sample means, what would you expect the histogram to look like?

Rolling a die

Rolling a die

Example 2 What is the sampling distribution of the average number of dots facing up 5 dice?

We first need to identify the distribution of \(X_i\)

We’ll solve this first theoretically using the CLT and then empirically using simulation.

Mean and standard error

\(\mathbb{E}(X_i)\)

• \(\mathbb{E}(X_i) = \frac{a + b}{2} = \frac{1 + 6}{2} =\) 3.5 and
• \(\text{Var}(X_i) = \frac{(b-a+1)^2-1}{12} = \frac{(6 - 1 + 1)^2 - 1}{12}\) 2.9166667

Theoretical Result

Population Distribution: \(X_i \sim Unif(1,6)\) with mean and var cal on previous page

Let \(X_i\) be the number of dots facing up when rolling a fair die.

When we roll the die 5 times and calculate the sample mean, the sampling distribution of the mean has the following properties:

• The mean of the sampling distribution (\(\mu_{\bar{x}}\)) is equal to the population mean

• The standard error of the mean (\(\text{SE}\)) is equal to the population sd/ sqrt(n)

Let \(\overline{X} = \frac{X_1 + X_2 + \dots X_5}{5}\) be the mean of five rolls.

Then from the CLT we know: \[ \begin{align*} \overline{X} &\sim N(\mu_{\overline{X}} = 3.5, \sigma_{\overline{X}} = \frac{\sqrt{((6-1+1)^2 -1)/12)}}{\sqrt{5}})\\ &\sim N(\mu_{\overline{X}} = 3.5, \sigma_{\overline{X}} = 0.7637626) \end{align*} \]

The mean of the sampling distribution (\(\mu_{\bar{x}}\)) is equal to the population mean: \[ \mu_{\bar{x}} = \mu = 3.5 \]

The standard error of the mean (\(\text{SE}\)) is: \[ \text{SE} = \frac{\sigma}{\sqrt{n}} = \frac{\sqrt{\frac{35}{12}}}{\sqrt{5}} \approx 0.764 \]

Empirical Result

The sampling distribution of the mean of 5 rolls of a fair die:

• Mean: \(3.5\) and Standard Error: \(\approx 0.764\)
• Approximate normal, but slightly influenced by the uniformity of the die’s outcomes.

The shape of the sampling distribution depends on \(n\): demo Baseball players https://www.lock5stat.com/StatKey/sampling_1_quant/sampling_1_quant.html

• For small \(n\), the distribution may not look perfectly normal and instead resemble the uniform distribution of a single roll.
• However, with \(n = 5\), the Central Limit Theorem suggests that the distribution will approximate a normal distribution, though not perfectly, due to the small sample size.

n = 1

with a sample size of one we just get back the original distribution

The sample mean directly reflects the shape of the population distribution.

n = 10

n = 30

Same shape but what about the x-axis?

Difference Sample Sizes

• smaller sample sizes lead to sampling distributions with a higher variance (or standard error)
• a bigger sample tends to provide a more precise point estimate than a smaller sample.
• sample means become more and more reliable as an estimate of μ as the sample size is increased, as we would expect.

Comments

• The sampling distribution gets “pointier” as the sample size increases

• Hence as \(n\) increases the SE decreases

  • Interpretation: sample means are more spread out and less accurate

• Hence as \(n\) decrease the SE increases

  • Interpretation: sample means are tightly clustered and more accurate

SE tells us how accurate the mean of any given sample is likely to be as an estimate of the actual population mean.

SE large, the sample means in the SDSM are more spread out, so it’s less likely that any given sample mean is an accurate representation of the true population mean.

SE small: But when the standard error is smaller, the sample means are less spread out, so it’s more likely that any given sample mean is an accurate representation of the true population mean.

Assumptions of the CLT

1️⃣ Independence

Each observation provides new information and does not influence the others.

Common violations:

• Time series data (e.g. daily temperatures, stock prices)
• Clustered or grouped data (e.g. students within the same classroom)
• Sampling without proper randomization

Dependence typically makes the CLT approximation unreliable.

2️⃣ Identically Distributed

All observations come from the same population with the same distribution.

Common violations:

• Mixing data from different subpopulations (e.g. combining test scores from two different exams)
• Changes over time (e.g. before/after an intervention)
• Non-random sampling mechanisms

3️⃣ Finite Mean and Variance

The population has a well-defined average and spread.

When this fails:

• Extremely heavy-tailed distributions (e.g. some theoretical power-law distributions)
• Situations with infinite variance

Most real-world data used in intro statistics does satisfy this condition.

4️⃣ Large Sample Size

The CLT is an approximation that improves as \(n\) increases.

Rule of thumb:

• \(n \ge 30\) is often sufficient
• Larger \(n\) needed for skewed or heavy-tailed populations

Important

The more non-normal the population, the larger the sample size needed.

Special case: If the population distribution is normal, then the sampling distribution of \(\bar X\) is normal for any sample size \(n\).