
Data 311: Machine Learning
Lecture 10: Classification and Regression Trees
University of British Columbia Okanagan
Introduction
We have some of the basics for building/assessing models
Much of the remainder of the course we will be introducing some new models; today’s topic is tree-based methods.
Tree-based methods are simple and useful for interpretation; however, they are typically are not competitive with the some of the alternative approaches we’ll be discussing
CART
Classification and Regression Trees (AKA CART or decision trees) involve partitioning (AKA stratifying or segmenting) the predictor/feature space by simple binary splitting rules.
Since the set of splitting rules used to segment the predictor space can be summarized in a tree, these types of approaches are known as decision tree methods.
We make a prediction for an obs. using the mean/mode response value for that “region” to which it belongs.
Motivating Classification Example
Task: partition the feature space into subsets, with each subset/region corresponding to a specific class.

True classes are colour/shape-coded
Rules: Regions can only be split horizontal or vertically.
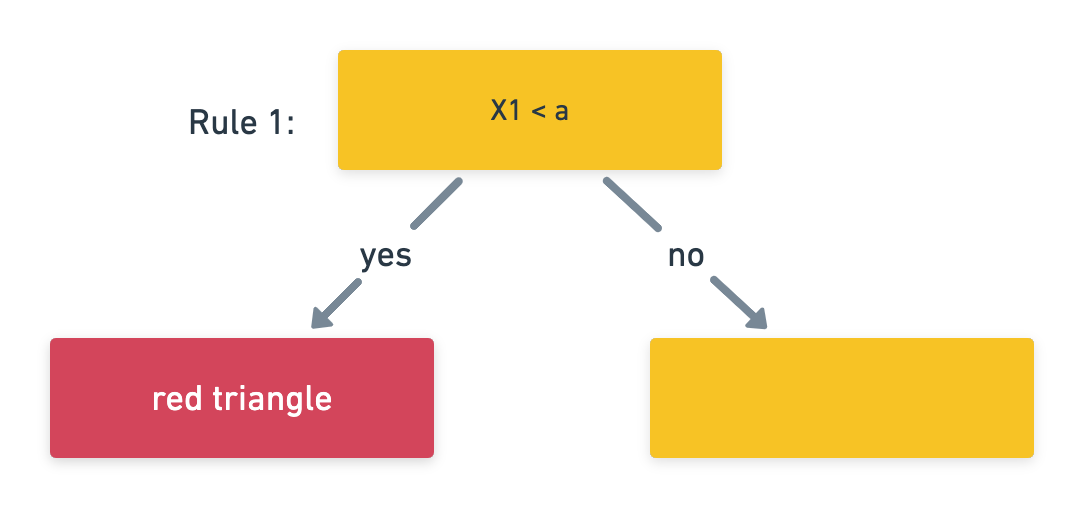
First Rule on X1
As a first go, let this line represent a decision

Rule 1:
Let’s summarize this as a flow chart:
Second Rule on X1

the left-most region is said to be pure (i.e. only containing observations from the red triangle group; see Gini Index)
Rule 2

Third Rule on X2

Rule 3

The prediction at a terminal node is the majority class for that corresponding region in the feature space.
Tree Notation
To aid with notation, try to visualize this flow chart as an upside-down binary tree with a set of connecting nodes:
The root node represents the entire population or sample and sits base of the tree.
A nodes that splits is called an internal node or decision node and is said to be the parent to its left/right child.
A node that does not split is a terminal node, or leaf.
A sub-section of an entire tree is called branch.
Notation (on tree)
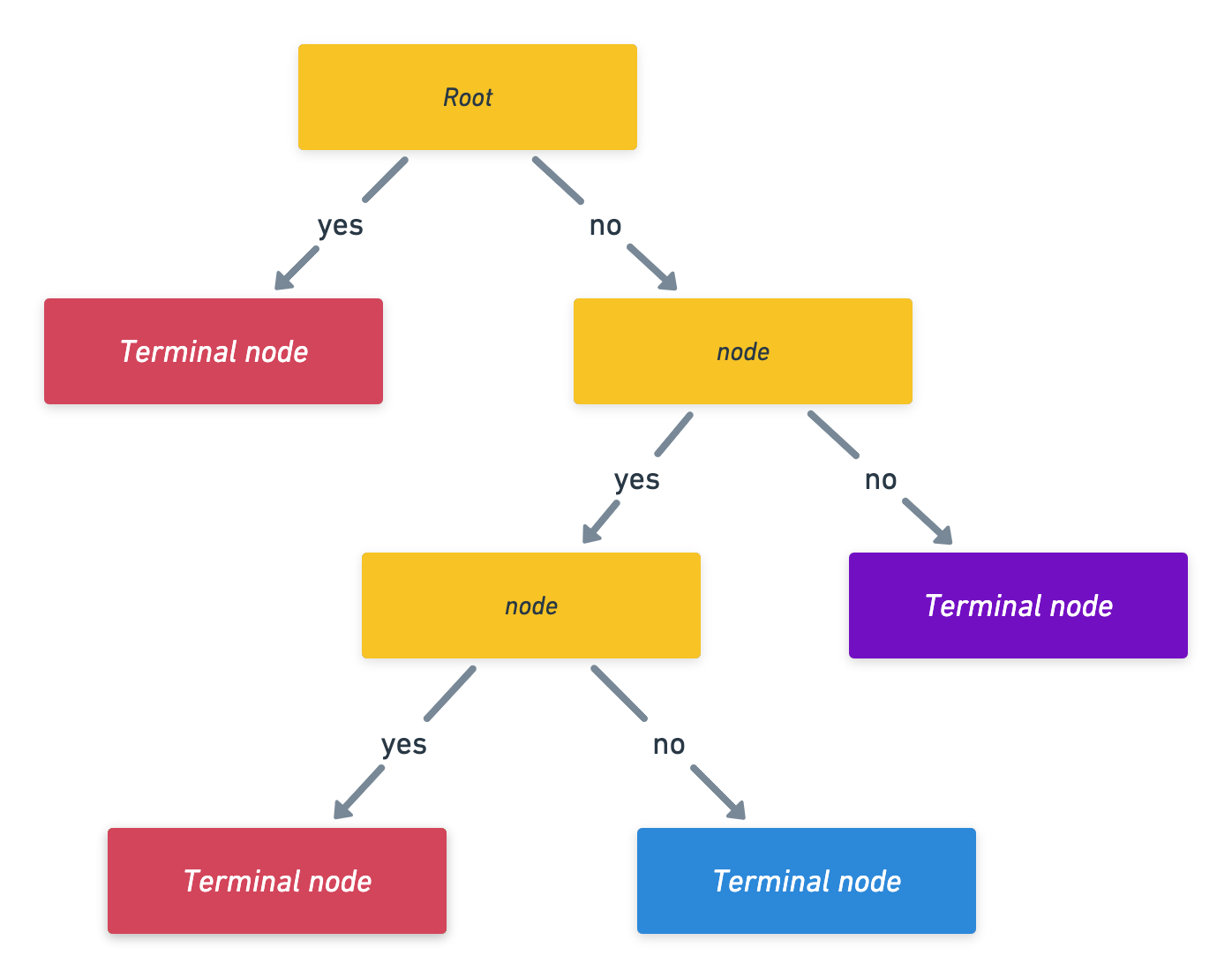
Upside-down tree
7 is parent to node 6 and 8
7 is a child to node 9
There are multiple branches (i.e. sub-trees) we can highlight
When do we stop?
Back to our motivating Classification example…
We could make more binary rules such that nothing gets misclassified …
… or could we be done with our Third Rule on X2?
8 Regions

Motivating Example: Comments
So, it appears there are some things we may need to consider going forward in the classification realm.
Before diving further into specifics, let’s motivate trees for regression through an example.
Our regression tree will be built by spliting \(X\) into partitions (or branches), and iterartively splitting partitions into smaller partitions as we moves up each branch.
Motivating Regression Example

Split 1
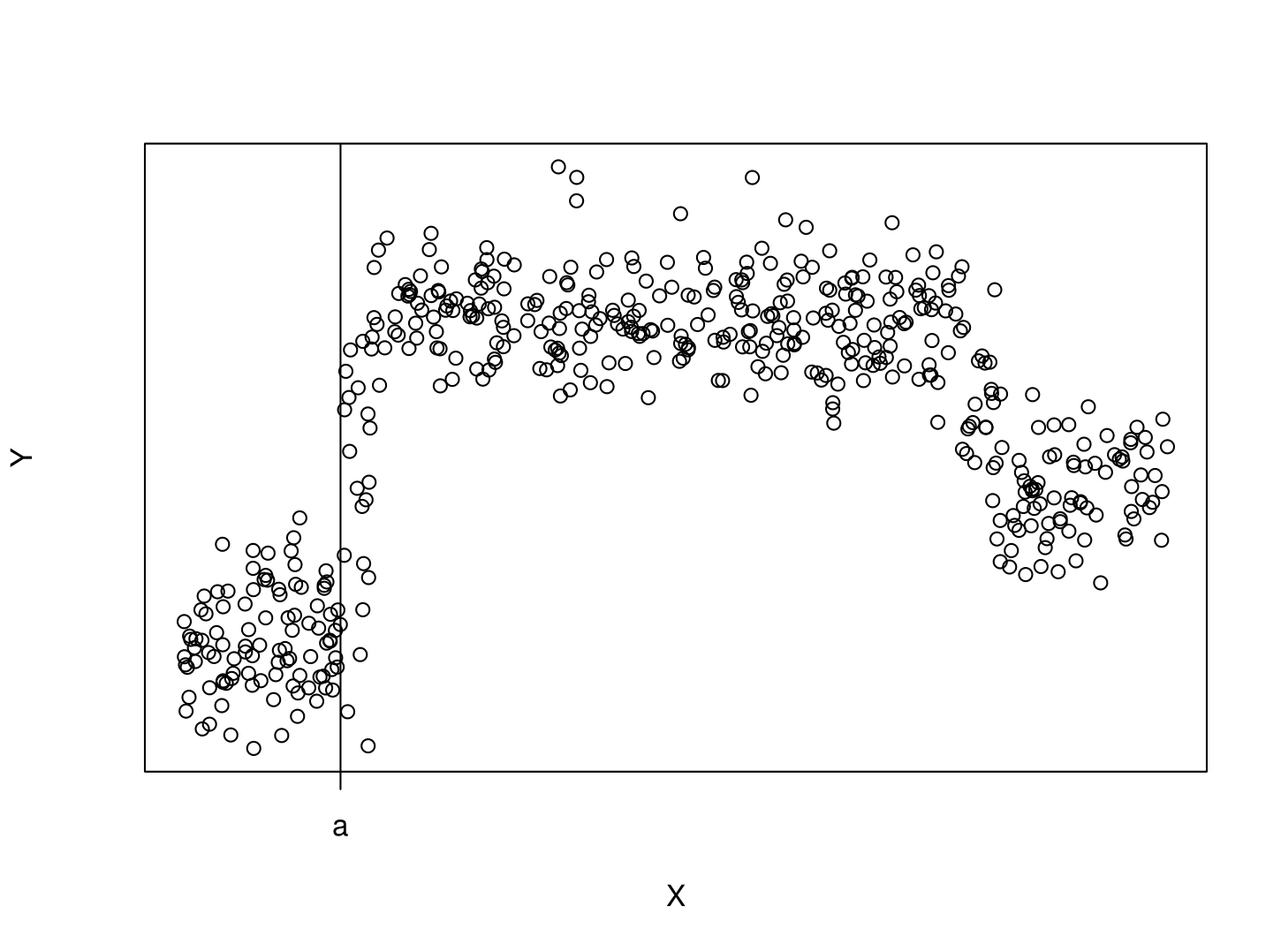
Split 2

Split 3

Split 4

Predictions?
Now that we have (five) regions of relative homogeneity in \(Y\)…what would the simplest plan be?
Easy solution is to average the observations in the region to provide the predicted value for every observation that falls into the region \(R_j\).
More generally, in order to make a prediction for a given observation, we typically use the mean or the mode response value for the training observations in the region to which it belongs.
\(Y\) Predictions

Baseball Example:


Hitters dataset from Major League Baseball player data from 1986-87. y-axis: number of years playing in the major leagues. x-axis: number of hits in the previous year. Colour: salary (low salary is blue/green, and the high salary is red/yellow)
Steps
Divide the predictor space (\(X_1\), \(X_2\), , \(X_p\)) into \(J\) non-overlapping regions1 \(R_1, R_2, \ldots, R_J\).
-
For every observation that falls into the region \(R_j\) , we make the same prediction:
Regression: Predict the mean response for the observations that fall into each region \(R_j\).
Classification: Predict the categorical response as the most commonly occurring (i.e. mode) in each region \(R_j\).
Growing a Tree
Goal
To “grow” our tree, i.e. to determine our splitting rules, we use a top-down (greedy) approach called recursive binary splitting.
It starts with all observations in a single region then splits the predictor space into two.
Then, one of those two regions are split in two (now we have three regions).
Then one of those three regions are split it two, …
Im/Possible Regions

Left: A partition of two-dimensional feature space that could not result from recursive binary splitting. Right: The output of recursive binary splitting on a two-dimensional example.
Resulting Tree


The tree (left) corresponding to the feature space partition (right).
iClicker
Terminal nodes
What is a terminal node in a decision tree?
A node that represents a decision point where further splitting is required.
A node where the tree branches into two sub-nodes.
A node used to perform cross-validation on the tree.
A node that does not split further and provides a final prediction for that region. ✅ Correct
Growing a Tree (Regression)
How do we pick a “good” split of the predictor space?
For regression the goal is to find the regions \(R_1, \dots R_J\) which minimize the RSS given by: \[RSS = \sum_{j=1}^J \sum_{i \in R_j} (y_i-\hat y_{R_j})^2\] where \(\hat y_{R_j}\) is the mean response for the training observations within the \(j\)th region; see Recursive Binary Splitting.
Determining the first split
However, we cannot consider all possible hyper-rectangles in our data-set to find the optimal tree; jump to example
Instead, we can start seek predictor \(X_j\) and cutpoint \(s\) such that the following is minimized with the resulting regions:
\[\begin{equation} \sum_{i: x_i \in R_1(j, s)} (y_i - \hat y_{R_1})^2 + \sum_{i: x_i \in R_2(j, s)} (y_i - \hat y_{R_2})^2 \end{equation}\] \[\begin{align} R_1(j, s) &= \{X\mid Xj < s\} & R_2(j, s) &= \{X\mid Xj ≥ s\} \end{align}\]
Determining the next split
Then, via the same process, we either subdivide region \(R_1\) or \(R_2\) (whichever one leads to the greatest reduction in RSS), so that we have 3 regions: \(R_1\), \(R_2\), \(R_3\)
Then we split one of these three regions further, …
The process continues until a stopping criterion is reached.
jump to example
Recursive Binary Splitting
This process of recursive binary splitting is known as a greedy approach
It’s greedy since it does not anticipate splits that will lead to a better tree in some future step, it only does the best decision at that particular step.
Consequently, this greedy approach does not ensure we find the best tree (in terms of minimum RSS) but it is computationally feasible
Stopping Criterion
We may continuing splitting until, for example:
- each region contains fewer than, say, 5 observations
- the change in the RSS is less than some \(\epsilon\)
Strategy 2 tends to produce smaller trees, but is too short-sighted. So typically we grow a larger tree than needed which we can potentially prune back.
Growing a Tree (Classification)
For classification minimizing the misclassification rate is not usually done at the growth stage as it is too “jumpy”.
Instead, usually the Gini index, deviance, or cross-entropy is used to evaluate the quality of a particular split1
Numerically these are very similar and most of the time, it won’t make a large difference which you use.
N.B. when pruning the tree (more on this in a second) we will typically use classification error rate.
Gini Index
The Gini index defined below is a measure of node inpurity1
\[G = \sum_{k=1}^K \hat p_{mk} (1-\hat p_{mk})\] where \(K\) is the number of response classes, and \(\hat p_{mk}\) is the proportion of training observations in the \(m\)th region that are from the \(k\)th class
Cross Entropy
An alternative to the Gini index is the cross-entropy, given by \[\begin{equation} D = - \sum_{k=1}^K \hat p_{mk} \log \hat p_{mk} \end{equation}\]
or the residual mean deviance (or simply deviance) given by: \[\begin{equation} -2 \sum_m \sum_k n_{mk} \log \hat p_{mk} \end{equation}\]
where \(n_{mk}\) is the number of observations in the \(m\)th terminal node that belong to the \(k\)th class.
Pruning
Problem

Building a tree through the description just given will tend to overfit1 to the training data and lead to poor test set performance.
A common strategy is to grow a large tree, \(T_0\), and then prune it back to obtain a subtree.
Intuitively, our goal is to select a subtree that leads to the lowest test error rate.
A good StatQuest video on the subject.
Cross-validation
Given a subtree, we can estimate its test error using cross-validation or the validation set approach.
However, estimating the cross-validation error for every possible subtree would be too cumbersome, since there is an extremely large number of possible subtrees.
Instead, of considering every possible subtree, we select a small set of subtrees for consideration using cost complexity pruning 1
Cost Complexity Pruning
We consider a sequence of trees indexed by a non-negative tuning parameter \(\alpha\). For every value of \(\alpha\) there corresponds a subtree, \(T \in T_0\), such that the following is minimized: \[\begin{equation} \sum_{m=1}^{|T|} \sum_{i:x_i \in R_m} (y_i - \hat y_{R_m})^2 + \alpha |T| \end{equation}\]
- Here \(|T|\) is the number of terminal nodes in the tree,
-
\(R_m\) is the region corresponding to the \(m\)th terminal node
- \(\hat y_{R_m}\) is the mean of the training observations in \(R_m\).
Tuning Parameter
When \(\alpha = 0\), then the subtree \(T\) will simply equal \(T_0\)
However, as \(\alpha\) increases, there is a price to pay for having a tree with many terminal nodes, and so the penalized RSS will tend to be minimized for a smaller subtree.
In that way, \(\alpha\) controls the trade-off between the subtree’s complexity and its fit to the training data.
It turns out that as we increase \(\alpha\) from zero, branches get pruned from the tree in a nested and predictable fashion.
Picking \(\alpha\) using CV
Using \(k\)-fold cross validation, we both build trees, and prune them back for possible values of \(\alpha\)
Each tree and subtree built in this fashion will produce an estimate of the MSE.
Pick the \(\alpha\) that minimizes the predicted MSE using the above cross-validation.
Then prune the original tree (built on the full data) with the chosen \(\alpha\).
CV Plot

Each point on this plot is calculated using these steps
Summary: Tree Algorithm
- Use recursive binary splitting to grow a large tree \(T_0\)
- Apply cost complexity pruning to the large tree in order to obtain a sequence of best subtrees, as a function of \(\alpha\).
- Use K fold cross-validation to choose \(\alpha\).
- Return the subtree from Step 2 corresponding to the chosen \(\alpha\) obtained from Step 3.
CV deviance calculations
For each \(k = 1, . . . , K\):
- Repeat Steps 1 and 2 on the \((K−1)/K\)th fraction of the training data, excluding the \(k\)th fold.
- Evaluate the mean squared prediction error1 on the data in the left-out \(k\)th fold, as a function of \(\alpha\).
- Average the results & pick \(\alpha\) to minimize the average error.
iClicker
binary splitting
Which of the following statements is true about recursive binary splitting in decision trees?
- It involves splitting nodes in a decision tree based on categorical variables only.
- It guarantees finding the global optimal tree structure.
- It uses a greedy approach to find the best split at each step. ✅ Correct
- It allows for non-binary splits to improve prediction accuracy..
iClicker
Pruning
What is the main purpose of pruning a decision tree?
To increase the size of the tree and improve its accuracy on the training data.
To reduce the complexity of the tree and prevent overfitting. ✅ Correct
To change the Gini index used in splitting criteria.
To convert a regression tree into a classification tree.
Classification Trees
For classification trees, the process is very much the same.
We use the previously mentioned Gini index for choosing splits (growing the tree), and often use the misclassification rate during the pruning stage (again with cost-complexity tuning parameter).
We predict that each observation belongs to the most commonly occurring class of training observations in the region to which it belongs.
Redo Motivating Example
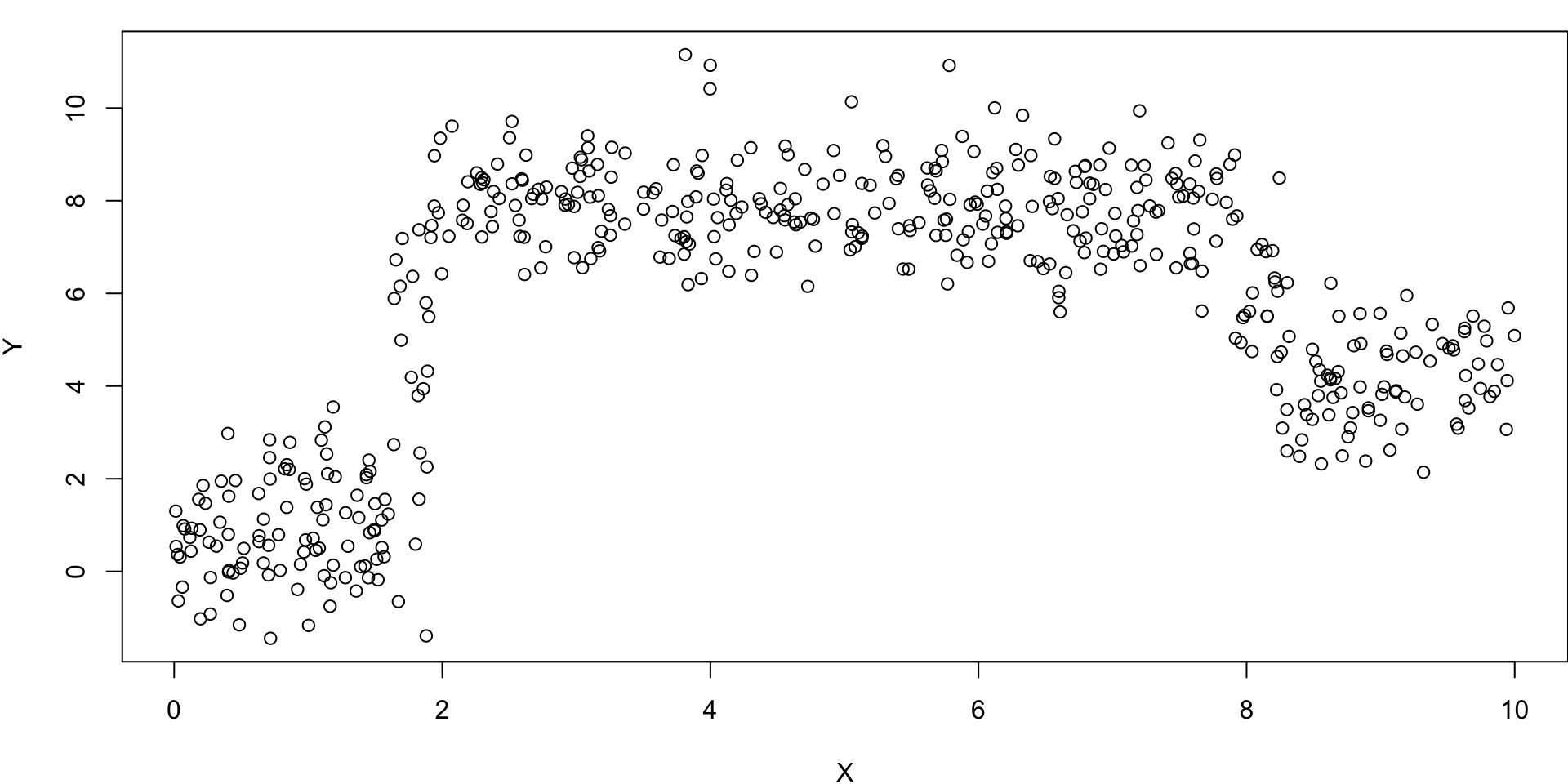

Rule 1
x < 1.88734?
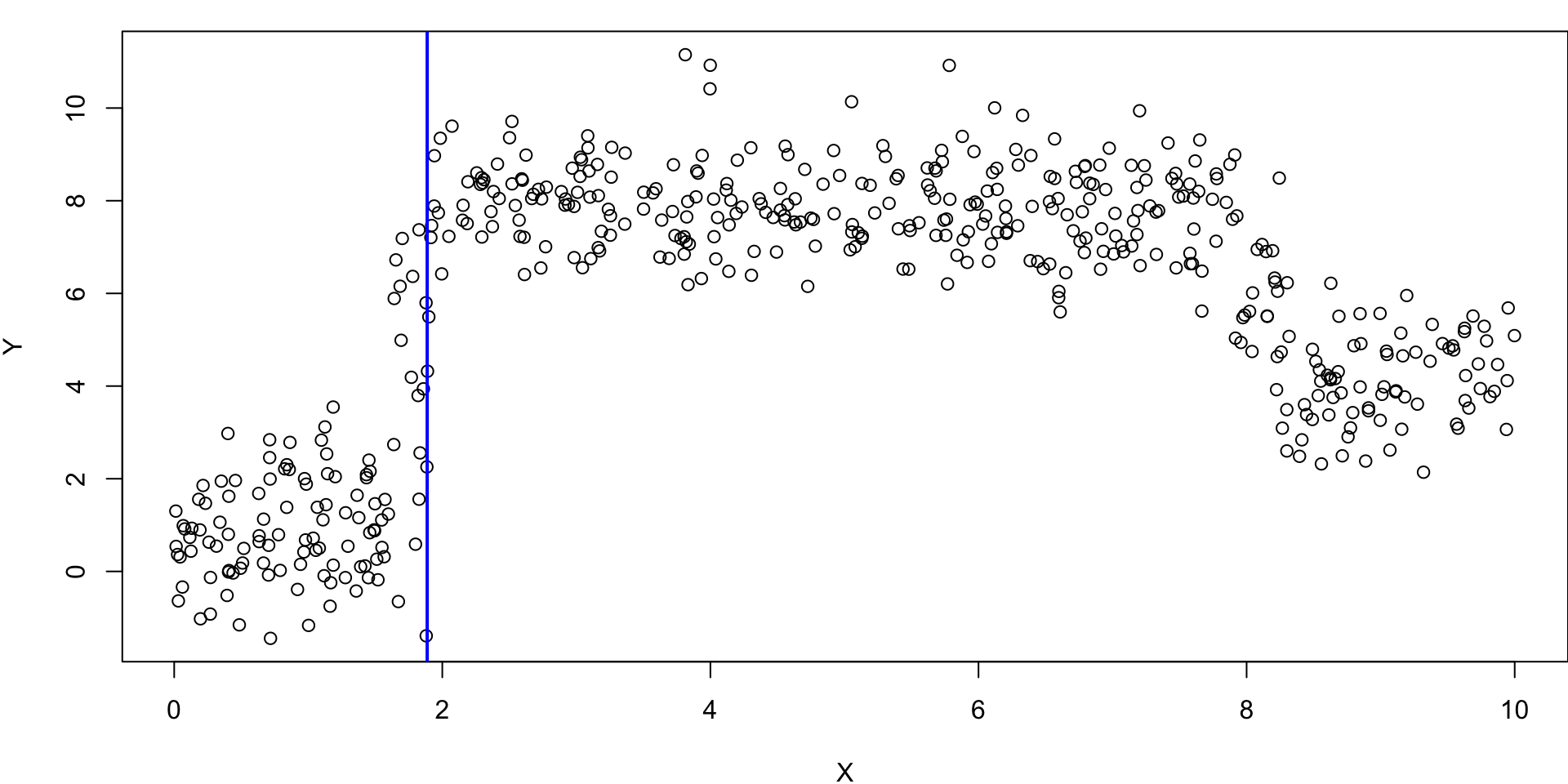

This split was determine by this
Rule 1: No. Rule 2
x < 1.61789?

This split was determined using this
Rule 1: Yes. Rule 2: Yes
predict 0.893184

Rule 1: Yes. Rule 2: No
predict 3.8922321

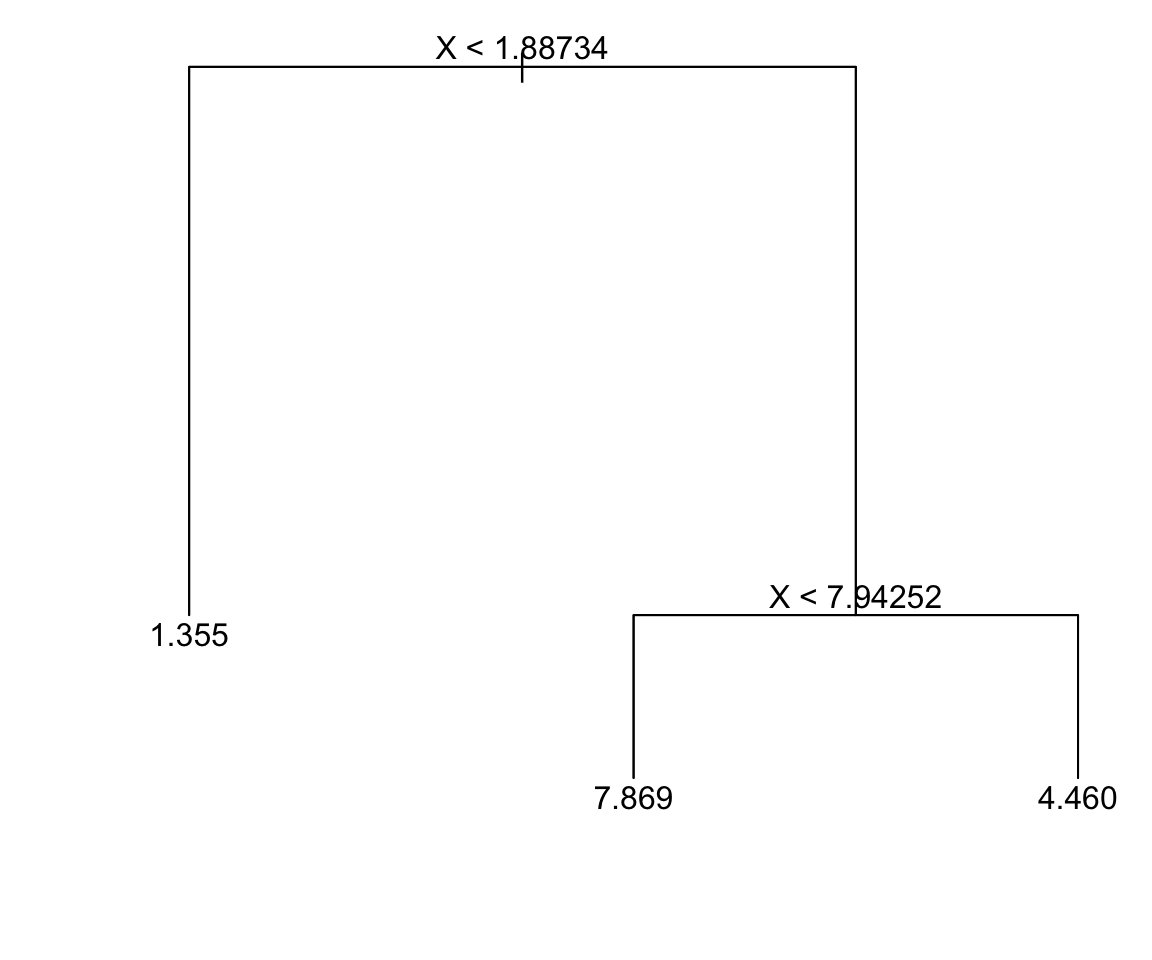
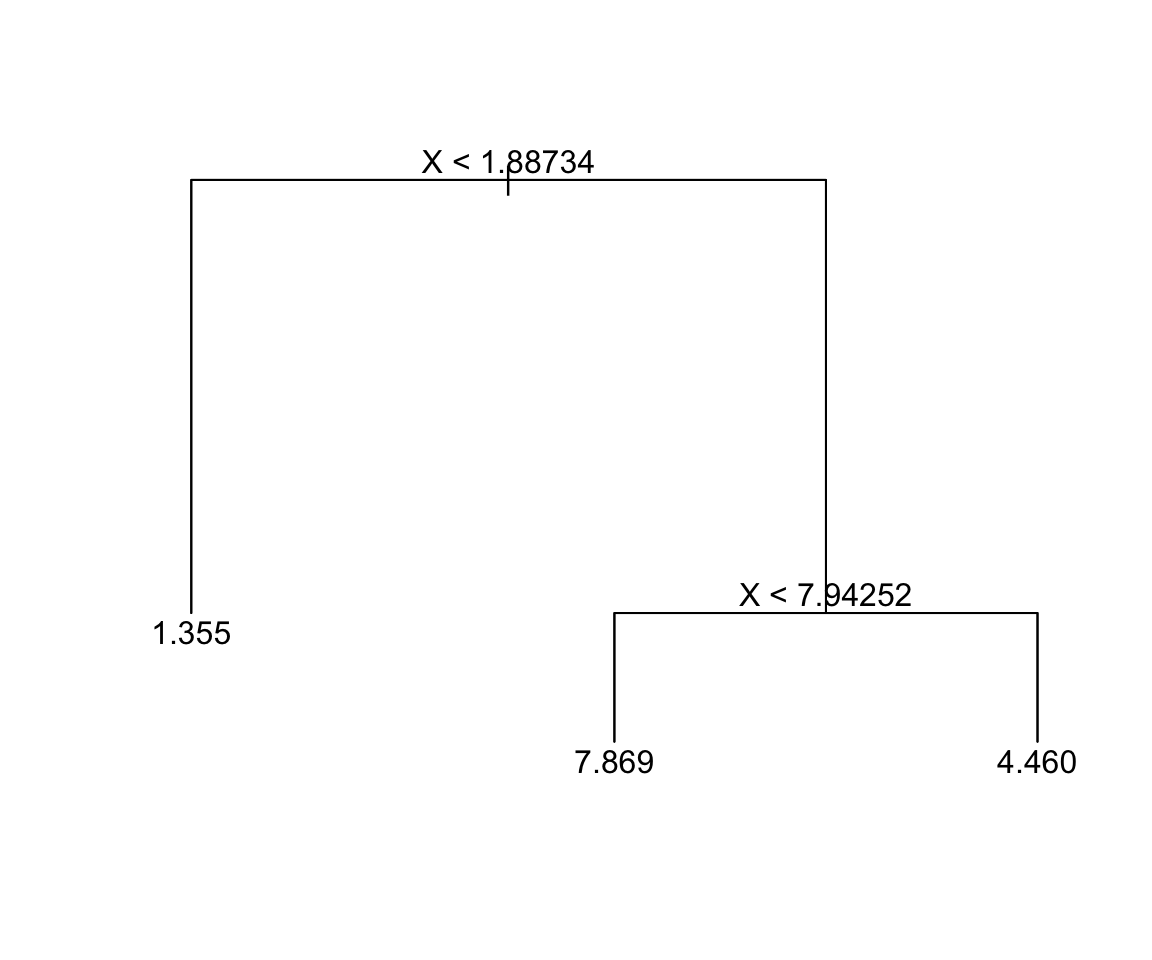
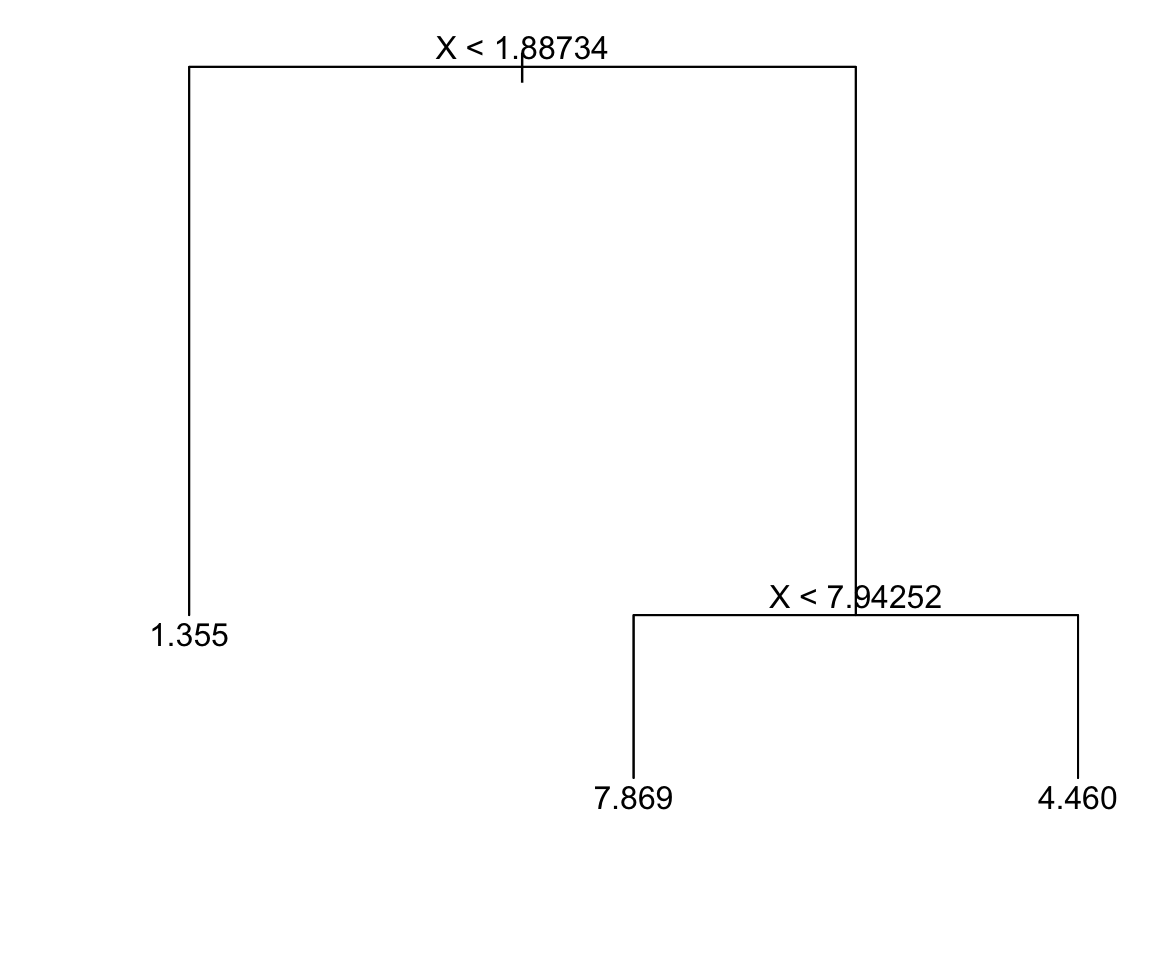
Rule 1: No. Rule 3
X < 7.94252?
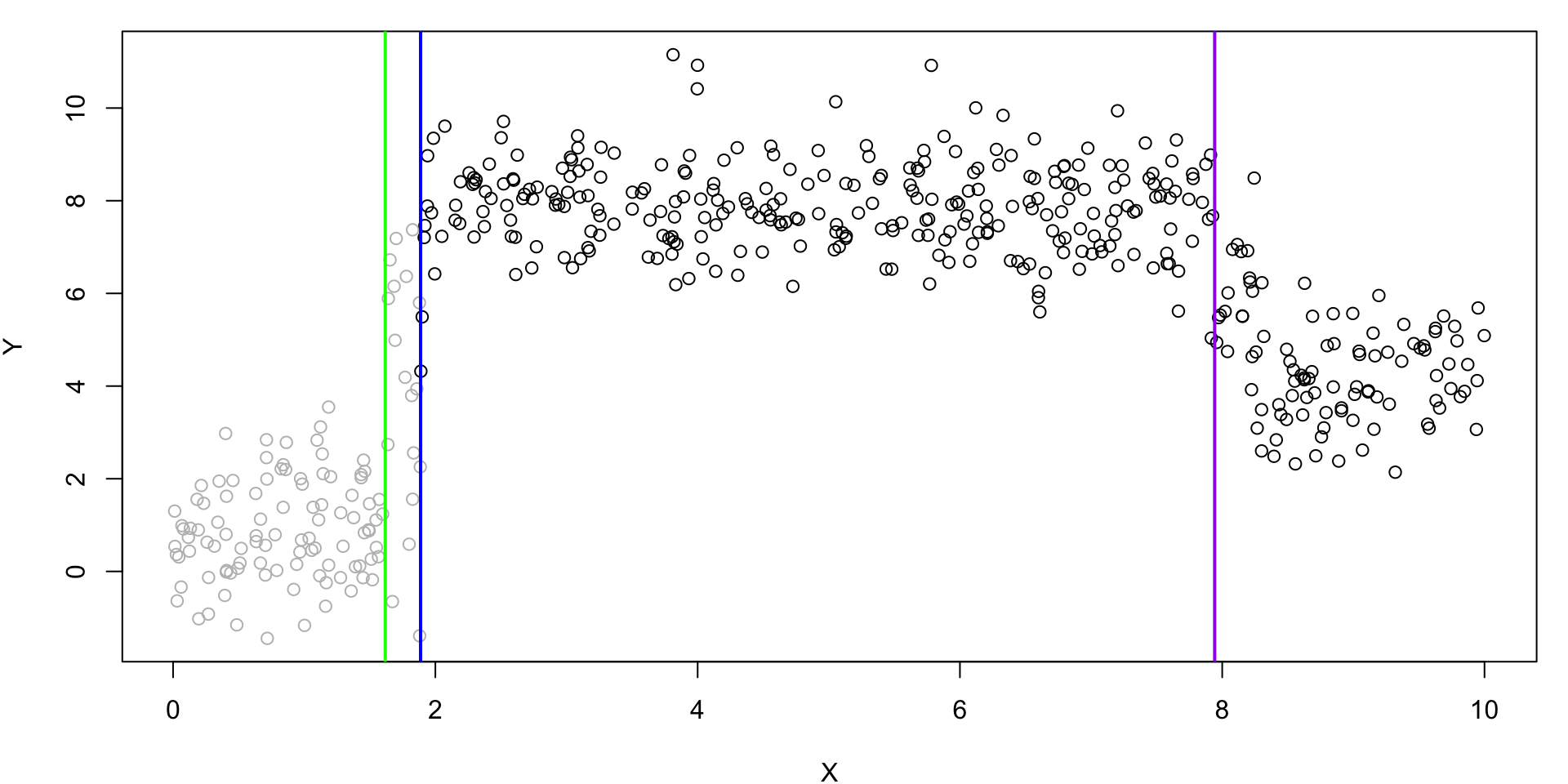

Rule 1: No. Rule 3 Yes.
predict 7.8689239


Rule 1: No. Rule 3 No. Rule 4
X < 8.25091?
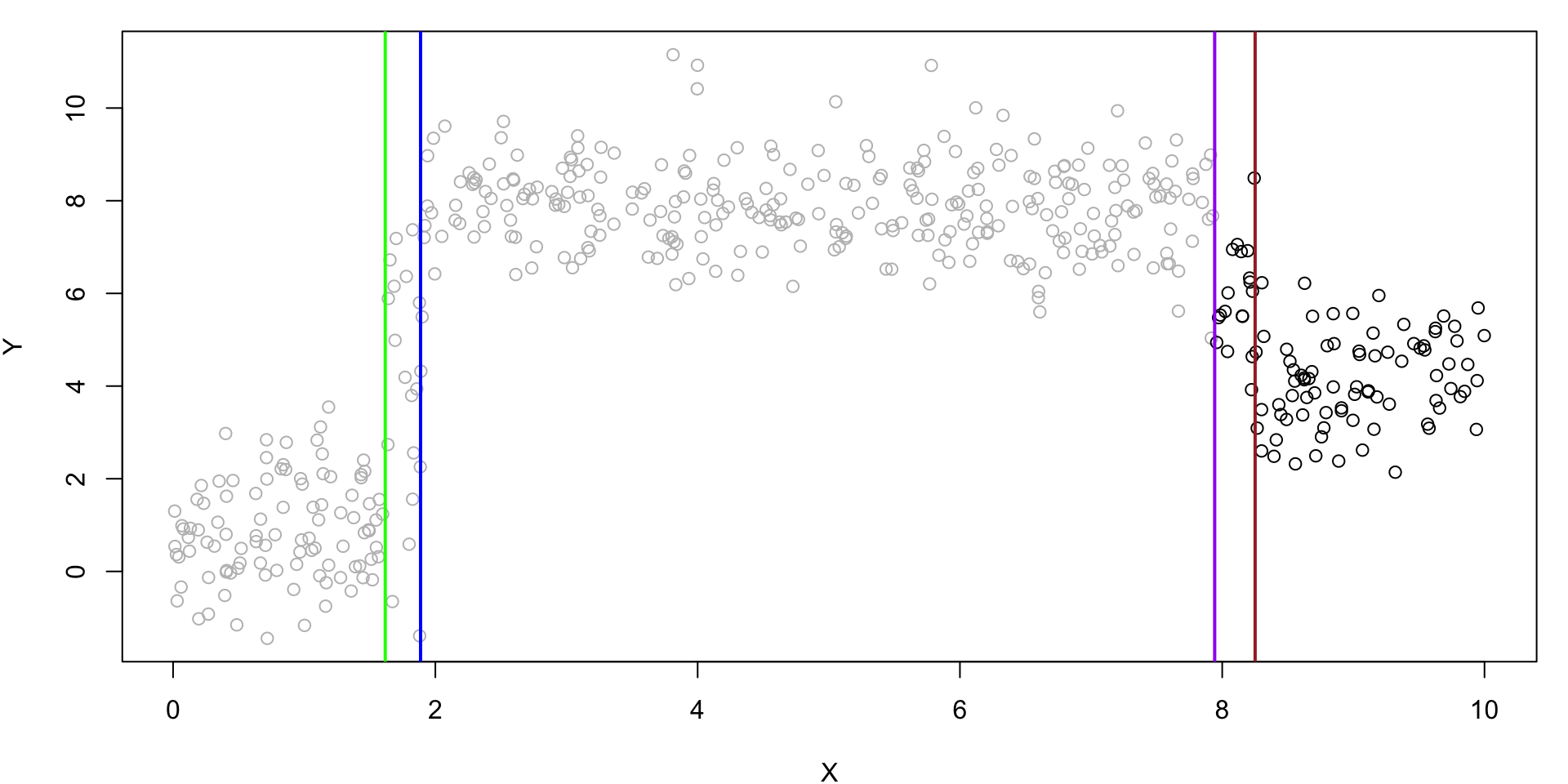

Rule 1: No. Rule 3 No. Rule 4 Yes.
predict 5.935194

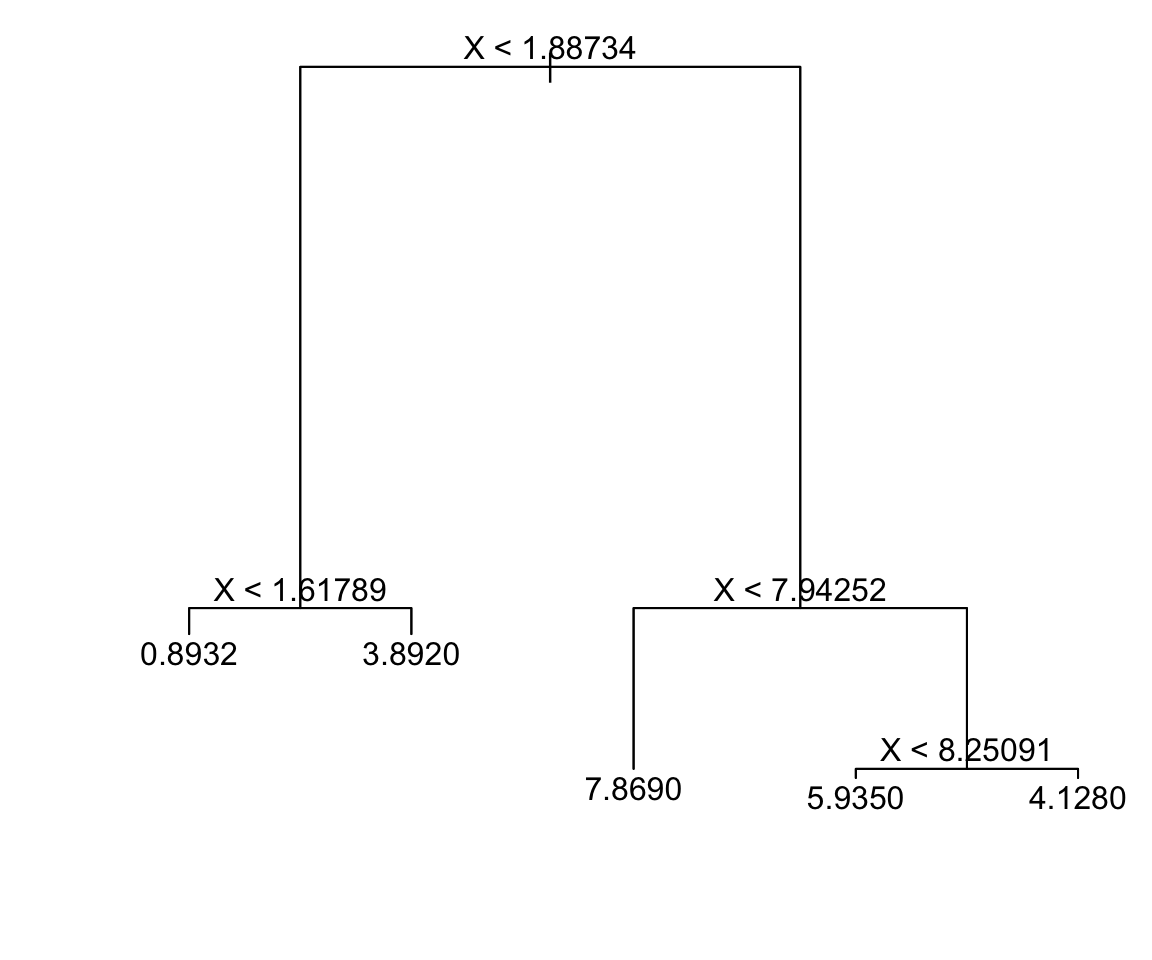
Rule 1: No. Rule 3 No. Rule 4 No.
predict 4.1281582


cv.tree
cv.tree output
-
size: no. terminal nodes as the tree was pruned back -
$devthe deviance of the pruned trees:- For regression this is the RSS
- For classification we usually change the defaults so that this corresponds to the number of cross-validation errors; see example here
-
kis the \(\log(\alpha)\)
Optimal \(\alpha\)
It turns out, no pruning needed, according to CV.

iClicker
growing a tree
When growing a regression tree, which criterion is typically used to determine the quality of a split?
- Misclassification rate.
- Gini index.
- Residual Sum of Squares (RSS). ✅ Correct
- Mean Absolute Error (MAE).
iClicker
Gini index
In a classification tree, what is the Gini index used for?
- To measure the goodness-of-fit of a regression model.
- To evaluate the impurity of a node, with lower values indicating purer nodes. ✅ Correct
- To determine the accuracy of the model’s predictions.
- To set the maximum depth of the tree.
Example: Beer
The following is a look at beer price-per-six-pack (in the 90’s) along with some consumer reports information on that beer…
-
namename of the beer -
qltyquality (scale 1-100) according to a blind taste -
calcalories -
alcalcoholic level -
bitterbitter (scale 1-100) -
maltymalty (scale 1-100)
You can find this data set here
Bushy Tree

cross validation

Pruned Tree

Non-deterministic

Pruned tree with 6 terminal nodes

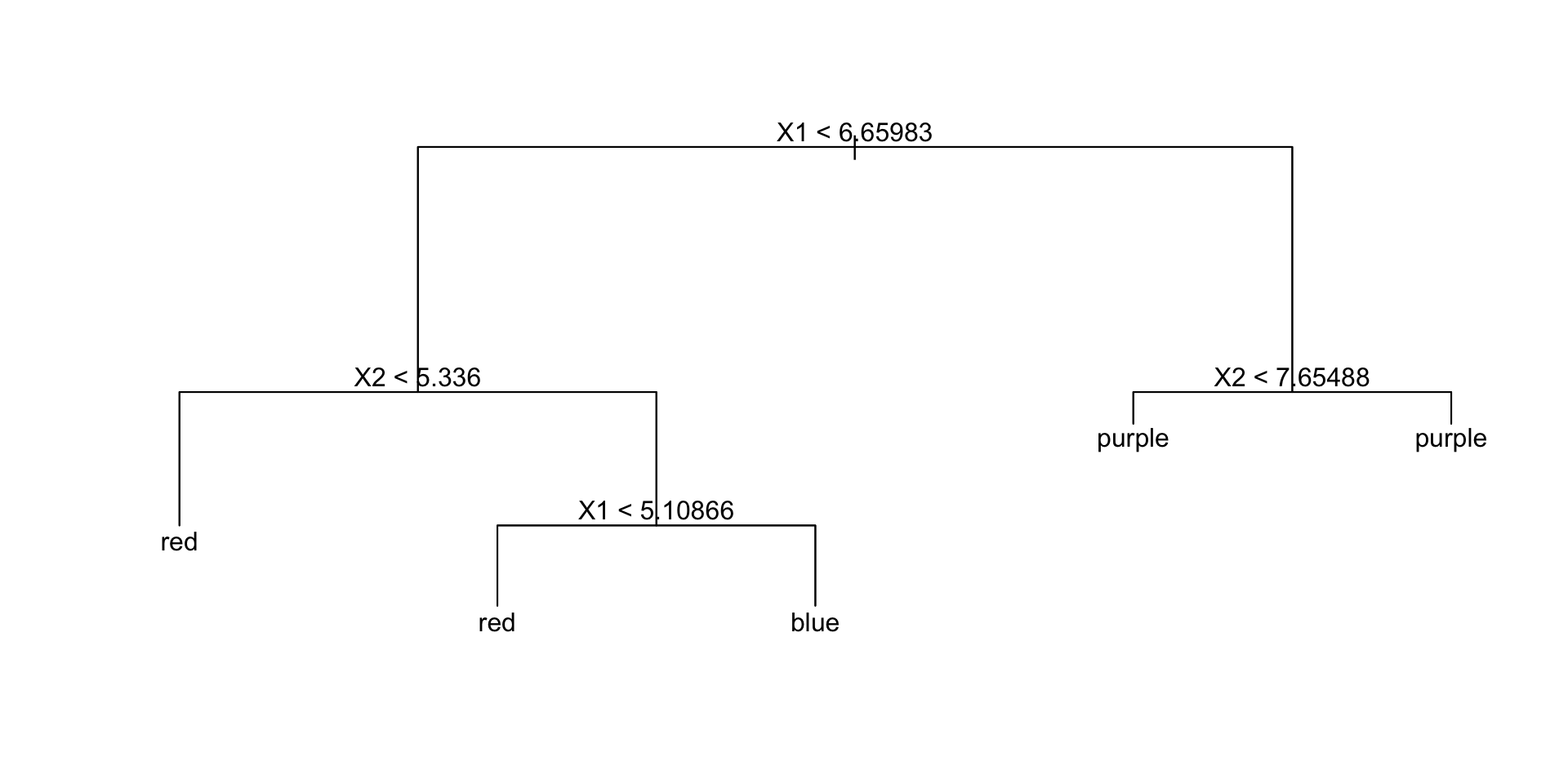
Classification Example
Back to the motivating example for classification.

Full tree
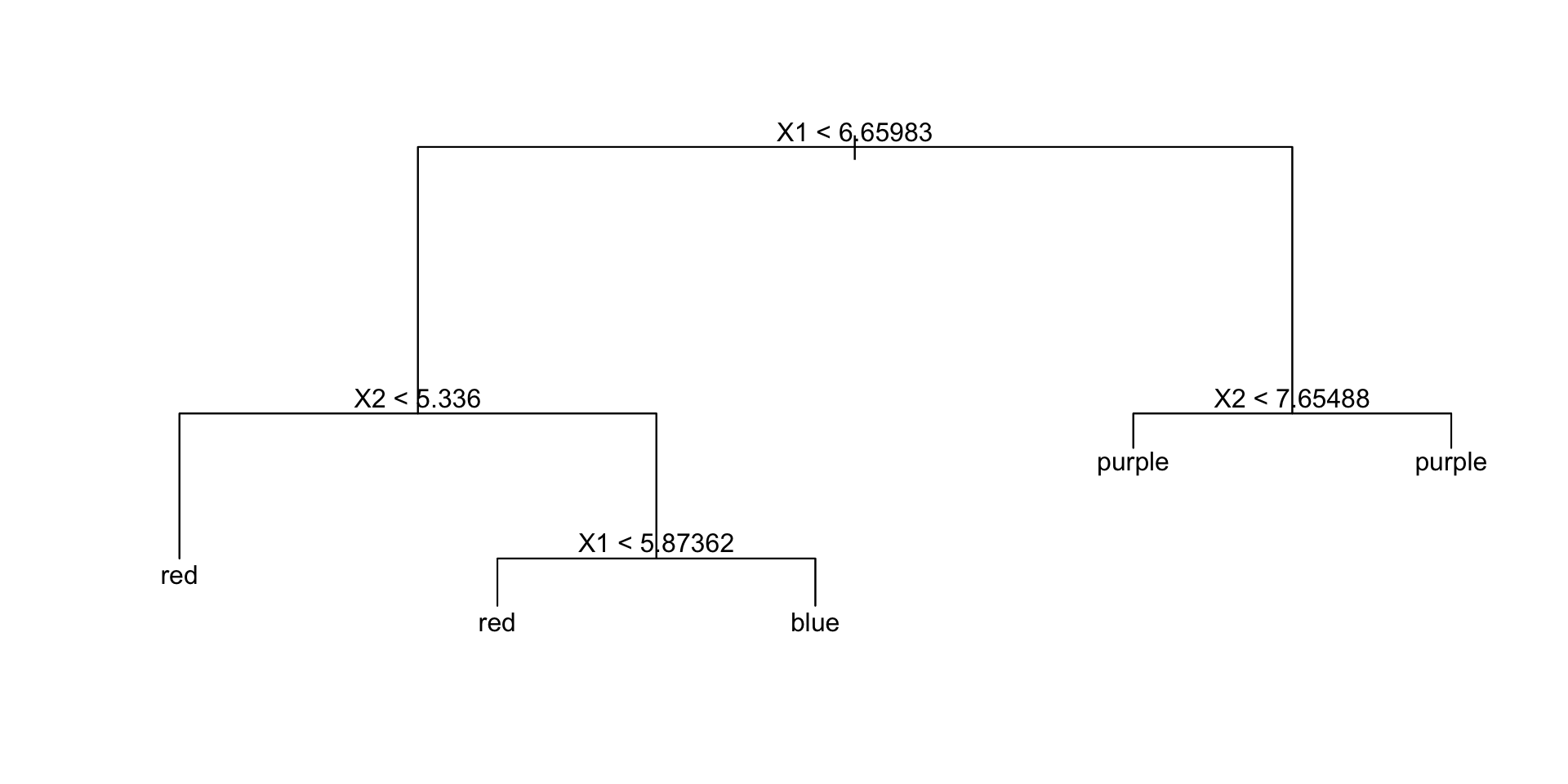
Rules
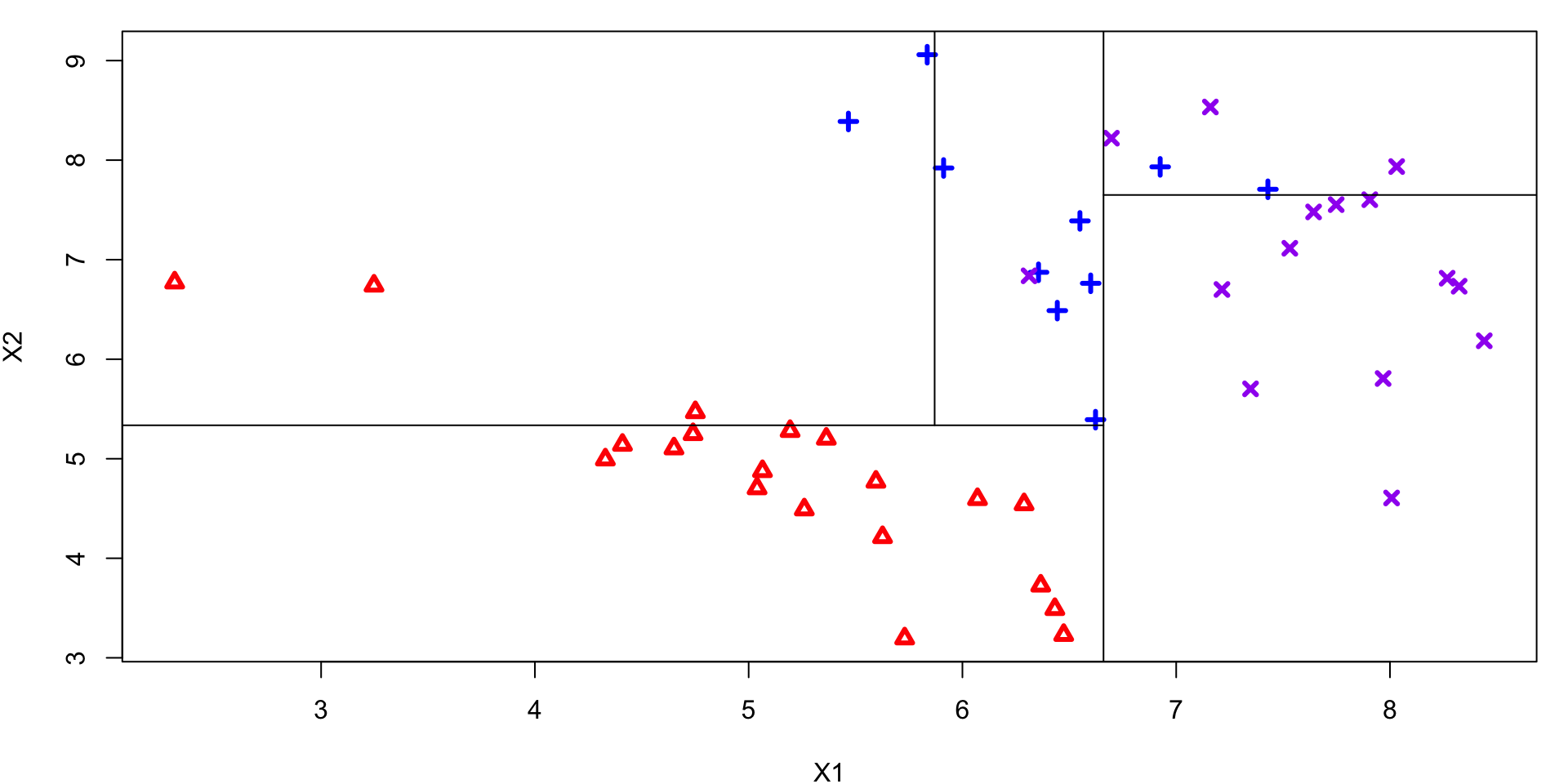
Plotted Tree
Updated Rules
Using mincut = 3 our partition of the predictor space becomes …

No further pruning needed
Change the error metric from deviance to misclassification:

Motivating Example: Classification
Predicted
True blue purple red
blue 8 2 0
purple 1 14 0
red 0 0 20Misclassification rate: 3/45 = 0.0666667. Alternatively you can use the summary function:
CV Misclassification Rate
We can easily convert the number of misclassification to an error rate:
# Index of tree with minimum error
min.idx <- which.min(cv.ctree$dev)
# Number of misclassifications (this is a count)
(cvmscla <- cv.ctree$dev[min.idx])[1] 9[1] 0.2CV misclassification rate: 9/45 = 0.2
Pros
✅ Easy to interpret and visualize (flowcharts)
✅ Handles categorical and numeric predictors
✅ captures non-linear decision boundaries
✅ automatic feature selection
✅ fast and easy to implement
Cons:
❌ tend to overfit the training data
❌ sensitive to small changes in the data
❌ may not have high predictive accuracy
❌ have difficulty in modeling smooth relationships
❌ greedy approach may not lead to optimal tree

ISLR Fig 8.7 (top). A 2D classification example in which the true decision boundary is linear, and is indicated by the shaded regions. A classical approach that assumes a linear boundary (left) will outperform a decision tree that performs splits parallel to the axes (right).

ISLR Fig 8.7 (bottom): Here the true decision boundary is non-linear. Here a linear model is unable to capture the true decision boundary (left), whereas a decision tree is successful (right).
Comments
We have assumed that the predictor variables take on continuous values. However, decision trees can be constructed even in the presence of qualitative predictor variables.
A split on a categorical variable amounts to assigning some of the qualitative values to one branch and assigning the remaining to the other branch.