Data 311: Machine Learning
Lecture 8: Cross Validation and Data Splitting
University of British Columbia Okanagan
Introduction
In this lecture we’ll be looking at a resampling method called cross validation (or CV for short)
This technique will be used for validating/accessing our model by providing an estimate of model performance on unseen data (i.e. not used in training).
By the end of this lecture, you should understand the difference between training, validation, and test datasets, the need for these splits, and how to implement CV.
Metrics for Model Assessment
For regression we aim to reduce the test MSE \[MSE = \frac{1}{m} \sum_{i=1}^m (y_i-\hat y_i)^2\]
For classification we may consider the test error rate \[\frac{1}{m} \sum_{i=1}^m I(y_i \neq \hat y_i)\]
Where \(1, \dots, m\) denotes unseen test observations that not used in the model-fitting process.
Recall
Ideally, we could fit our model on a sample of data, and then compare the predictions from the estimated model on a very large data set (not used in fitting) to estimate the MSE1.
If we only have one sample, we often split it into a training set (used to fit the model) and testing set (used to estimate the test MSE).
This train/test split approach is sometimes referred to validation approach.
Training vs Test-set Performance

Recall: training error rate often is quite different from the test error rate [Image source]
Validation Approach
Train/Test Split
tr.ind
2, 3, 4, 6, 7, 8, 9, 10, 11, 14, …
te.ind
1, 5, 12, 13, 15, 18, 24, 31, …
In this case, we fit the model with samples with index tr.ind and estimate the MSE using samples with index te.ind
Validation Approach Schematic

A schematic display of the validation set approach. A set of N observations are randomly split into training set (shown in red, containing \(n\) observations 2,3,4,6,7,8,9,10,11,14,…, among others) and a validation set (shown in blue, containing \(m\) observation 1, 5, 12, 13, 15, 18, 24, 31, 33, among others). The ML method is fit on the training set, and its performance is evaluated on the validation set.
Can you think of any limitations/issues with this this method?
ISLR Train Test Figure
jump forward to cross-validation approach

ILSR Fig 5.2 Compares linear vs. higher-order polynomial terms in Linear Regression Left: Validation error estimates for a single split into training (196 obs.) and validation (196 obs.) sets. Right: The validation method was repeated ten times, each time using a different random split of the observations into a training set and a validation set. This illustrates the variability in the estimated test MSE from this approach applied to the Auto data set.
Validation Approach: some problems
High Variance: Results depend heavily on how the data is split.
Inefficient Use of Data: Less data is available for training, especially with small datasets.
Overfitting Risk: The model may overfit to the validation set.
No Separate Test Set: Leads to biased performance estimates.
Single Evaluation: One run may not reflect true generalization.
Data leakage: the model “learns” from data it shouldn’t have access to during training which may lead to overly optimistic performance estimates
Resampling Methods
Solution: training-validation-test split with multiple evaluations.
While we typically don’t have of multiple sets of data, we can fudge it using resampling methods which involves:
- repeatedly drawing samples from a training set
- refitting a model of interest on each sample
Bonus: this will provide additional information about the fitted model that we would not otherwise get.
Wikipedia Definition
- The model is initially fit on a training data set
- Successively, the fitted model is used to predict the responses for the observations in the validation data set.
- Finally, the test data set1 is used to provide an unbiased evaluation of a final model fit on the training data set.
⚠️ The ISLR textbook makes no distinction between the test set and validation set.
Test/Validation/Test
All the data
- Split the data into training, validation, and test sets (a common choice for this might be 70-10-20)
Training
valid.
test
Hide the Test set
Train, tune, and model-select with these:
Training
valid.
Used only after tuning/selection. Used to provide an unbiassed estimate of how well the model generalizes
test
Train, tune, and model-select with these:
Training
valid.
But this is still just one evaluation! We want to be able to do this multiple times. So we do something like this…
K-fold Cross-Validation
Training\(_1\)
valid.\(_1\)
Training\(_2\)
valid.\(_2\)
Train\(_2\)
Training\(_3\)
valid.\(_3\)
Training\(_3\)
Training\(_4\)
valid.\(_4\)
Training\(_4\)
Training\(_5\)
valid.\(_5\)
Training\(_5\)
Training\(_6\)
valid.\(_6\)
Training\(_6\)
Train\(_7\)
valid.\(_7\)
Training\(_7\)
valid.\(_8\)
Training\(_8\)
Steps of K-fold CV
Step 0: Divide dataset into \(k\) equal-sized “folds”; each fold is used as a validation set once, while the remaining folds form the training set
1st iteration: The first fold (in blue) is used as validation set\(_1\), while the remaining folds are used for training the model. The performance of the model on this validation fold is recorded as Performance₁.
2nd iteration: The second fold is used as validation set\(_2\), and the others for training. This gives Performance₂.
The process repeats for all \(k\) folds, each time using a different fold as the validation set, while the rest are used for training.
CV Performance

After completing all \(k\) iterations, the performances from each fold are averaged to get a more reliable estimate of the model’s performance across different subsets of the data. Source of image: [Zitao’s Web]
Retrain
Once we select a model from cross validation, we may want to retrain the model on the complete non-test samples (since combining the training and validation dataset can produce a better model since we have more data)
Training
valid.
test
Re-training selected model
test
Final model testing
Once we have refitted the selected model on the non-test examples, we use the test dataset for unbiased final evaluation (e.g. \(MSE_{test}\) or test error)
The test dataset, untouched until now, estimates model performance on unseen data and checks for overfitting1.
The test dataset used for evaluation is independent from the validation sets we used in cross validation.
Summary of steps
- Training Phase: Use Resampling Methods to obtain multiple training sets to train candidate models.
- Model Evaluation: Instead of evaluating candidates once, evaluate each model multiple times with different validation sets.
- Model Selection: Choose the best performing model based on the average validation scores.
- Retrain: Combine training and validation sets (non-test set) for final training.
- Final Model Testing: Evaluate the model’s performance on the test dataset
Resampling Methods
\(k\)-fold cross-validation (CV) is one of the most commonly used resampling methods
Resampling methods involve repeatedly drawing samples from a dataset and training the model on different subsets of data to evaluate its performance.
Another popular choose is Leave-one-out CV
Next lecture we’ll discuss another resampling method called the bootstrap
Leave One Out Cross-Validation
Leave One Out Cross-Validation (LOOCV) is a special case of \(k\)-fold CV; namely, where \(k\) equals the number of data points in the dataset.
The dataset is split into \(n\) folds, where \(n\) is the number of data points.
In each iteration, 1 data point is used as the validation set, and the remaining \(n-1\) data points are used as the training set.
LOOCV approach
Full sample index (1, 2, … , 200) is systematically divided into:
Index
|
||
|---|---|---|
| CV Set | Training | Validation* |
| 1 | 2, 3, 4, ..., 200 | 1 |
| 2 | 1, 3, 4, ..., 200 | 2 |
| 3 | 1, 2, 4, ..., 200 | 3 |
| ... | ... | ... |
| 200 | 1, 2, 3, ..., 199 | 200 |
LOOCV Schematic

A schematic display of LOOCV. A set of n data points is repeatedly split into a training set (shown in red) containing all but one observation, and a validation set that contains only that observation (shown in blue). The test error is then estimated by averaging the n resulting MSE’s. The first training set contains all but observation 1, the second training set contains all but observation 2, and so forth.
LOOCV Steps
Steps:
Create \(n\) training/validation sets, then for each set:
Fit the model to the training set
Use the fitted model from 2. to predict the responses for the observation in the validation set.
Record the validation set error.
The final performance is the average of the performance scores from each iteration.
CV Estimation
If our response is quantitative, our validation set error can be assessed using the MSE.
For LOOCV the MSE corresponds to a single left out observation \(x_i\) will be defined as \(MSE_i = (y_i-\hat y_i)^2\) where \(\hat y_i\) is the prediction found from the \(i^{th}\) fitted model.
We can then estimate the MSE of the model using \[CV_{(n)} = \frac{1}{n} \sum_{i=1}^n MSE_i\]
LOOCV Steps Visualized
| Training Set | Prediction | Metric \(MSE_i\) |
|---|---|---|
| 2,3,4, …, 199, 200 | \(\hat y_1 = \hat f_{1}(x_1)\) | \((y_1 - \hat y_1)^2\) |
| 1,3,4, …, 199, 200 | \(\hat y_2 = \hat f_{2}(x_2)\) | \((y_2 - \hat y_2)^2\) |
| 1,2,4, …, 199, 200 | \(\hat y_3 = \hat f_{3}(x_3)\) | \((y_3 - \hat y_3)^2\) |
| \(\vdots\) | \(\vdots\) | \(\vdots\) |
| 1,2,3, …, 198, 199 | \(\hat y_{200} = \hat f_{200}(x_{200})\) | \((y_{200} -\hat y_{200})^2\) |
Pros to LOOCV
Less bias: LOOCV uses almost all of the data to fit the model whereas the validation approach may only use 50% (which tends to lead to an overestimate of the test error).
Deterministic estimates: LOOCV always gives the same estimate because the partitions are not chosen randomly.
Very general: LOOCV1 can be used with any kind of predictive modeling; logistic regression, LDA, you name it!
Cons to LOOCV
Computationally demanding1: LOOCV requires the model to be fitted \(n\) times which can be very costly if \(n\) is large and/or the model is slow to fit.
More variance since LOOCV estimates are highly correlated2 \[\begin{align} \text{Var}(X + Y) = \text{Var}(X) + \text{Var}(Y) + 2\cdot\text{Cov}(X,Y) \end{align}\]
5-fold Visualization

A schematic display of 5-fold CV. A set of n = 20 observations is randomly split into five non-overlapping groups (or folds). Each of these folds takes a turn a validation set (shown in blue), and the remainder as a training set (shown in red). The test error is estimated by averaging the five resulting MSE estimates.

\(k\)-Fold split
Full Sample Index: 1, 2, … , 20, with \(k = 5\)
| Training Set | Validation* |
|---|---|
| 1, 2, 4, 5, 6, 8, 9, 11, 13, 14, 15, 16, 17, 18, 19, 20 | 3, 7, 10, 12 |
| 1, 3, 5, 6, 7, 8, 9, 10, 11, 12, 13, 15, 16, 17, 18, 20 | 2, 4, 14, 19 |
| 1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 12, 14, 15, 17, 19, 20 | 5, 13, 16, 18 |
| 1, 2, 3, 4, 5, 7, 10, 11, 12, 13, 14, 16, 17, 18, 19, 20 | 6, 8, 9, 15 |
| 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 18, 19 | 1, 11, 17, 20 |
5-fold CV Calculations
| Validation Set \(V\) | Prediction | Metric \(MSE_j\) |
|---|---|---|
| \(V_1\) = 3, 7, 10, 12 | \(\hat f_1 (x_3, x_7, x_{10}, x_{12})\) | \(\frac{1}{4}\sum_{i\in V_1} (y_i - \hat y_i)^2\) |
| \(V_2\) = 2, 4, 14, 19 | \(\hat f_2 (x_2, x_4, x_{14}, x_{19})\) | \(\frac{1}{4}\sum_{i\in V_2} (y_i - \hat y_i)^2\) |
| \(V_3\) =5, 13, 16, 18 | \(\hat f_3 (x_5, x_{13}, x_{16}, x_{18})\) | \(\frac{1}{4}\sum_{i\in V_3} (y_i - \hat y_i)^2\) |
| \(V_4\) =6, 8, 9, 15 | \(\hat f_4 (x_6, x_8, x_{9}, x_{15})\) | \(\frac{1}{4}\sum_{i\in V_4} (y_i - \hat y_i)^2\) |
| \(V_5\) =1, 11, 17, 20 | \(\hat f_5 (x_1, x_{11}, x_{17}, x_{20})\) | \(\frac{1}{4}\sum_{i\in V_5} (y_i - \hat y_i)^2\) |
\[\begin{align} \text{CV}_{(5)} = \frac{1}{5} \sum_{j=1}^5 MSE_j \end{align}\]
\(k\)-Fold Estimation
More generally, we can calculate the MSE for each validation set \(j\), for \(j = 1, \dots, k\) \[MSE_j = \frac{1}{n_j} \sum_{i \in j}(y_i-\hat y_i)^2\] where \(n_j\) is the number of observations in the \(j\)th validation set. A cross-validated estimate the MSE given by \[ CV_{(k)} = \frac{1}{k}\sum_{j=1}^k MSE_j \]
ISLR Cross Validation Figure
jump back to validation approach

ILSR Fig 5.4 Cross-validation was used on the Auto data set in order to estimate the test error that results from predicting mpg using polynomial functions of horsepower. Left: The LOOCV error curve. Right: 10-fold CV was run nine separate times, each with a different random split of the data into ten parts. The figure shows the nine slightly different CV error curves. These are much less variable than the Validation Approach
\(k\)-fold vs. LOOCV
Pros of \(k\)-fold
- Less variance than LOOCV
- More computationally feasible than LOOCV (\(k\) vs. \(n\) model fits)
- Often gives more accurate estimates of test error than LOOCV.
Cons of \(k\)-fold
- more bias than LOOCV when estimating MSE
- Non deterministic estimate of the MSE (randomly spliting the data into \(k\) folds)
Bias-Variance trade-off


LOOCV will have lower bias than does \(k\)-fold CV with \(k < n\), but LOOCV has higher variance.
k-fold or LOOCV?
- k-fold or LOOCV
k-fold or LOOCV?
-
k-fold or LOOCV?1 What value of \(k\) is best?
The ISLR authors argue that for intermediate values of \(k\), say 5 or 10, \(k\)-fold CV provides a better estimate of test error rate than LOOCV2
In other words, the decrease in variance tends to outweigh the increase in bias when we chose 5/10-fold validation over LOOCV.
CV and Classification (LOO)
CV (either \(k\)-fold or LOO) can be applied easily in a classification context as well.
For instance, in LOOCV we can calculate cross-validated misclassification rates by replacing \(MSE_i\) with the validation misclassification rate (aka error rate \(\text{Err}_i\)) : \[ CV_{(n)} = \frac{1}{n} \sum_i^n \text{Err}_i = \frac{1}{n} \sum_i^n I(y_i \neq \hat y_i) \] where \(I(y_i \neq \hat y_i)\) is 1 if the left-out observation was misclassified using the \(i\)th model, and 0 otherwise.
CV and Classification (k-fold)
We divide the data into \(k\) roughly equal-sized parts \(C_1, C_2, \ldots, C_k\) where \(n_j\) is the number of observations in part \(j\): if \(n\) is a multiple of \(k\), then \(n_j = n/k\).
\[\begin{align} MC_j &= \frac{1}{n_j} \sum_{i \in j} I(y_i \neq \hat y_i) \\ CV_{(k)} &= \sum_{j=1}^k \frac{n_j}{n} MC_j \end{align}\]
Model Selection
We have just seen how we could use these methods to to assess model performance.
Now let’s switch gears and see how these methods can be used for model selection.
Now we can use cross-validation (CV) to compare and select the best-performing model among several candidates.
In this case, we use CV to choose which value of
k1 for KNN performs the best in terms of generalization.
iClicker
iClicker:
What is the primary purpose of the training dataset in machine learning?
- To tune the model’s hyperparameters
- To evaluate the final performance of the model
- To train the model on a given dataset
- To prevent overfitting during training
- To train the model on a given dataset
iClicker
iClicker:
What is the key difference between a validation set and a test set?
The validation set is used for final model evaluation
The test set is used for hyperparameter tuning
The validation set is used for hyperparameter tuning, while the test set is for evaluating generalization
The validation set is larger than the test set
- The validation set is used for hyperparameter tuning, while the test set is for evaluating generalization
iClicker
iClicker:
Which of the following best describes the concept of data leakage
A. Including irrelevant features in the training set B. Sharing test data with the training data C. Training on a small portion of data D. Using a non-random dataset split
- Sharing test data with the training data
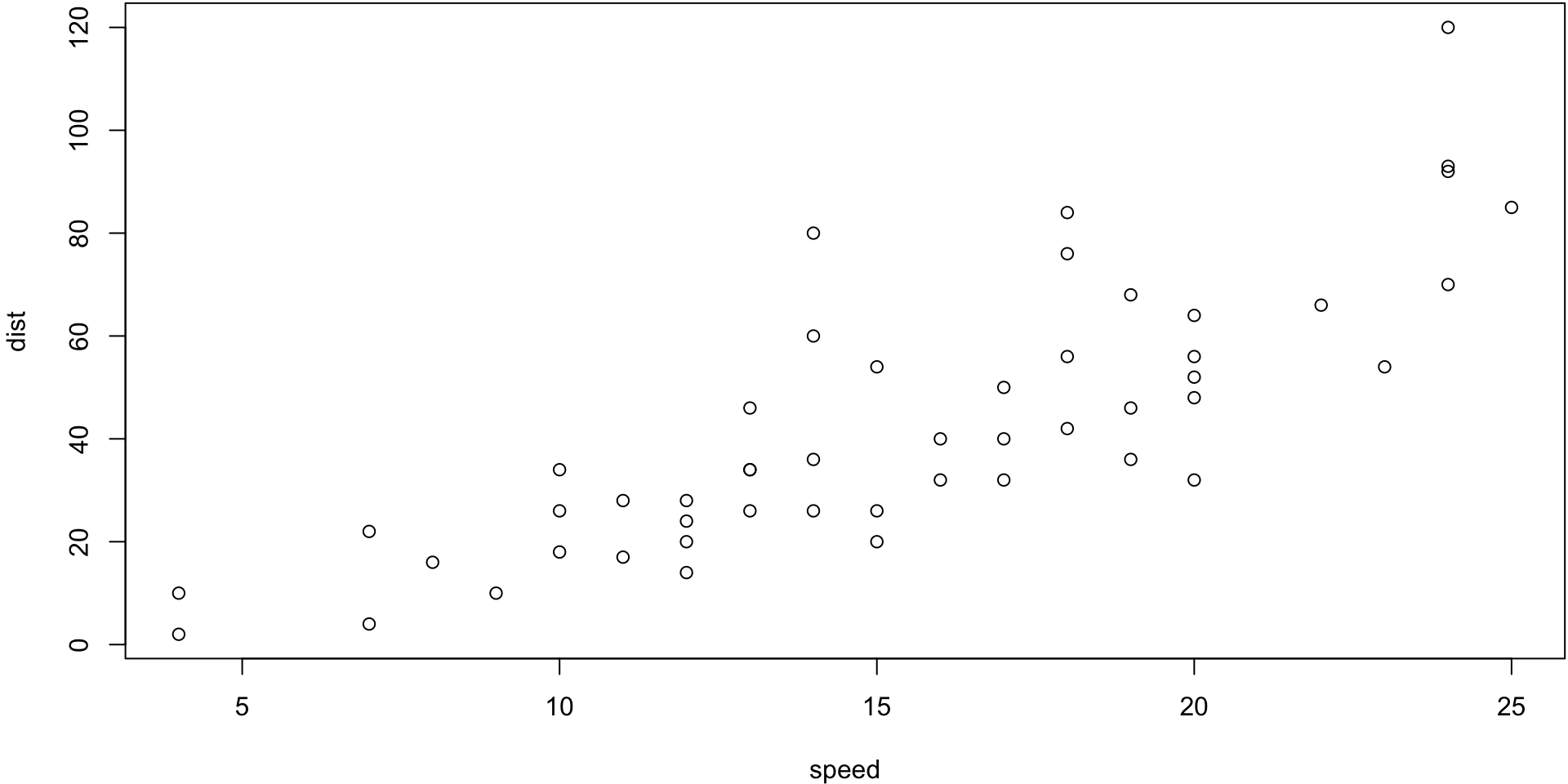
Cars Example
The cars data give the speed of 1920s cars (speed) and the distances taken to stop (dist).
KNN (from FNN package)
-
trainmatrix or data frame of training set cases. -
testmatrix or data frame of test set cases. A vector will be interpreted as a row vector for a single case. If not supplied, LOOCV will be done. -
yreponse of each observation in the training set. -
knumber of neighbours considered.
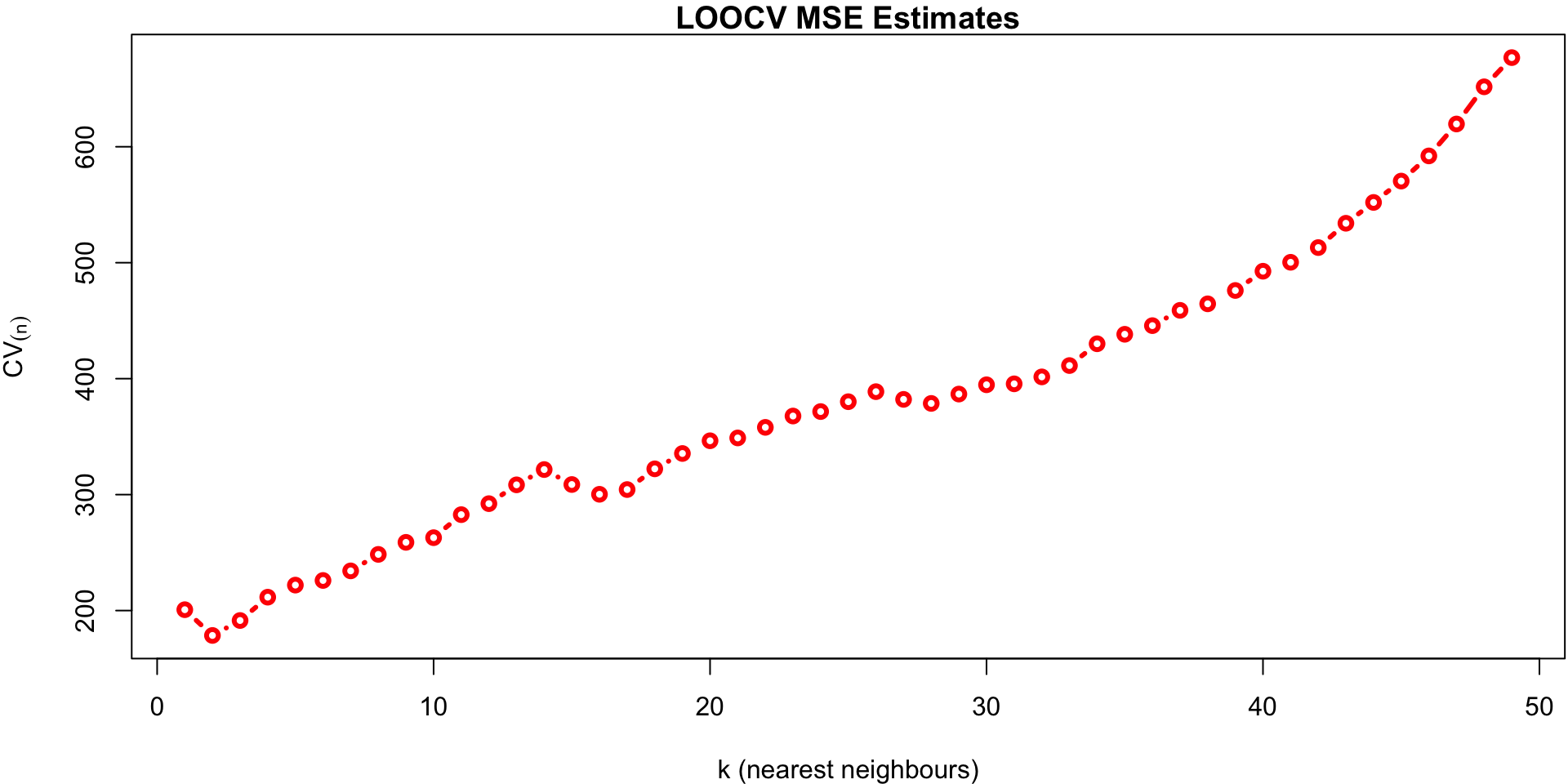
Cross-validated estimates
We fit all possible
kvalues (1 to 49 - the number of samples)If we don’t supply a test test,
knn.regperforms LOOCVWe plot the cross-validated estimates of MSE across all values of
keach calculated using: \[CV_{(n)} = \frac{1}{n} \sum_{i=1}^n MSE_i\]
k vs MSE plot
library(FNN)
data(cars, package="datasets")
attach(cars)
kr <- list()
predmse <- NA
for(i in 1:49){
# LOOCV (default if no test set is supplied)
kr[[i]] <- knn.reg(speed, test=NULL, dist, k=i)
predmse[i] <- kr[[i]]$PRESS/nrow(cars) # LOOCV estimate for k = i
}
par(mar = c(4, 4.2, 1.1, 0.1))
plot(predmse, type="b", lwd=3, col="red",
ylab = expression(CV[(n)]),
xlab = "k (nearest neighbours)",
main ="LOOCV MSE Estimates")
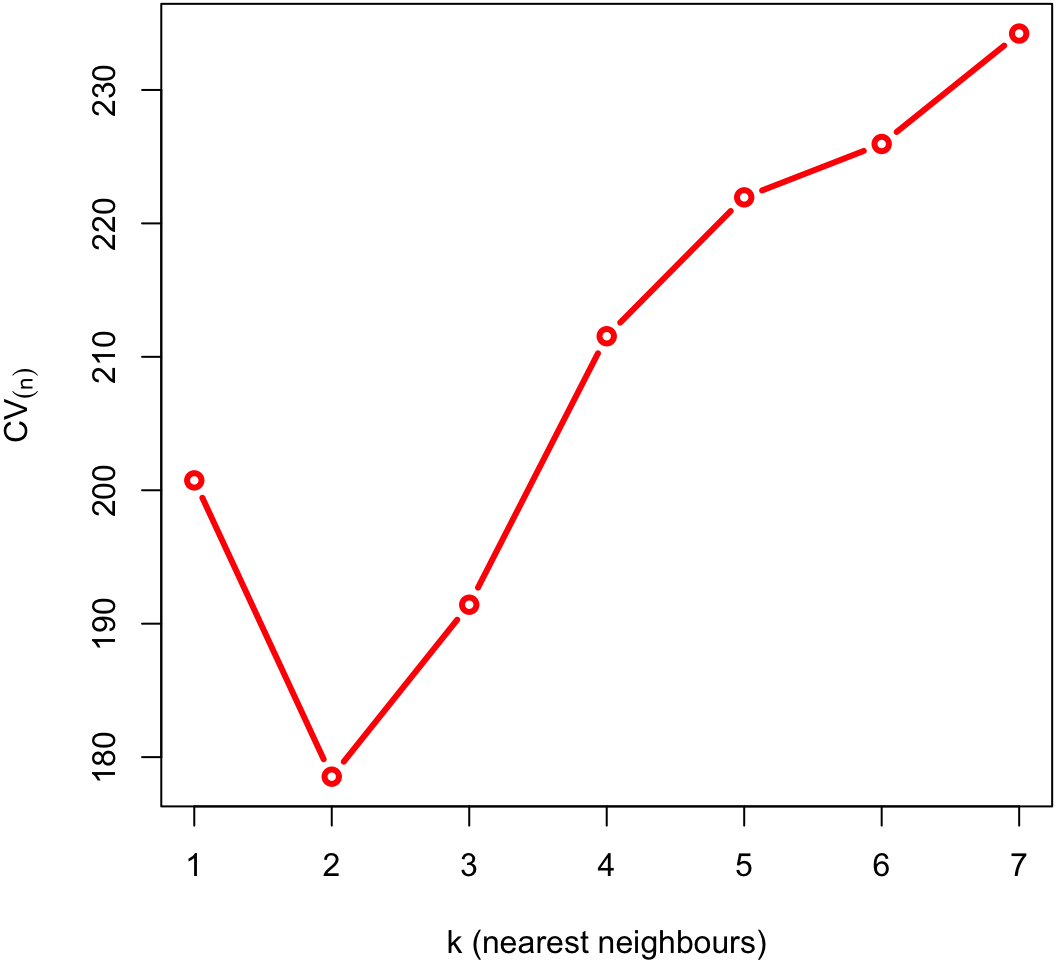
k vs MSE plot
Zoomed in
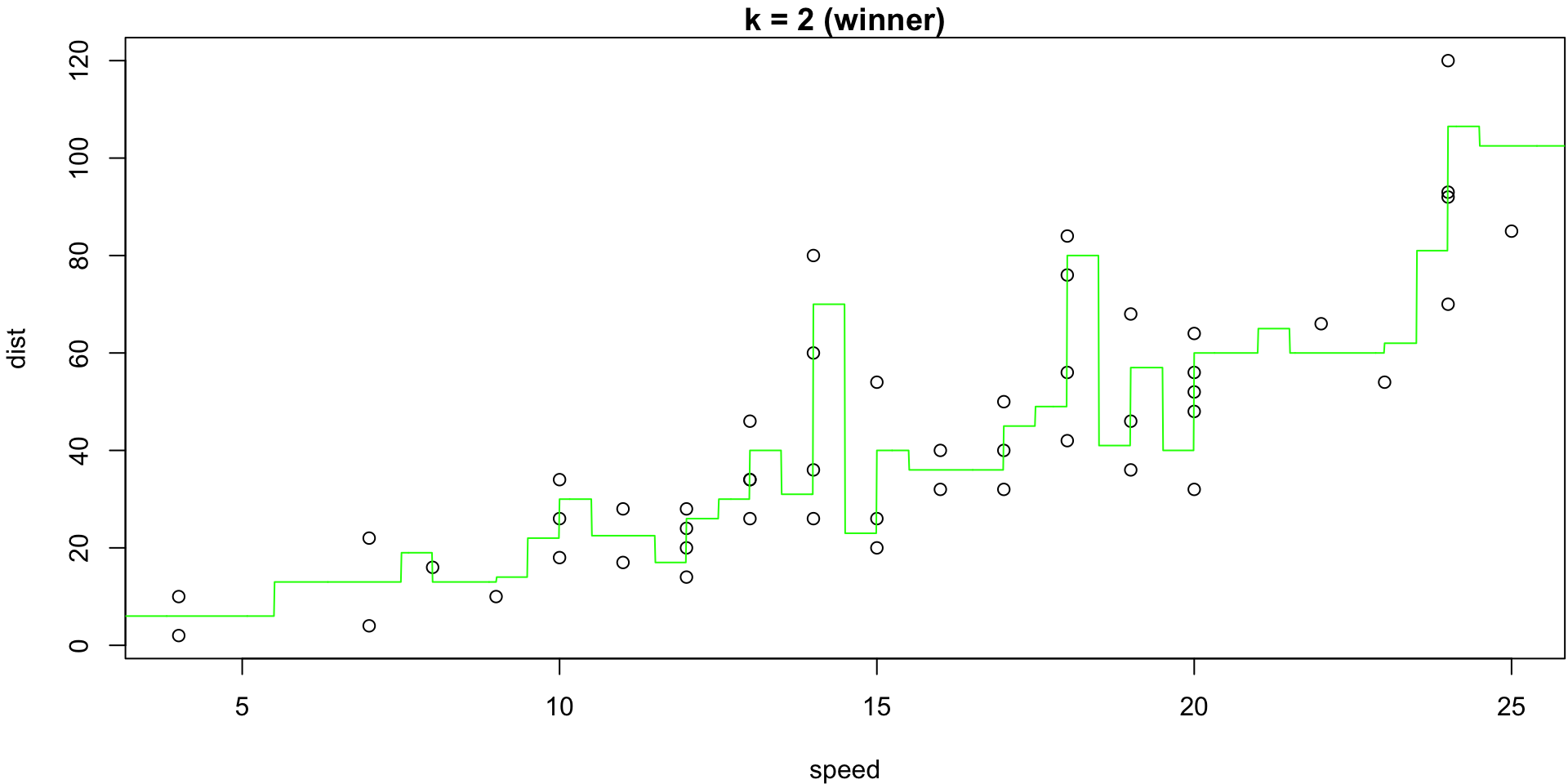
The minimum of that plot suggests that the best value of k is at 2.
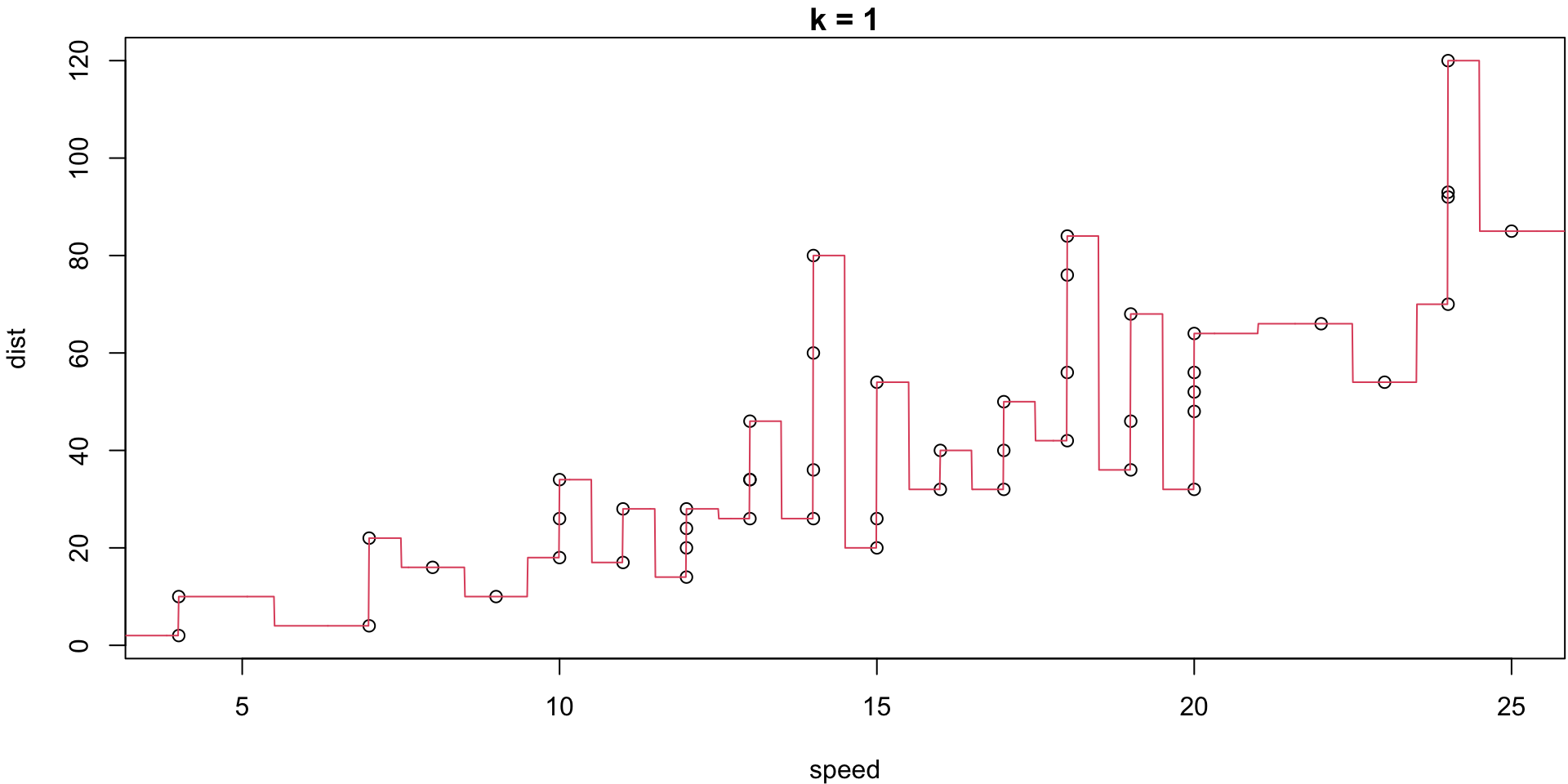
k = 1
k = 5
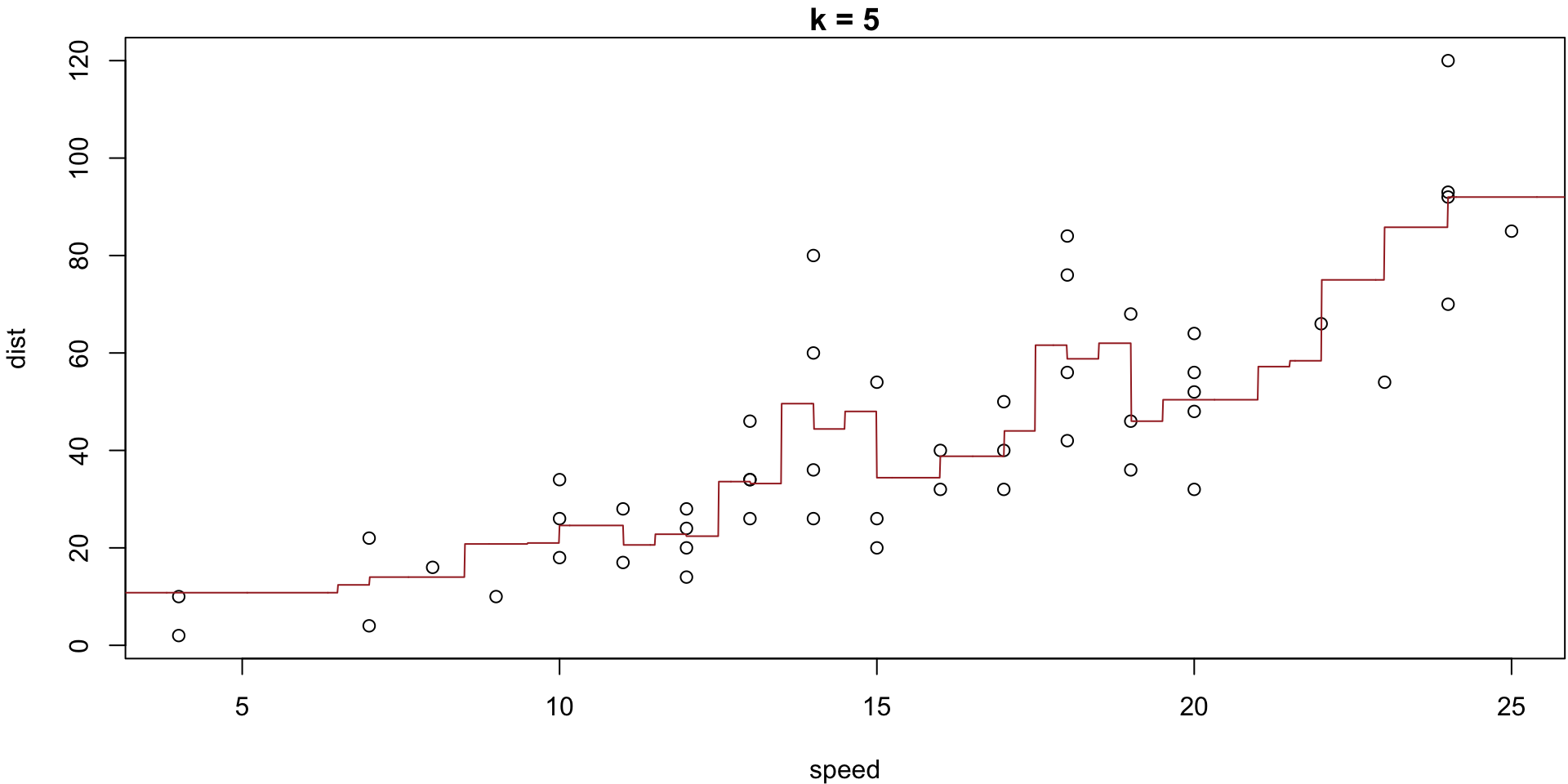
k = 10
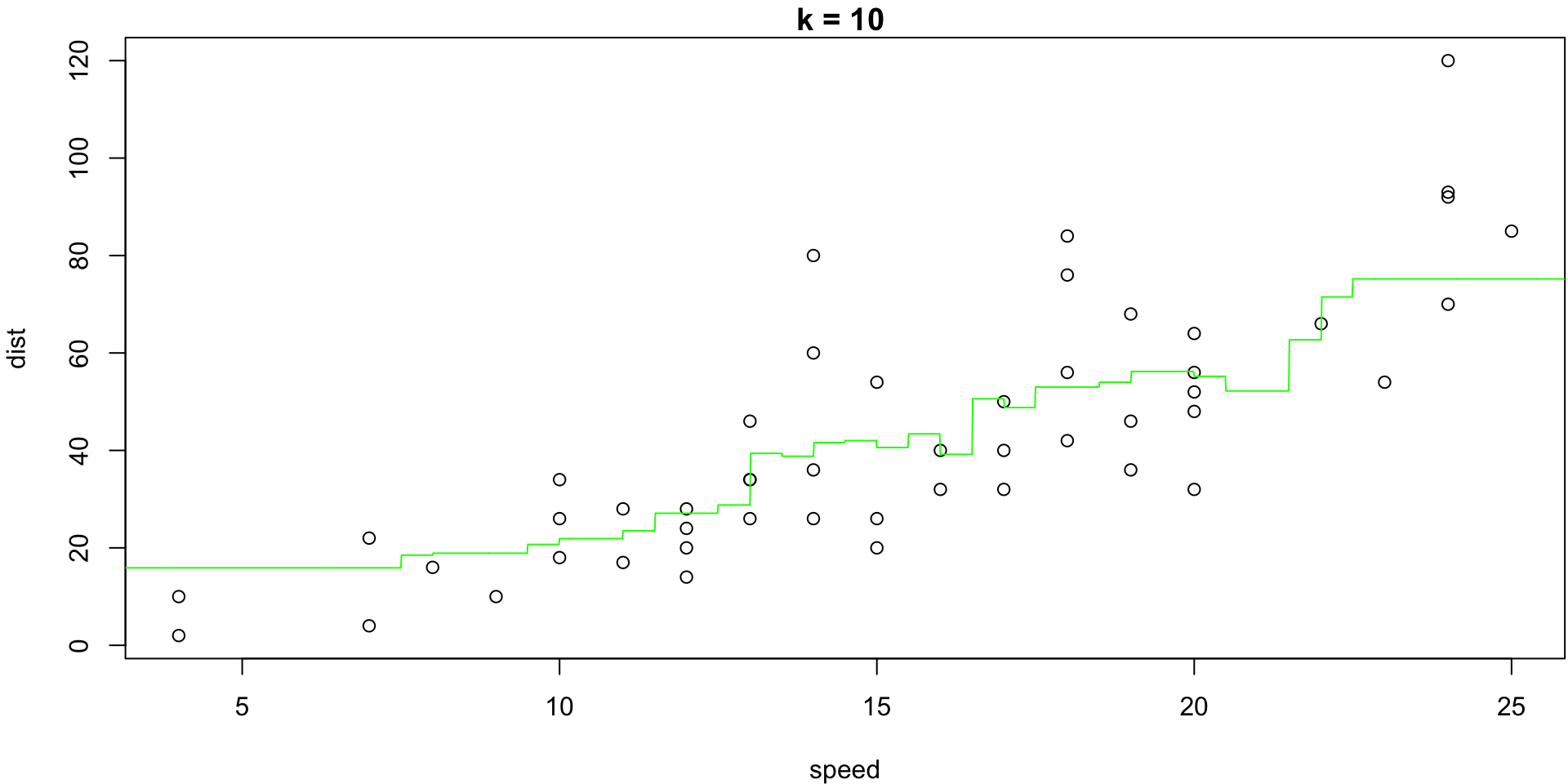
k = 20
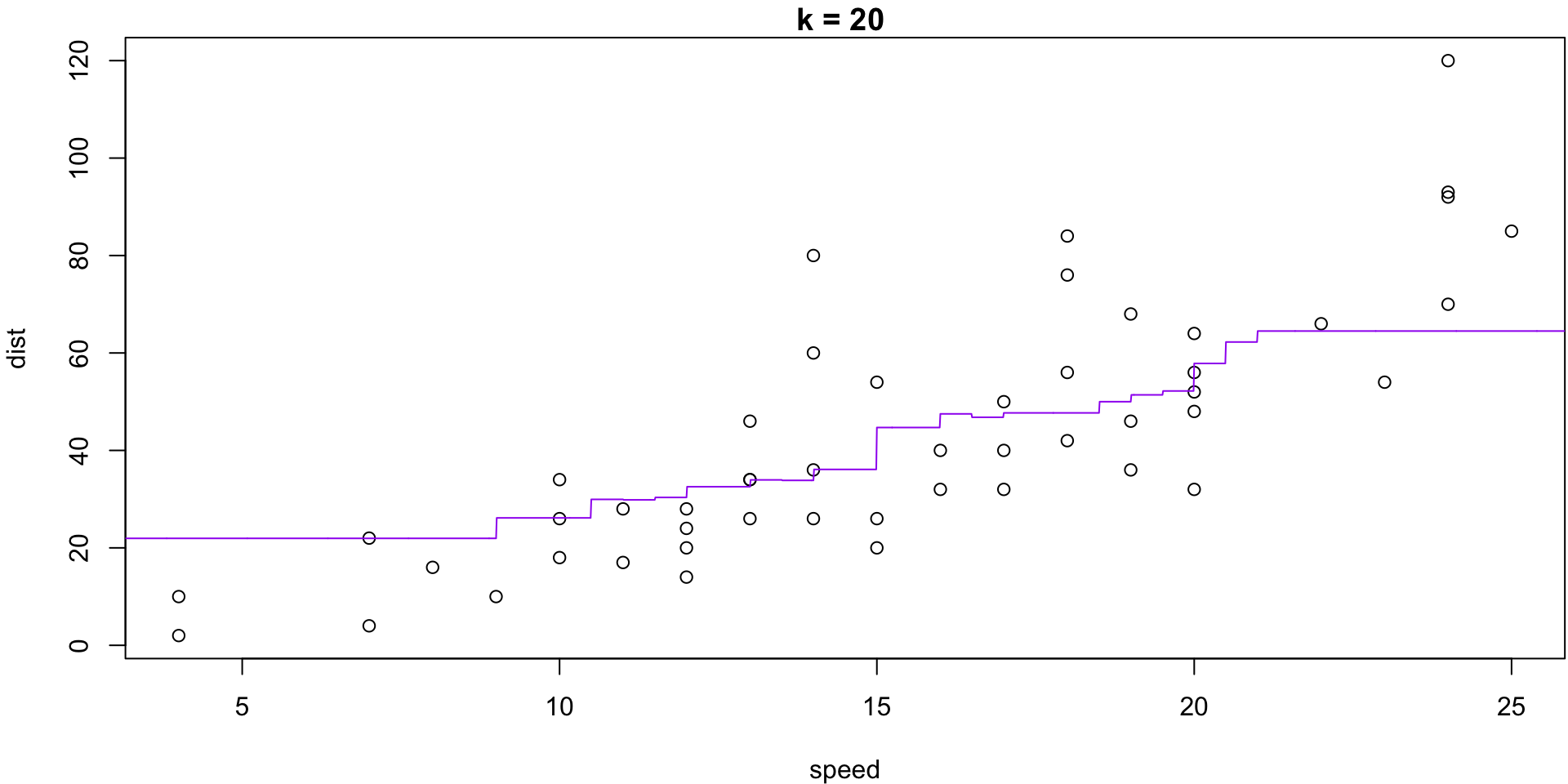
k = 2 (winner)
Comparing Models
Not only can we select
kusing CV, but we can furthermore compare that best KNNreg model’s predictive performance with any other potential model.Since CV estimates the MSE, there’s no reason we cannot provide that estimate in the context of, say, simple linear regression…
Cars example (regression)
Car data, simple linear regression on full sample
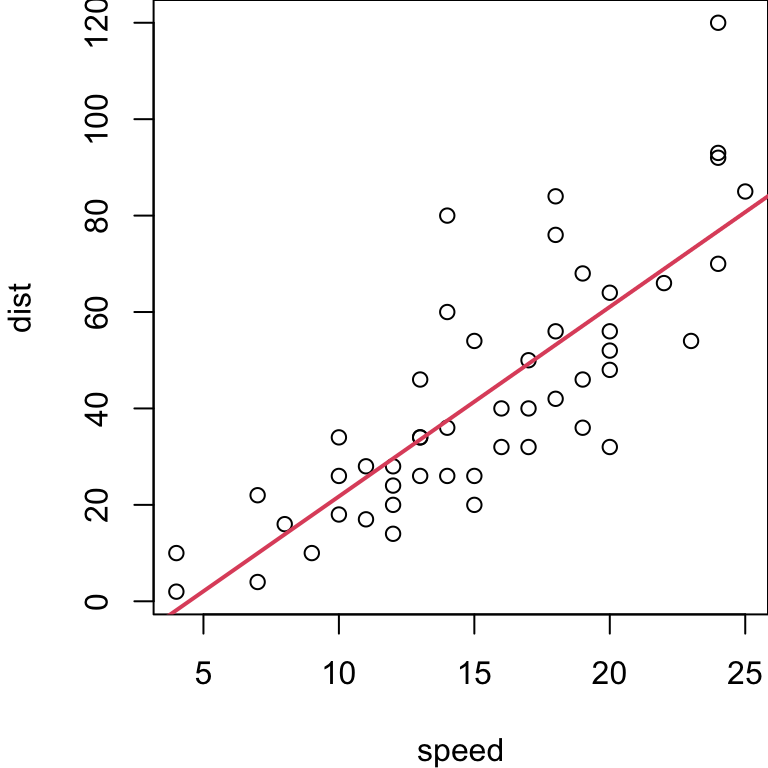
...
Call:
lm(formula = dist ~ speed)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.5791 6.7584 -2.601 0.0123 *
speed 3.9324 0.4155 9.464 1.49e-12 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 15.38 on 48 degrees of freedom
Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
...Regression MSE estimate
Under the inferential assumptions for SLR, we have a theoretical (unbiased) estimate of the test MSE via \[ \hat{\text{MSE}} = \frac{\text{RSS}}{n-2} = \frac{\sum (y_i - f(x_i))^2}{n-2}\]
For the
carsdata, that gives us: \(\frac{11353.52}{48}= 236.53\)In this case
k= 2 KNN model gets a CV MSE estimate of 178.54 hence is suggested as the better model.
LOOCV Regression Shortcut
While we could compare these estimates of MSE directly, we could go one step further and get the CV estimate for MSE by applying LOOCV to the linear model!
Notably, there is a mathematical shortcut for LOOCV with the least squares linear or polynomial regression that calculate \(CV_{(n)}\) using a single fit!
The details of this shortcut are discussed in Section 5.1.2 of the ILSR textbook (we won’t go over them here).
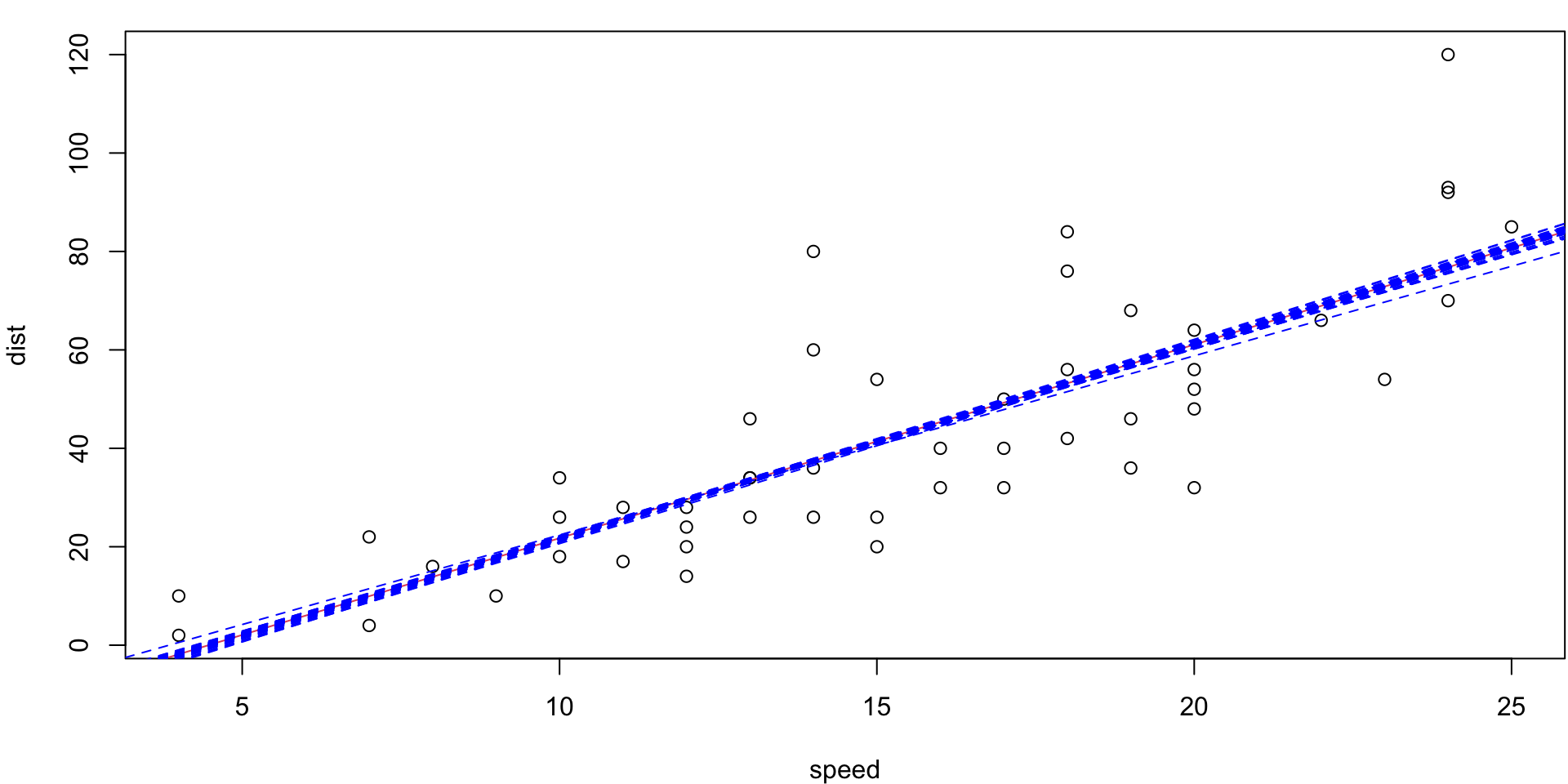
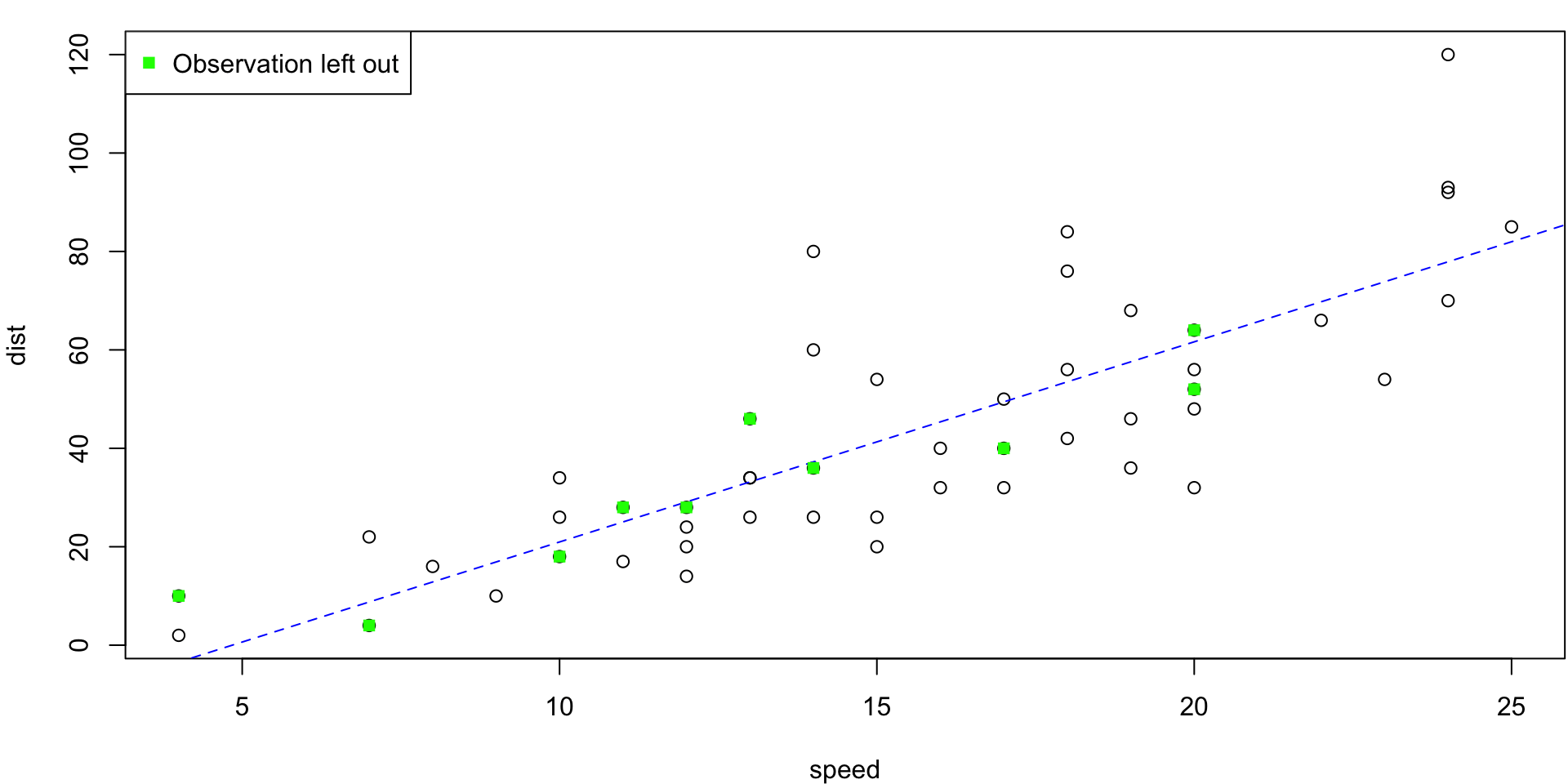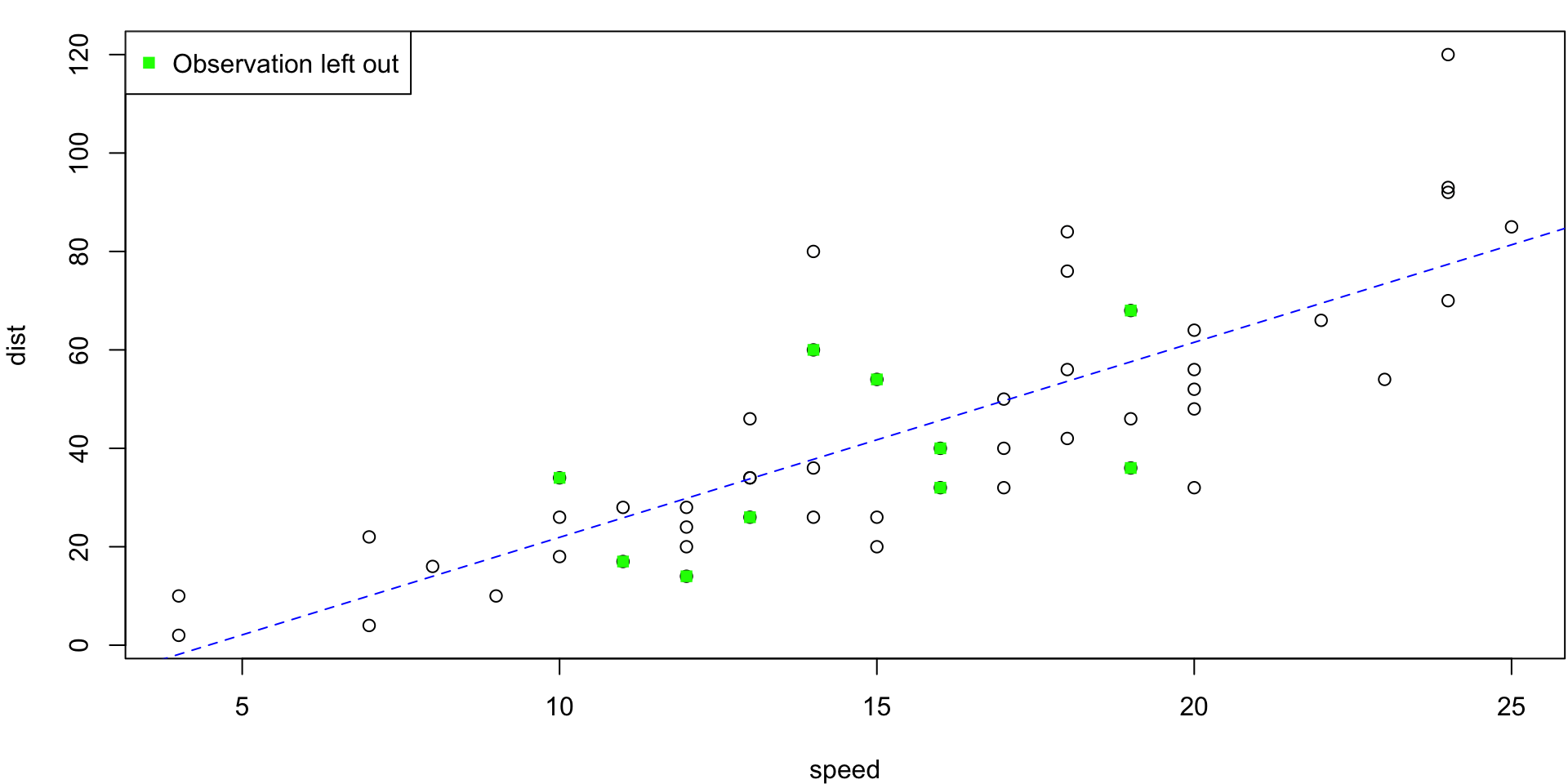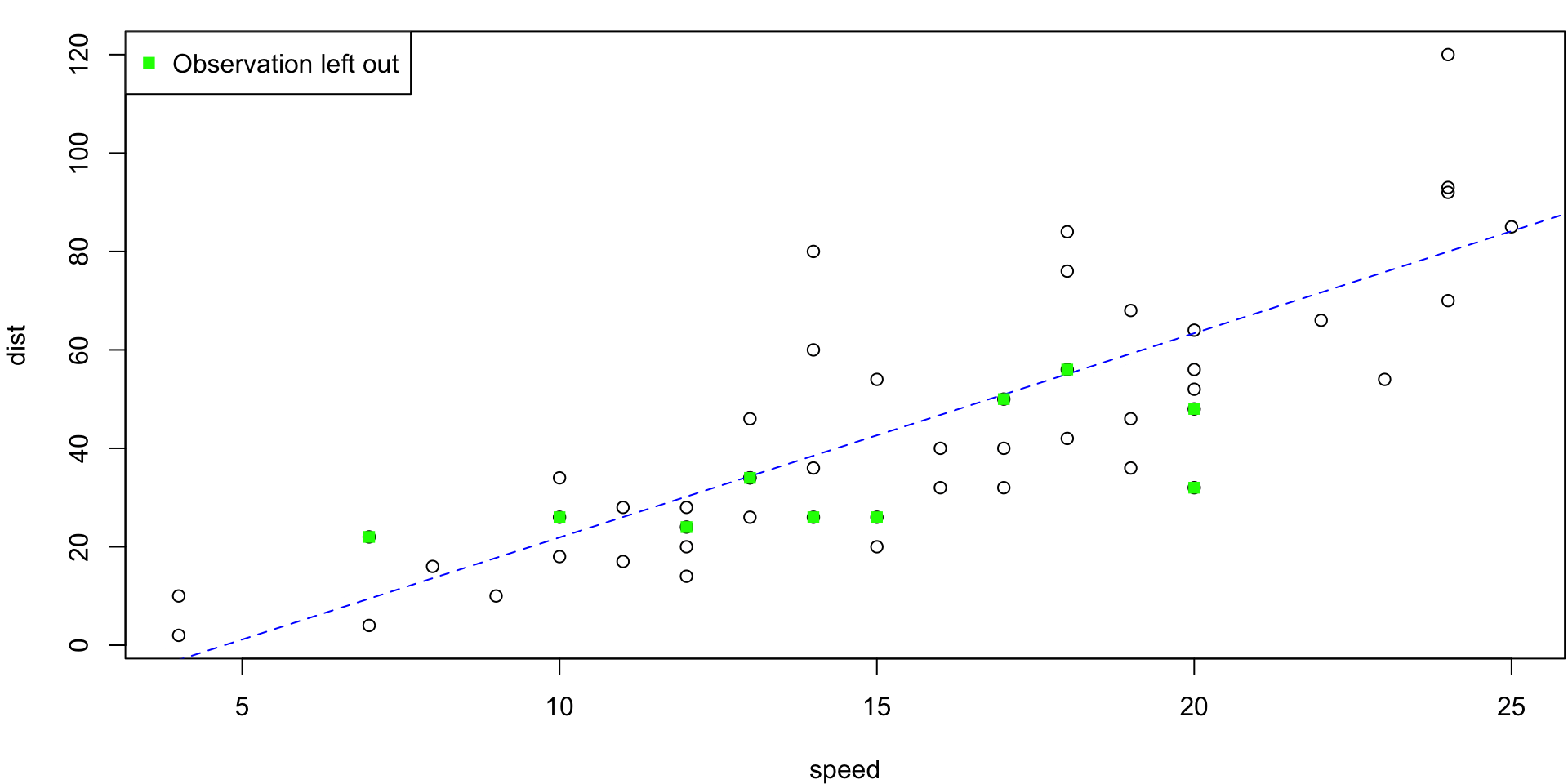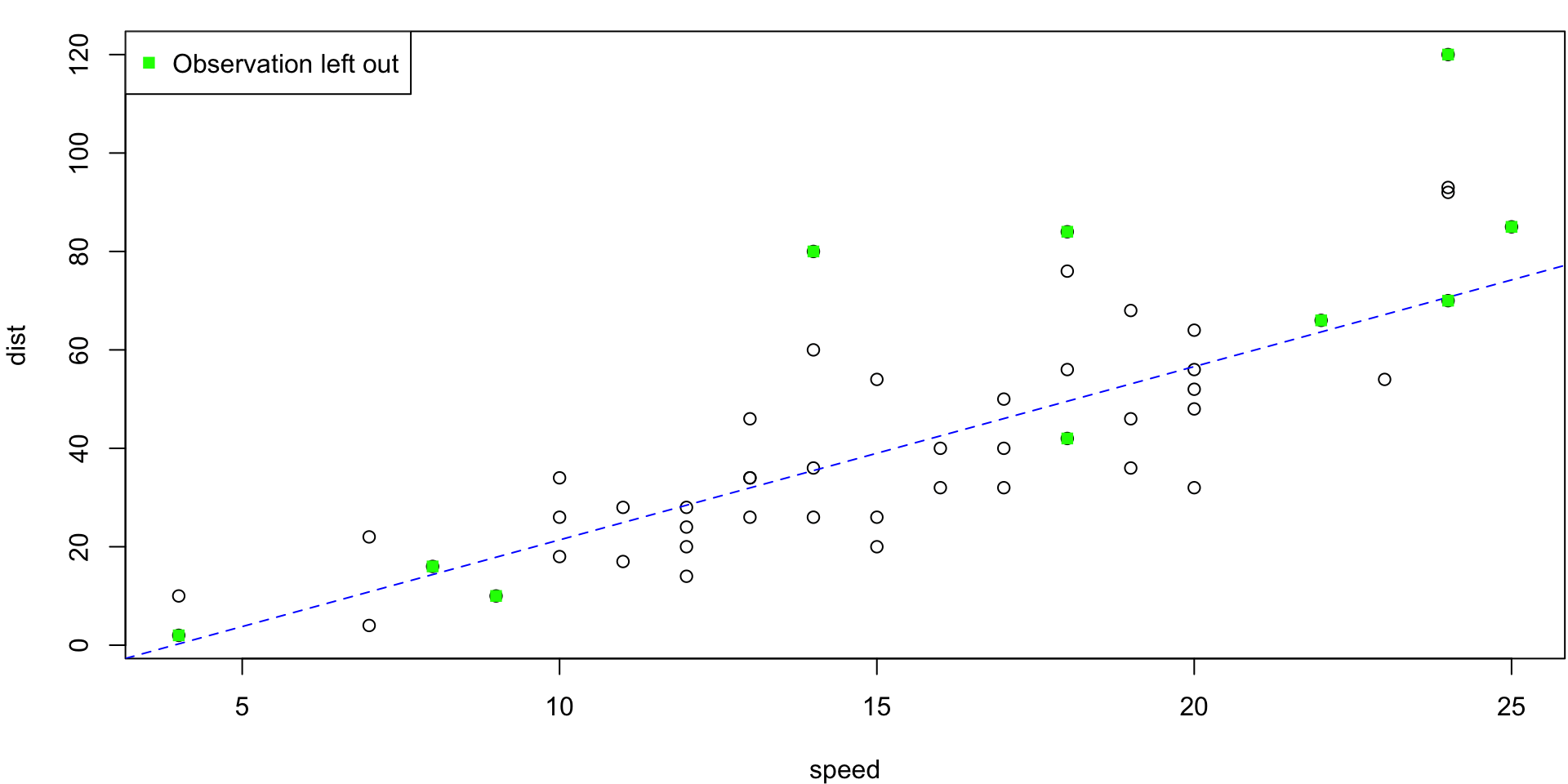
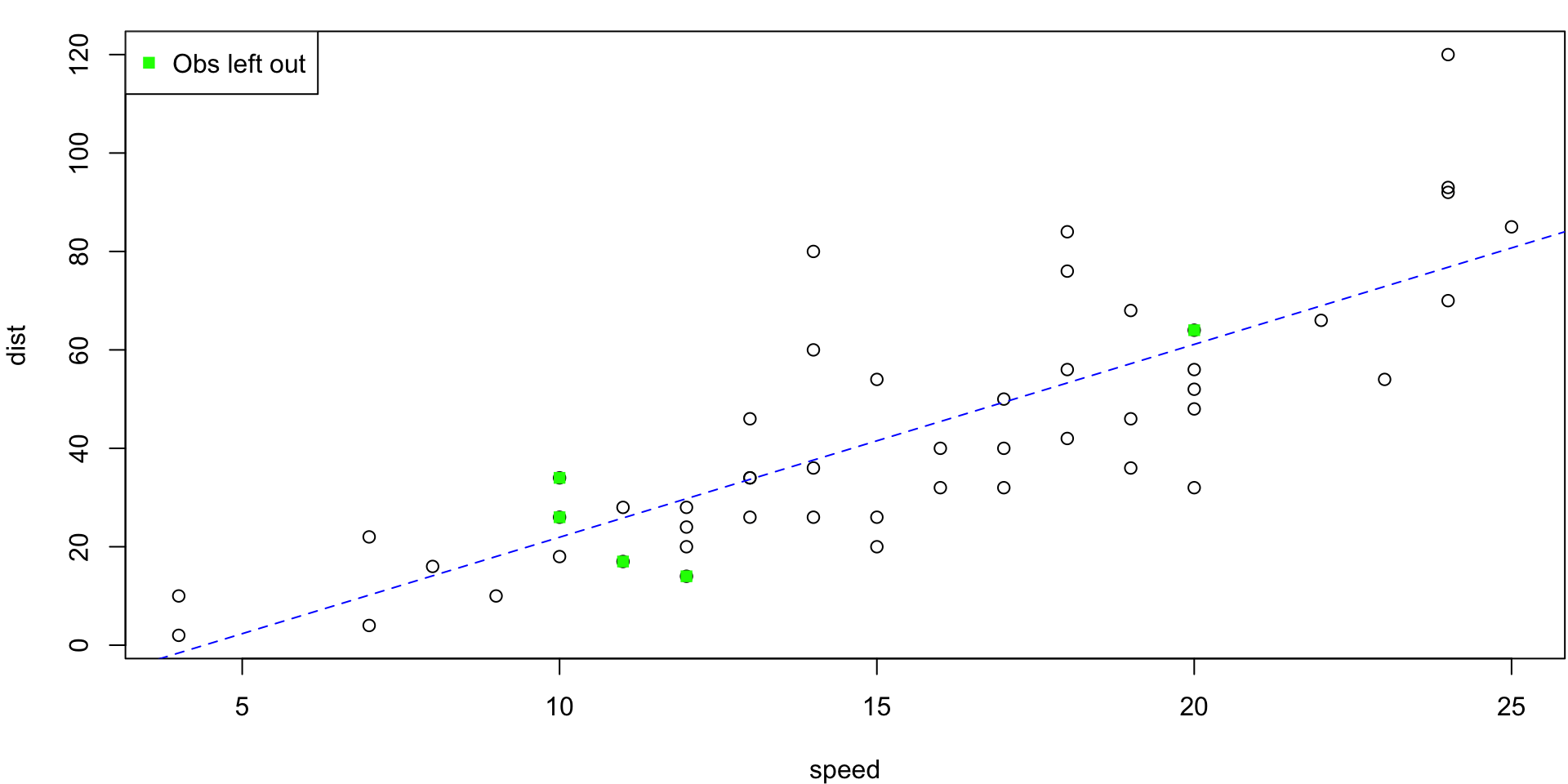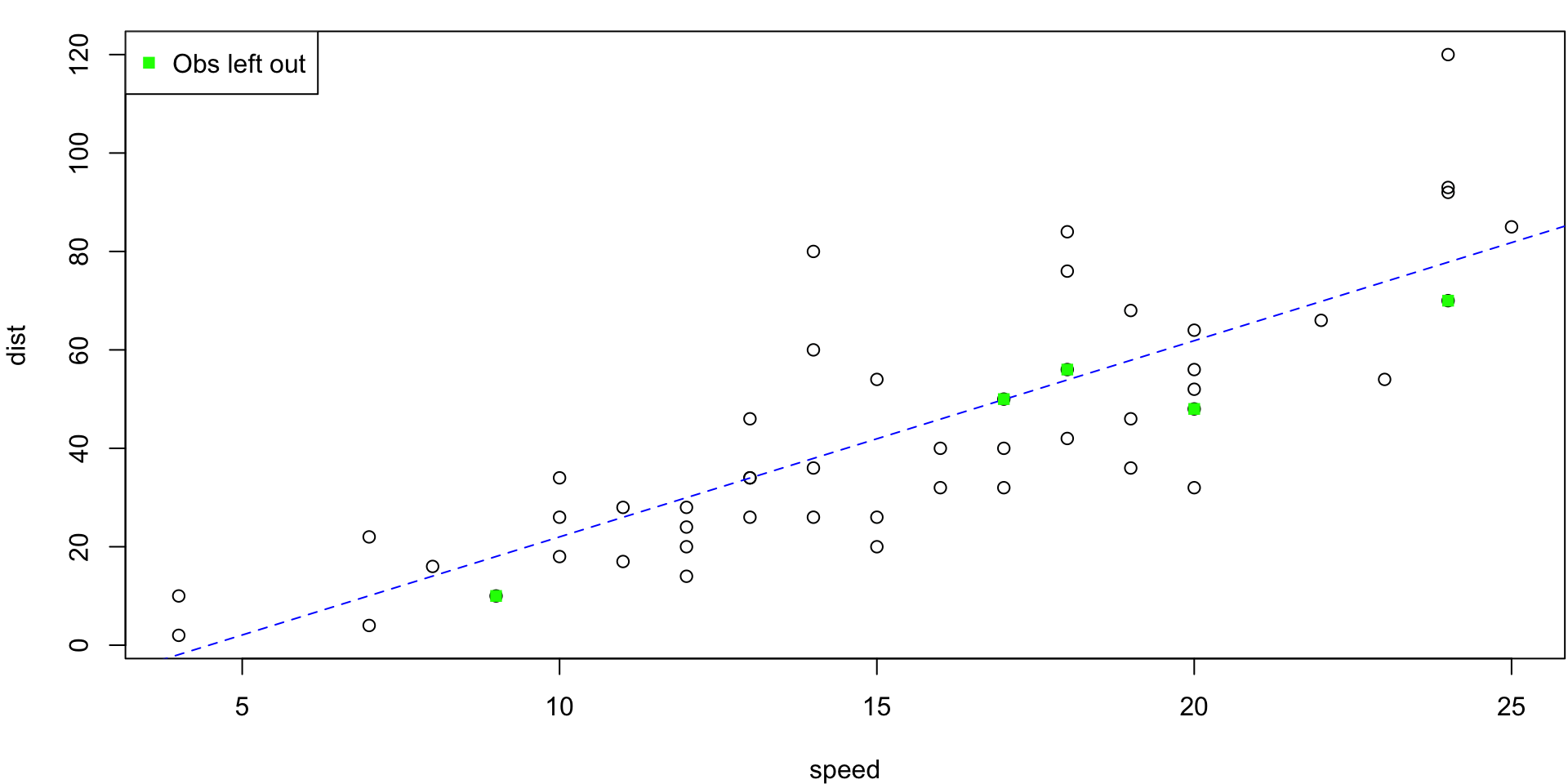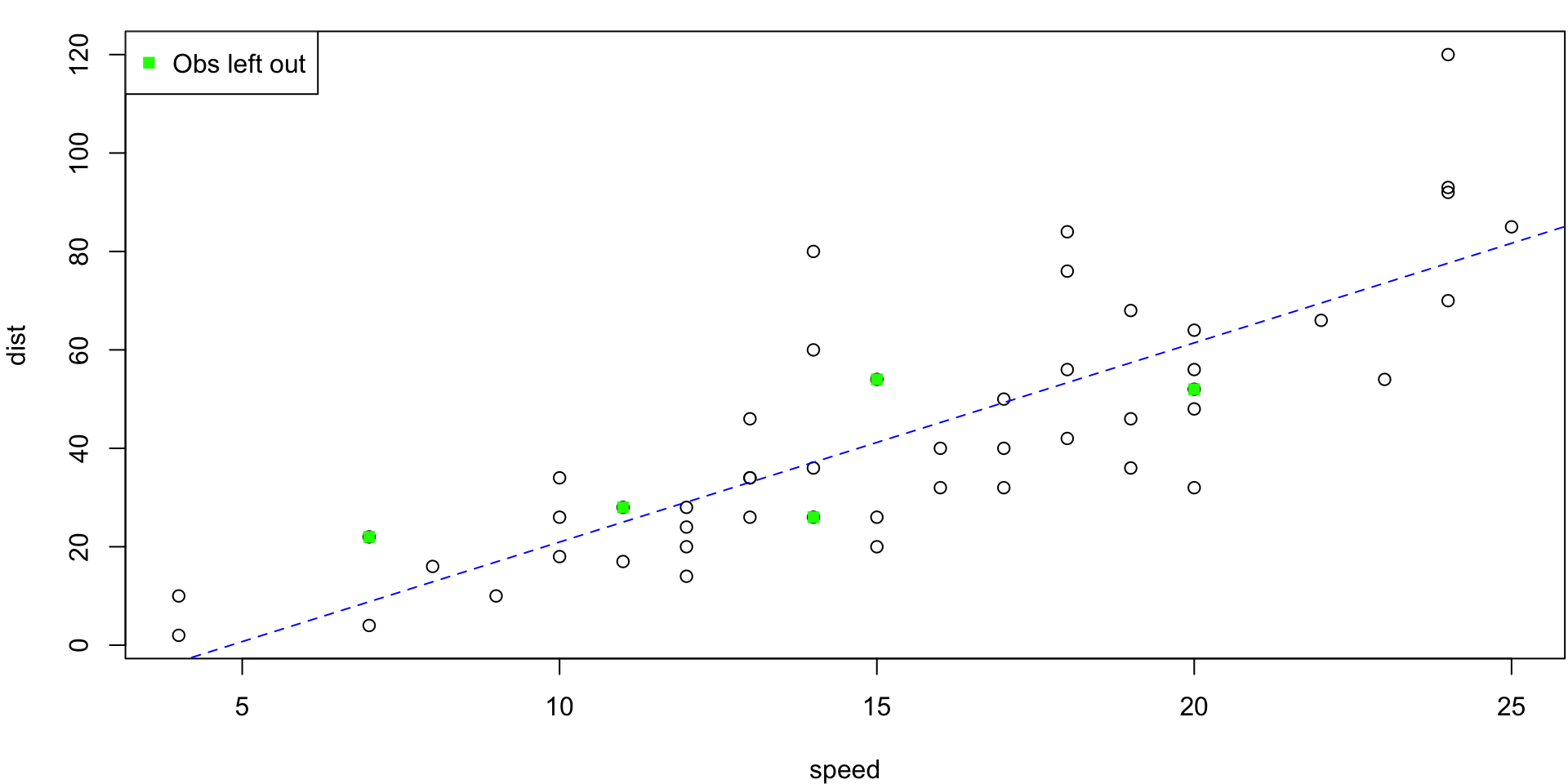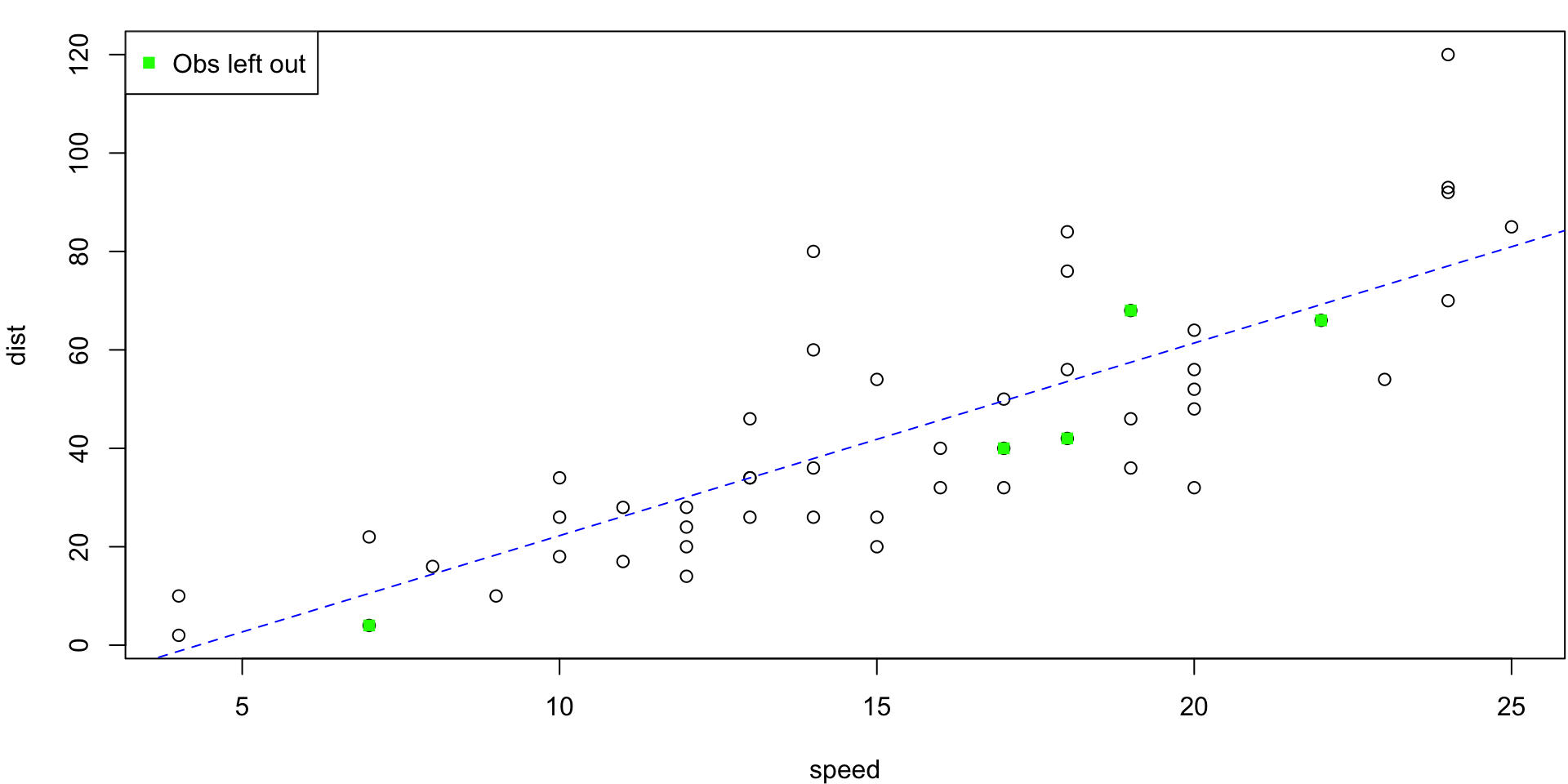
LOO Regression Animation
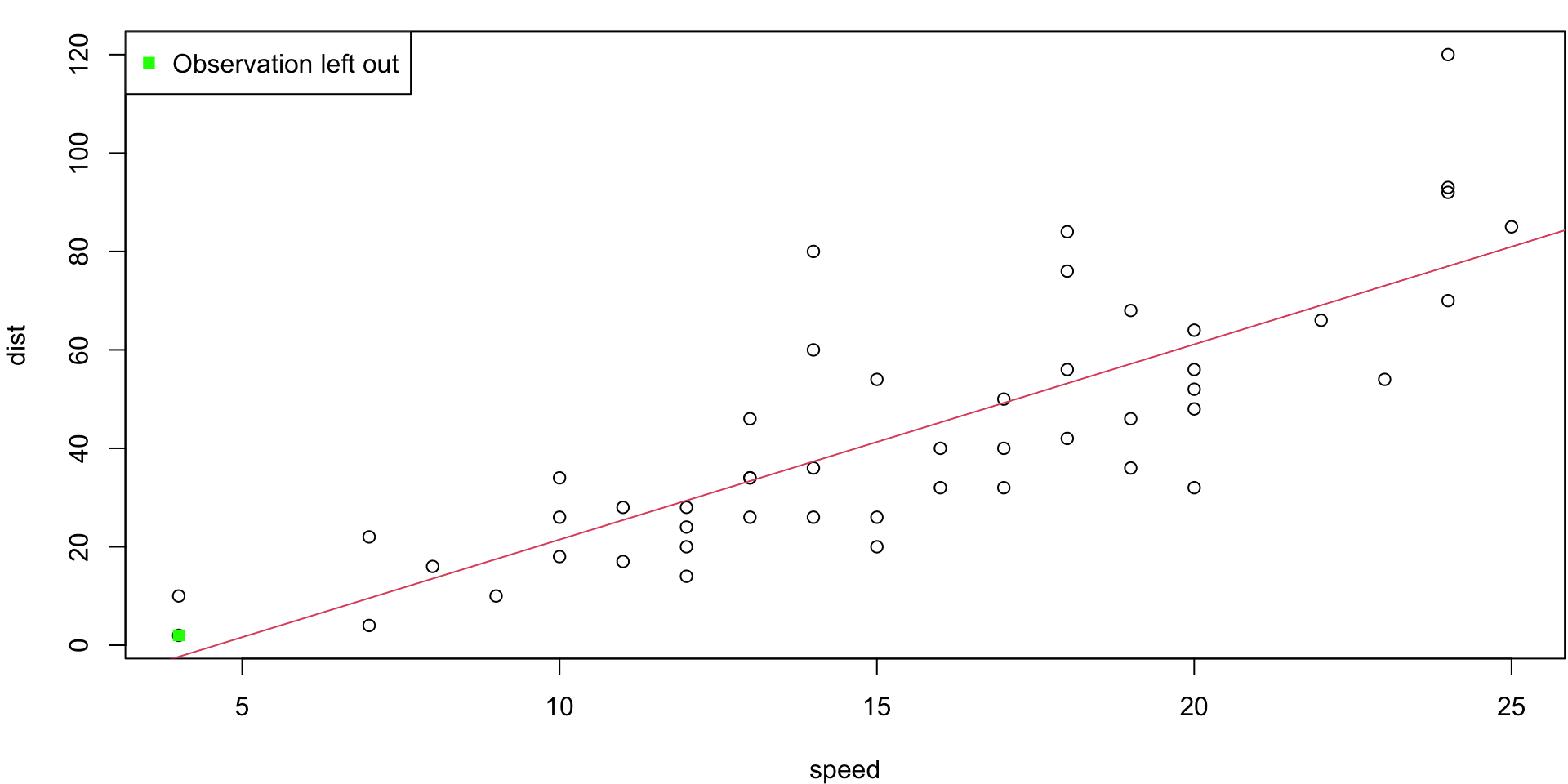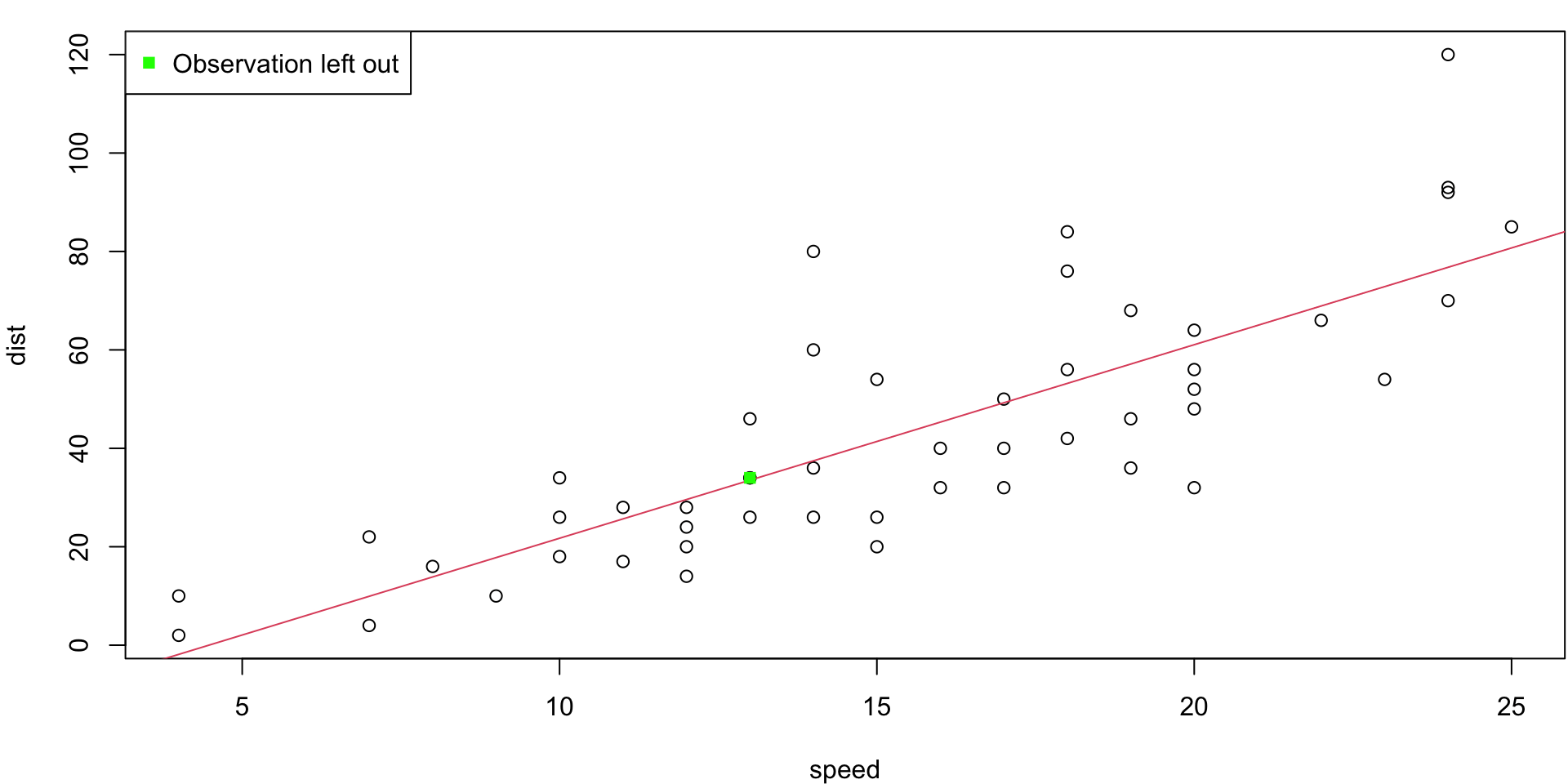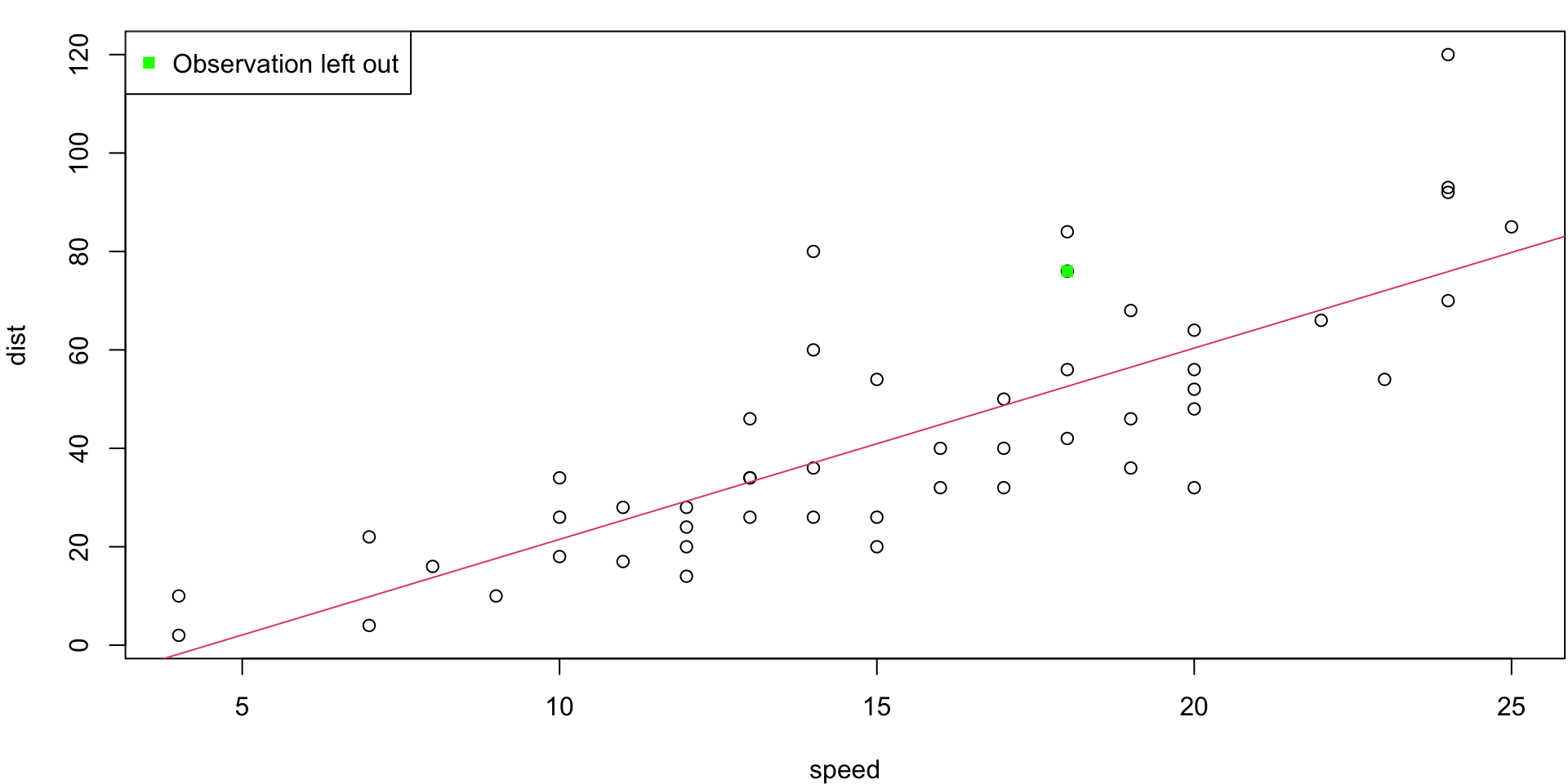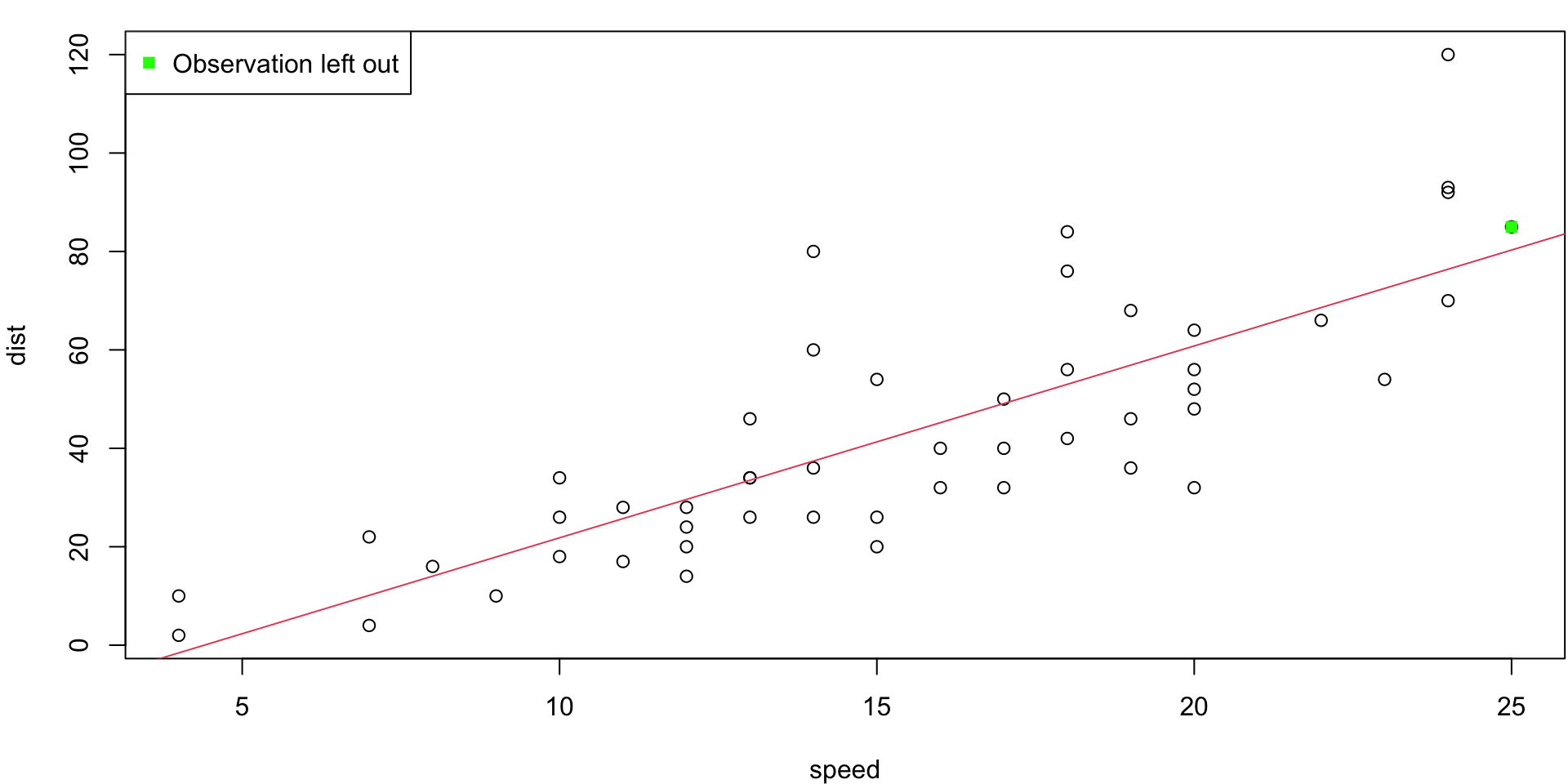
LOO regression fits
Plots the \(n\) (highly correlated) LOOCV regression fits produce a cross-validated estimates MSE = \(CV_{(n)} = 246.405416\)
5-fold CV Animation
5-fold estimates MSE as \(CV_{(5)} = 254.0391118\)
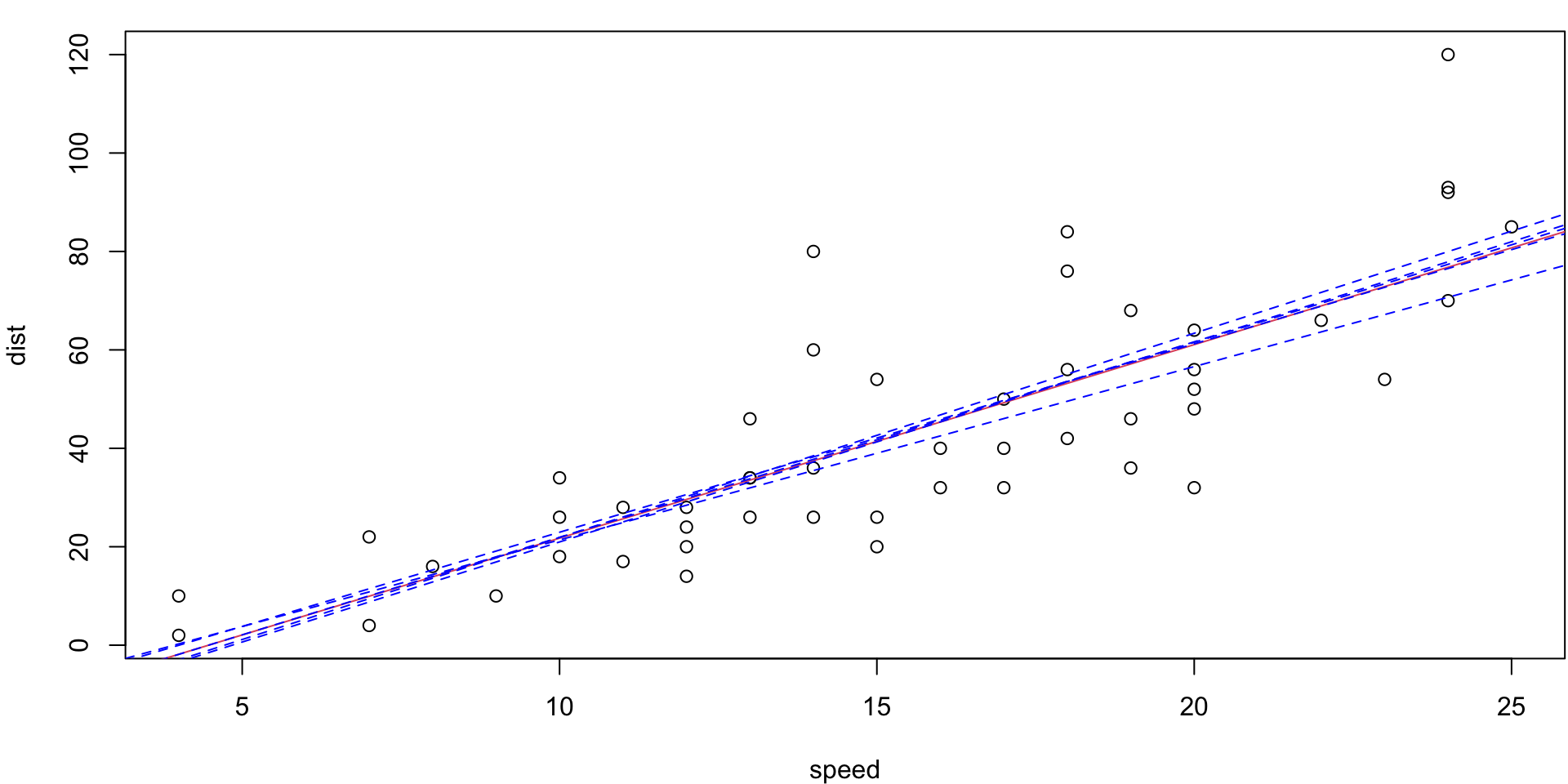
10-fold CV Animation
10-fold estimates MSE as \(CV_{(10)} = 243.7798735\)
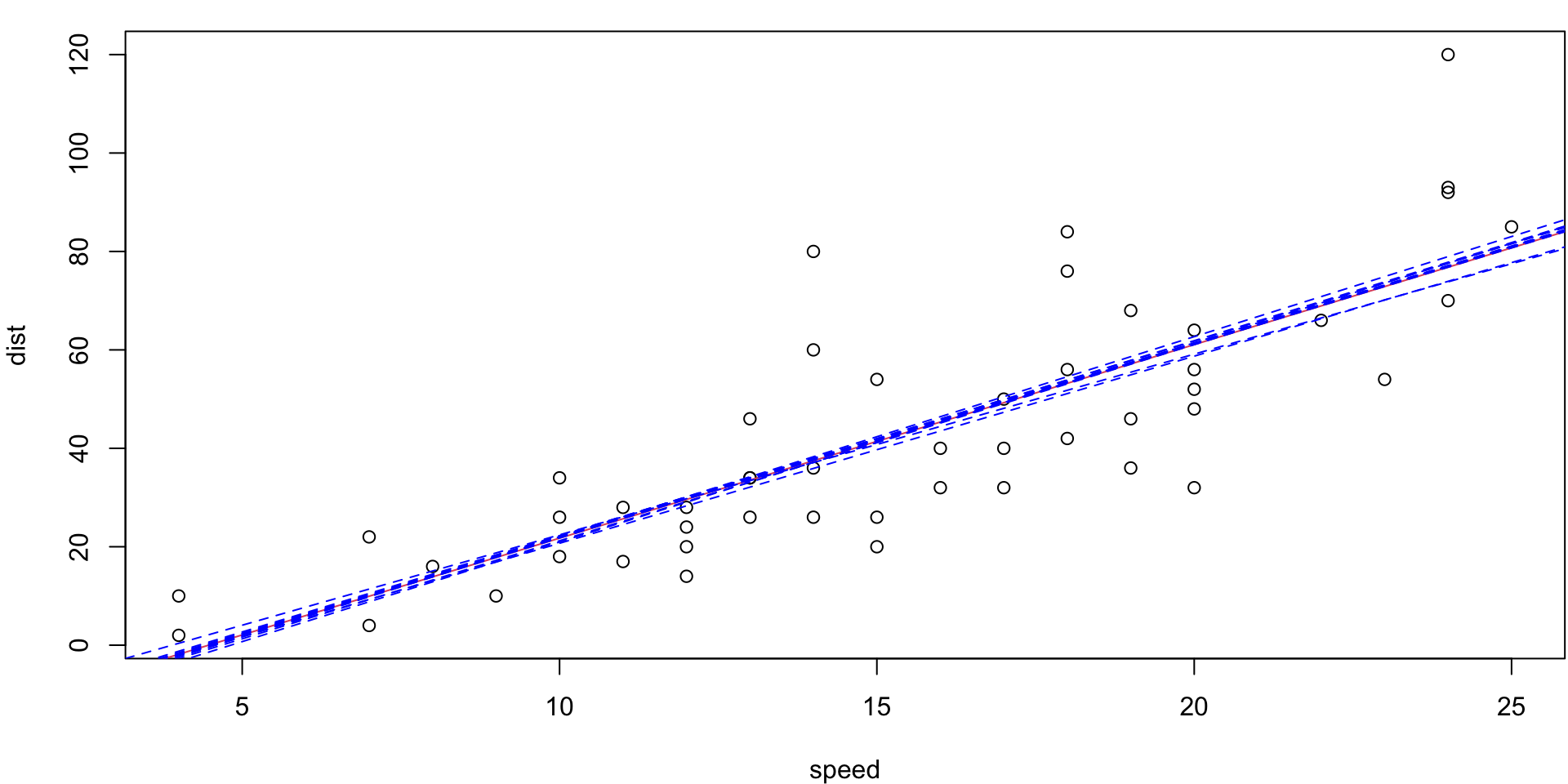
Summary
| \(k\) | \(CV_{(k)}\) |
|---|---|
| 5 | 254.04 |
| 10 | 243.78 |
| \(n\) (LOOCV) | 246.41 |

Wine example
We now consider the
winedata set from the pgmm package27 measurements on 178 samples of red wine.
Samples originate from the same region of Italy (Piedmont), but are of different varietals (Barolo, Barbera, Grignolino).
We can do KNN classification, using LOOCV1 to choose
k, the number of neighbours…
Best k
In this case the minimum is at k = 8

Wine Example
We can provide a cross-validated classification table,
Predicted
|
|||
|---|---|---|---|
| 1 | 2 | 3 | |
| Barolo | 52 | 3 | 2 |
| Grignolino | 2 | 59 | 11 |
| Barbera | 5 | 9 | 35 |
or LOOCV Error …
\[ \begin{align} CV_{(n)} &= \frac{1}{n} \sum_i^n \text{Err}_i\\ & = \frac{1}{n} \sum_i^n I(y_i \neq \hat y_i)\\ & = \frac{32}{178} = 0.18 \end{align} \]
… or cross-validated versions of any of our other classification performance indices exist!
Standard Errors
More generally: \(CV_K = \sum_{k=1}^K \frac{n_k}{n} \text{Err}_k\)
In addition to computing \(CV_K\) estimate of the error rate, we can also estimate standard deviation of \(CV_K\).
The estimated standard deviation of \(CV_K\) is given by:
\[\begin{equation} \hat{\text{SE}}(CV_K) = \sqrt{ \sum_{k=1}^{K} \left(\text{Err}_k - \overline{\text{Err}_k}\right)^2/ (K-1)} \end{equation}\]
Final Remark
- Now we have \(n\) different fits of the model, which model should we report?
None of them
While CV is used to help select a model, the actual reported model would be the one run with all the data.
That is, we would need to run
knn()withk = 8on the full data set with no observations removed.
Comments on k-Fold CV
As mentioned earlier, \(k\)-fold CV is more general than LOOCV (with the added benefit of less variance)
While \(k\) can be anything from 1 to \(n\), typically we use 5- or 10-fold CV.
While we try to subdivide the data into equally-sized non-overlapping sets, sometimes that is impossible so we approximate1
Each set (or “fold”) takes a turn as the validation set, with the remainder of the data used to train the model.
We usually shuffle the data before making the folds