Data 311: Machine Learning
Lecture 3: Assessing Models
University of British Columbia Okanagan
Recap
Supervised vs Unsupervised: categorized by the presence or absence of output (response) \(y\)
Regression vs Classification: dictated by if \(y\) is continuous (regression) vs. categorical (classification)
Goals of Inference vs Prediction
Training vs Testing
- Today we discuss the topic of model assessment to address the challenging task of model selection
Outline
In this lecture we will be covering:
- Reducible Error vs Irreducible Error
- Performance Metrics for Regression and Metrics for Classification
- Why Splitting data into a training and test set is important
- Decomposition of MSE
- Bias-Variance tradeoff
Statistical Learning Model
\[Y = f(X) + \epsilon\]
- where \(X\) are our inputs,
- \(Y\) is the numeric output (at least in this setting)
- \(\epsilon\) is the error term (independent of \(X\) and with mean 0),
- \(f\) is the systematic information \(X\) provides about \(Y\).
Goal
The primary goal in statistical learning is to estimate \(f(X)\) as accurately as possible so that the model can make reliable predictions of \(Y\) based on \(X\).
Income (Simulated) Data


Visual breakdown
The blue curve represents \(f\) the true1 underlying relationship between income (\(y\)) and years of education (\(x\)).
The black lines represent the error (\(\epsilon\)) associated with each observation.

Considering more predictors
In general, \(f\) may involve more than one input variable.

ISLR Figure 2.3 Income plotted as a function of years of education and seniority. Here \(f\) is a two-dimensional surface that must be estimated based on the observed data.
Estimates
In essence, statistical learning refers to a set of approaches for estimating \(f\).
-
Once we find \(\hat f\),our estimate for \(f\), we may obtain \(\hat Y\)s, estimates for our output \(Y\) based on
\[ \hat Y = \hat f(X) \]
- The accuracy of \(\hat Y\) depends on two things: the reducible error and the irreducible error.
Reducible Error
Reducible error refers to the part of the prediction error that can be reduced by improving the model.
It arises from inaccuracies in estimating the function \(f(X)\) with \(\hat f(X)\)
It can be reduced by using better algorithms, adjusting model complexity, gathering more data, or refining features.
A common source of reducible includes an incorrect model assumption
Irreducible Error
Irreducible error refers to the part of the prediction error that cannot be reduced or eliminated, regardless of the model or method used.
It is inherent in the variability of the response variable \(Y\) that cannot be explained by the predictors \(X\).
It represents the inherent noise in the data, measurement errors, or unobserved factors that affect the outcome.
It is our lower bound in terms of possible model accuracy
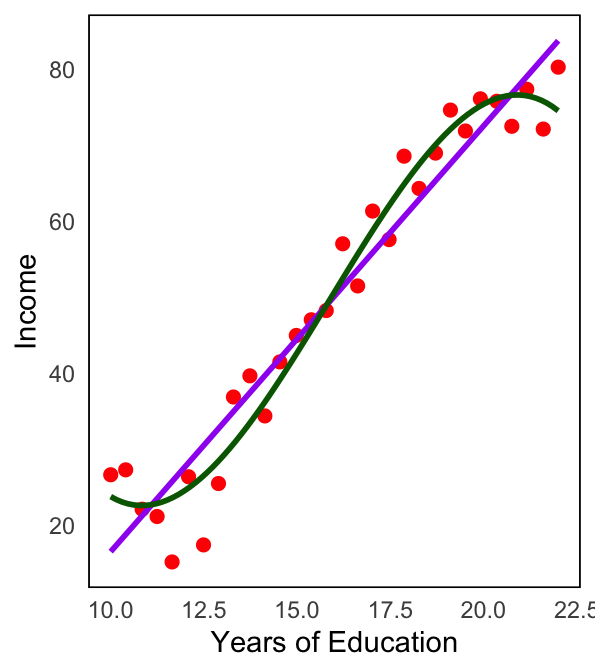
Example of Reducible error

iClicker
Which model do you think has more reducible error? A. The purple line B. The green curve
Motivation
- In practice, we won’t know \(f\), so we can’t simply measure how different \(\hat f\) is from \(f\).
- If our data is labelled, we investigate how \(\hat y\) (our predictions for some output \(y\)) compare to the observed values \(y\).
- Naturally, the closer our predicted values are to the true response value, the better.
- Our Performance Metrics will depend on whether we’re doing regression (where the output \(y\) is numeric) or classification (where the output \(y\) is categorical).
Performance Metrics
Regression
\[\begin{align} RSS &= \sum_i^n (y_i - \hat y)^2 \\ MSE &= \frac{1}{n}\sum_i^n (y_i - \hat y)^2 \\ RMSE &= \sqrt{\frac{1}{n}\sum_i^n (y_i - \hat y)^2} \end{align}\]
Classification
- Misclassification Rate
- Accuracy
- Precision
- Recall1
- F1-score
- and others …
Advertising Dataset
The Advertising dataset from the ISLR textbook which consists of the sales of a particular product across 200 different markets, along with advertising budgets for the product in different media: TV, radio, and newspaper.
market TV radio newspaper sales
1 1 230.1 37.8 69.2 22.1
2 2 44.5 39.3 45.1 10.4
3 3 17.2 45.9 69.3 9.3
4 4 151.5 41.3 58.5 18.5
5 5 180.8 10.8 58.4 12.9
6 6 8.7 48.9 75.0 7.2Suppose we wish to investigate the association between advertising and sales of a particular product …
Code
# reduce some white space in the top & right margin
par(mar=c(5.1, 4.1, 0.1, 0.1))
# Set up the plotting area for 3 plots in one row
par(mfrow = c(1, 3)) # 1 row, 3 columns of plots
plot(Advertising$TV, Advertising$sales,
xlab = "TV", ylab = "Sales")
# makes the columns available as variables
attach(Advertising)
plot(radio, sales)
plot(newspaper, sales)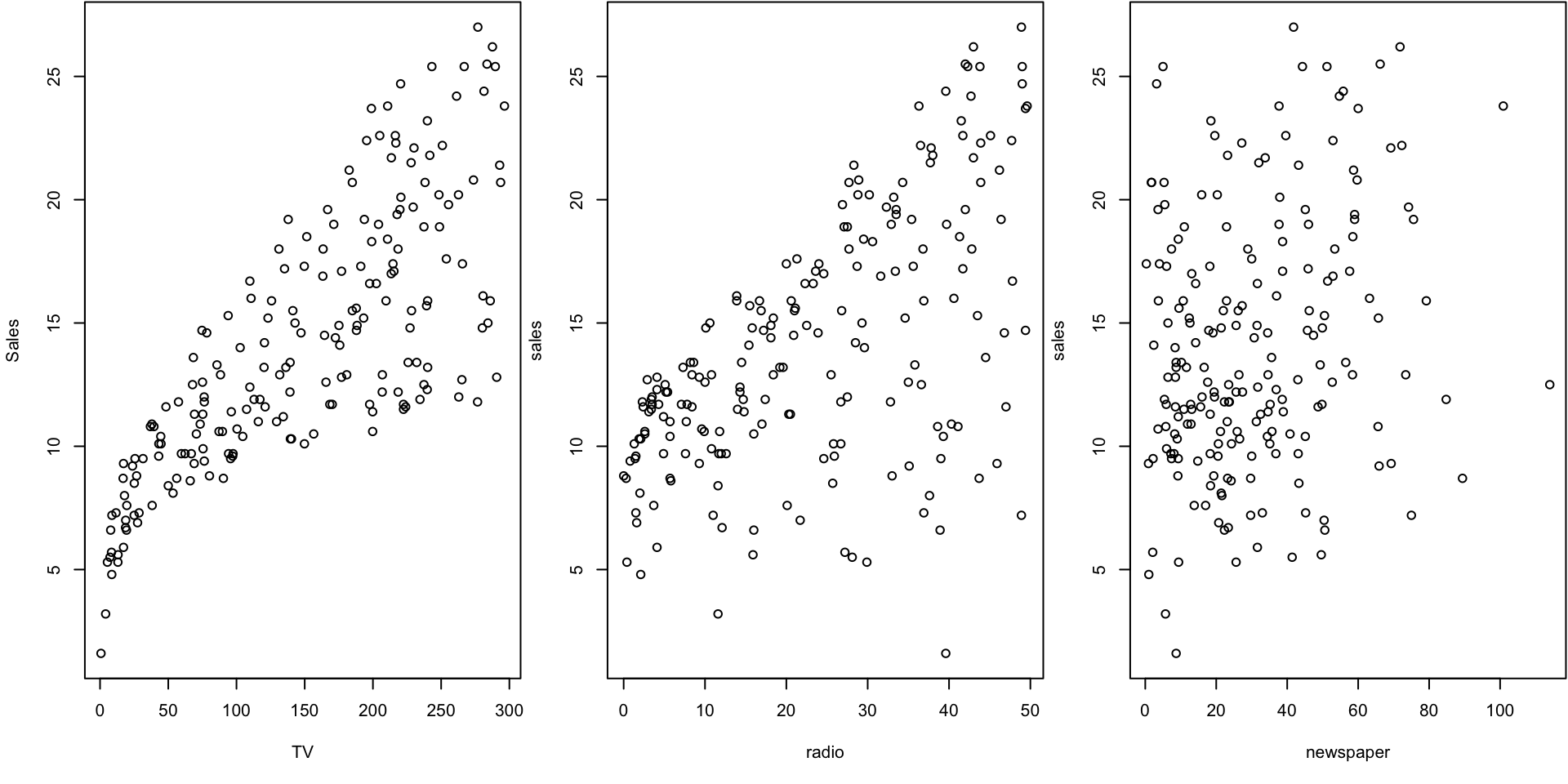
The plot displays sales, in thousands of units, as a function of TV, radio, and newspaper budgets, in thousands of dollars, for 200 different markets.
Why Estimate \(f\)?
While our performance metrics will help us choose between models, we should also keep in mind the two main reasons that we may wish to estimating \(f\):
Prediction: Forecasting future outcomes based on inputs.
Inference: Understand the relationship between variables.
Goal Prediction: In the Advertising dataset, we might want to focus on predicting the sales of product based on a set ad budget.
Goal Inference: Alternatively, we might want to understand how advertising expenditure in each medium influences sales to better allocate our spending.
Model Training Process

Metrics for Regression
Regression Problem
When the response variable is numeric, we fall into the category of regression (the topic for the next three lectures)
The most commonly-used metric for assessing performance is the mean squared error (or MSE)
In words, the MSE represents the average squared difference of a prediction \(\hat y = \hat f(x)\) from its true value \(y\).
Note that the MSE is quite sensitive to outliers.1
MSE vs RSS
\[ \text{MSE} = \frac{1}{n} \sum_{i=1}^n (y_i-\hat y_i)^2 \]
where \(\hat f(x_i) = \hat y_i\) is the prediction for the \(i\)th input \(x_i\), and \(y_i\) is the response actually observed (ie “truth”).
\[ RSS = \sum_{i=1}^n (y_i - \hat y_i)^2 \]
The MSE is closely related to the Residual Sum of Squares (or RSS) commonly in linear regression.
MSE vs RMSE
\[ \text{RMSE} = \sqrt{\text{MSE}} = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i-\hat y_i)^2} \]
- RMSE (Root Mean Squared Error) is the square root of MSE; it expresses the error in the same units as the target variable.
- This makes RMSE easier to interpret and understand compared to MSE, which is in squared units.
Metrics for Classification
Confusion matrix
When \(y\) is categorical we fall in the classification setting.
When summarizing our predictions we often look at a confusion matrix.
| Predicted Yes (+) | Predicted No (-) | |
|---|---|---|
| Actual Yes (+) | \(a\) = True Positive | \(b\) = False Negative |
| Actual No (-) | \(c\) = False Positive | \(d\) = True Negative |
Misclassification Rate
| Predicted Yes (+) | Predicted No(-) | |
|---|---|---|
| Actual Yes (+) | \(a\) = True Positive | \(b\) = False Negative |
| Actual No (-) | \(c\) = False Positive | \(d\) = True Negative |
\[\begin{align} \text{Misclassification Rate} &= \frac{b+c}{a + b + c+d} = \frac{b+c}{n} \\[0.5cm] &= \frac{\text{incorrect predictions}}{\text{total predictions}} \end{align}\]
Accuracy
| Predicted Yes (+) | Predicted No(-) | |
|---|---|---|
| Actual Yes (+) | \(a\) = True Positive | \(b\) = False Negative |
| Actual No (-) | \(c\) = False Positive | \(d\) = True Negative |
\[\begin{align} \text{Accuracy} &= \frac{a+d}{a + b + c+d} = \frac{a+d}{n} \\[0.5cm] &= \frac{\text{correct predictions}}{\text{total predictions}} \end{align}\]
Precision
| Predicted Yes (+) | Predicted No(-) | |
|---|---|---|
| Actual Yes (+) | \(a\) = True Positive | \(b\) = False Negative |
| Actual No (-) | \(c\) = False Positive | \(d\) = True Negative |
\[\begin{align} \text{Precision} &= \frac{a}{a + c} = \frac{\text{true positives}}{\text{predicted positives}} \end{align}\]
In other words, precision is the proportion of predicted “Yes”s, that are actually “Yes”
Recall (TP Rate/sensitivity)
| Predicted Yes (+) | Predicted No(-) | |
|---|---|---|
| Actual Yes (+) | \(a\) = True Positive | \(b\) = False Negative |
| Actual No (-) | \(c\) = False Positive | \(d\) = True Negative |
\[\begin{align} \text{Recall} &= \frac{a}{a + b} = \frac{\text{true positives}}{\text{actual positives}} \end{align}\]
In other words, recall (AKA sensitivity or true positive rate) is the proportion of actual “Yes”s that were predicted “Yes”.
Specificity (TN rate)
| Predicted Yes (+) | Predicted No(-) | |
|---|---|---|
| Actual Yes (+) | \(a\) = True Positive | \(b\) = False Negative |
| Actual No (-) | \(c\) = False Positive | \(d\) = True Negative |
\[\begin{align} \text{Precision} &= \frac{d}{c + d} = \frac{\text{true negatives}}{\text{actual negatives}} \end{align}\]
In other words, specificity (AKA true negative rate) is the proportion of actual “No”s that were predicted “No”
F1
A popular secondary measure is the F1 score. It is the harmonic mean1 between Precision and Recall.
\[ \text{F1} = \dfrac{2 \times \text{Precision} \times \text{Recall}} {\text{Precision} + \text{Recall}} \]
Lots of work has shown that F1 is more reliable than mis/classification rates for summarizing performance on unbalanced data sets.
MSE Visualized
Given some data: \((X, Y)\)

Fit a model \(\hat f\) (plotted in orange)
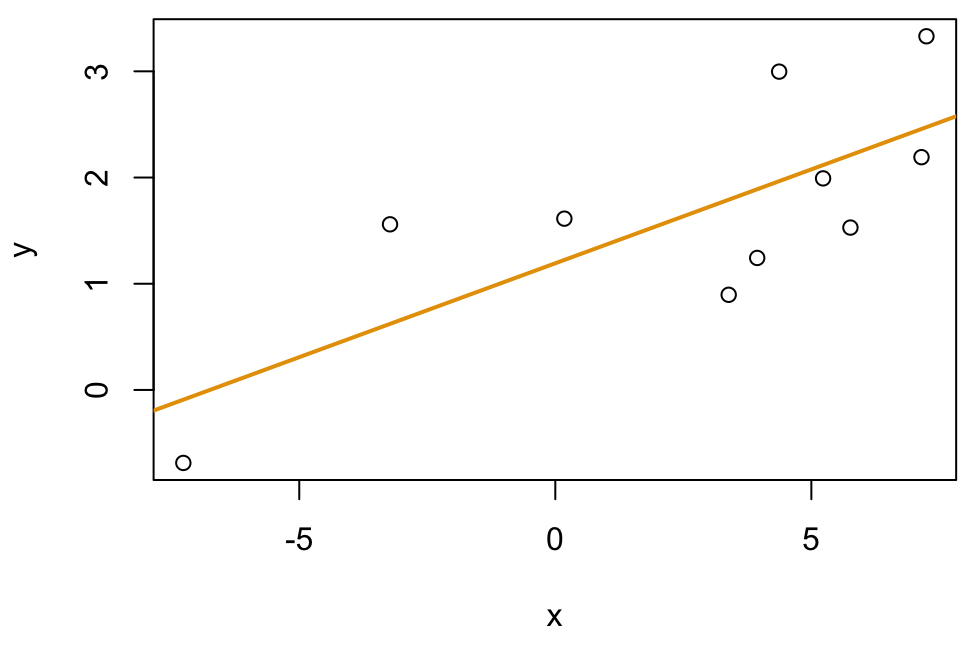
For each \(x_i\) we have a true value \(y_i\), …
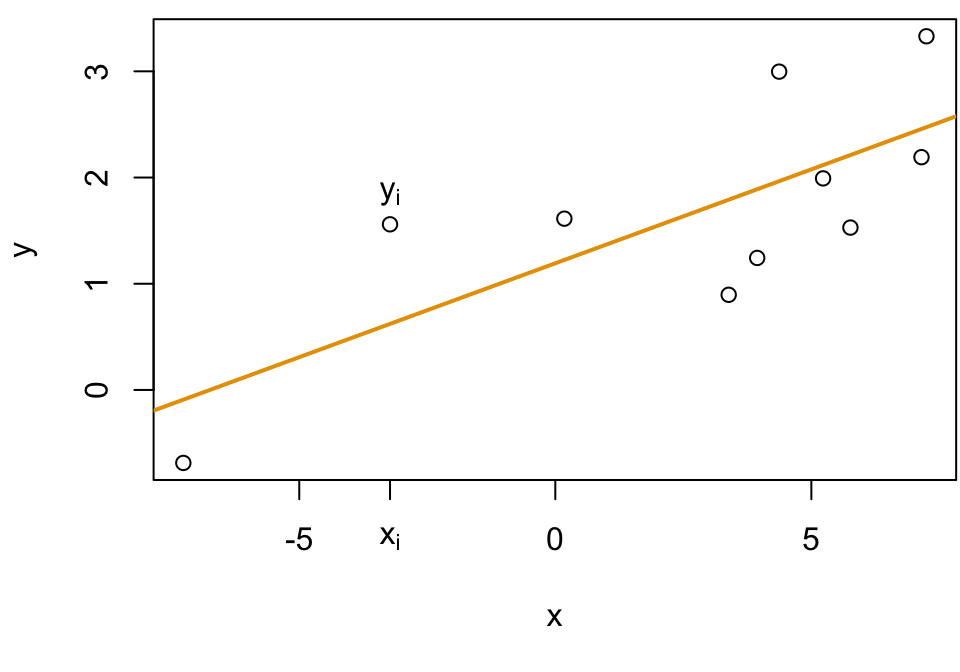
… and predicted value \(\hat f(x_i) = \hat y_i\)
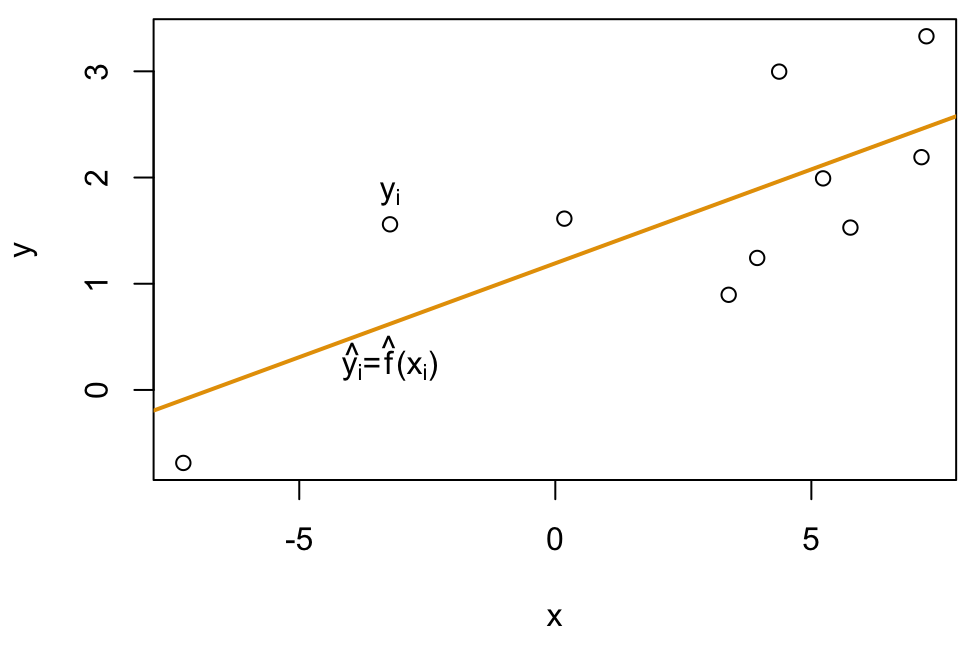
We average the squared differences to get MSE
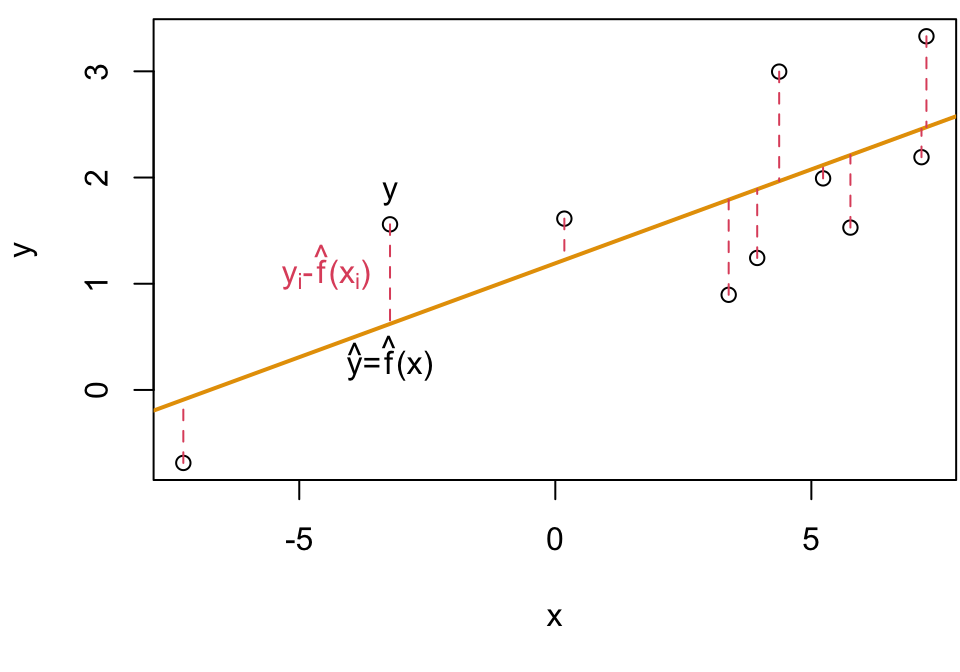
Properties of MSE
\[MSE = \frac{1}{n} \sum_{i=1}^n (y_i-\hat f(x_i))^2 \]
Notice that this has some desirable properties:
MSE is small when predicted values , \(\hat y_i - \hat f(x_i)\), are close to the true response, \(y\)
MSE is large when predicted values, \(\hat y_i - \hat f(x_i)\), are far from the true response, \(y\)
Discussion Question
Question: Would this be a good model?

Splitting

Notation
We denote the training set, i.e. the collection of observations we use to fit our model by:
\[\textbf{X}_{Tr} = \{(x_1, y_1),(x_2, y_2),...,(x_n, y_n)\} = \{x_i, y_i\}_{1}^n\]
We will denote the testing set, i.e. the collection of observations that we keep separate from the fitting process and reserve for assessing the model by:
\[\textbf{X}_{Te} = \{(x_{n+1}, y_{n+1}),...,(x_{n+m}, y_{n+m})\} = \{x_i, y_i\}_{1}^m\]
Model Fitting
We might find our \(\hat f\) based on training data \(\textbf{X}_{Tr}\) and see how close \(\hat f(x_{n+1},...,x_{n+m})\) predicts \((y_{n+1},...y_{n+m})\)
Recall that \(\textbf{X}_{Te}\) is not used to train the statistical learning method and has never been “seen” by the algorithm.


Testing vs. Training MSE
When MSE is calculated using \(\textbf{X}_{Tr}\) we call it the training MSE
\[MSE_{Tr} = \frac{1}{n} \sum_{i=1}^n (y_i-\hat f(x_i))^2\] When MSE is calculated using \(\textbf{X}_{Te}\) we call it the test MSE:
\[MSE_{Te} = \frac{1}{m} \sum_{i=1}^m (y_i-\hat f(x_i))^2\]
MSE train = average squared differences using training data

MSE test = average squared differences using the test data
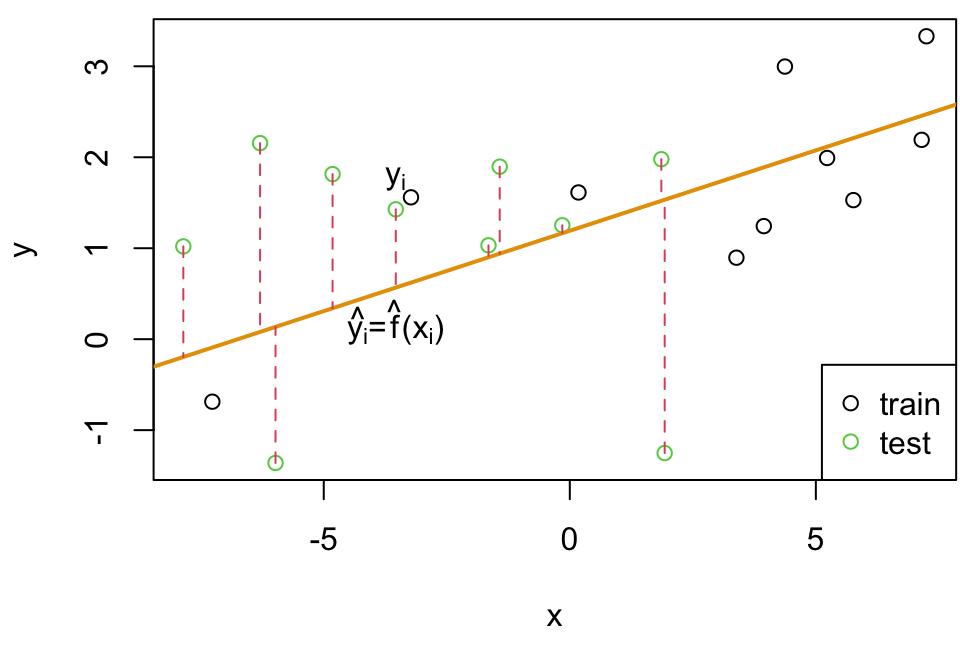
iClicker
iClicker
Which of the following statements is generally true about MSE (Mean Squared Error) on the training and testing sets?
MSE on the training set tends to be smaller than on the testing set.
MSE on the testing set tends to be smaller than on the training set.
MSE on both sets should be equal for a good model.
MSE on the training set tends to be larger than on the testing set.
Correct answer: A. MSE on the testing set is typically larger than MSE on the training set because the model is optimized and fitted to the training data, often leading to better performance on that data compared to unseen testing data.
Goal
- Plainly speaking, we do not really care how well the method works on the training data.
- We are interested in the accuracy of predictions to data it’s never seen before, e.g. new patients, future stock prices, …
MSE testing vs MSE training
\(\text{MSE}_{Te}\) is a metric of how well \(\hat f\) generalizes to unseen data, thus, we want this (rather than \(\text{MSE}_{Tr}\)) to be as low as possible.
Math
Suppose, for notational convenience, we have a training set \(X_{Tr} = S\) that was used to fit our model \(\hat f_S\). Given a test set \(X_{Te} = (X, Y)\), we can write our expected prediction error as:
\[\begin{align*} &= E[(y - \hat y)^2]\\ &= E[(y - \hat f_S(x))^2]\\ &= E[(f(x) + \epsilon - \hat f_S(x))^2]\\ &= E[\left((f(x) - \hat f_S(x)) + \epsilon \right)^2]\\ &= E[(f(x) - \hat f(x))^2 + 2(f(x) - \hat f(x))\epsilon + \epsilon^2]\\ &= E[(f(x) - \hat f(x))^2] + 2E[(f(x) - \hat f(x))\epsilon] + E[\epsilon^2]\\ \end{align*}\]
Since \(\epsilon\) and \(\hat f(x)\) are independent; recall \(E[XY] = E[X]\cdot E[Y]\) when \(X\perp Y\)
\[\begin{align*} &= E[(f(x) - \hat f(x))^2] + 2E[(f(x) - \hat f(x))]E[\epsilon] + E[\epsilon^2]\\ \end{align*}\]
Recall an assumption of Statistical learning models: \(E[\epsilon] =0\)
\[\begin{align*} &= E[(f(x) - \hat f(x))^2] + E[\epsilon^2]\\ \end{align*}\]
Since \(\text{Var}(\epsilon) = E[\epsilon^2] - (E[\epsilon])^2 = E[\epsilon^2] \text{ (since } E[\epsilon] = 0)\)
\[\begin{align*} &= E[\underbrace{(f(x) - \hat f_S(x))^2}_{\text{reducible error}}] + \underbrace{\text{Var}[\epsilon]}_{\text{irreducible error}}\\ \end{align*}\]
Math (cont’d)
Reducible error can be further decomposed into error due to squared bias and variance.
\[\begin{align*} &= \mathbb{E}\left[\text{reducible error}\right]\\ &=\mathbb{E}\left[ (f(x) - \hat f_S(x))^2 \right]\\ &= \underbrace{ (f(x) - \mathbb{E}[\hat f_S(x)])^2 }_{\text{Bias}^2(\hat f(x))} + \underbrace{ \mathbb{E}\left[ (\hat f_S(x) - \mathbb{E}[\hat f_S(x)]^2) \right]}_{\text{Var}(\hat f(x))} \end{align*}\]
Decomposition of MSE
All together we have the expected test MSE at a new point \(x\).
\[\begin{align*}
&=\text{E}_{Y|x, S}\left[(y - \hat f (x))^2\right] \\
&=\underbrace{\text{Bias}^2(\hat f(x)) + \text{Var}(\hat f(x))}_{\text{reducible error}} + \underbrace{\text{Var}(\epsilon)}_{\text{irreducible error}}
\end{align*}\] It’s the average \(MSE_{Te}\) we’d get if we repeatedly estimated \(f\) using a large number of training sets, and tested at each at \(x\)
Types of Error revisted
-
The variance of error term \(\epsilon\) is our irreducible error.
- a measure of the amount of noise in our data.
- even if we estimate \(f\) perfectly, our data will always have some noise that can not be reduced.
This shows us that the reducible error (as defined earlier) is composed of bias and variance components.
Our goal can be rephrased as minimizing the reducible error by decreasing the bias and variance as much as possible
Problem
Problem: as we tend to decrease the bias, we tend to increase the variance and vice versa.
There is an inherent trade-off between bias and variance is known as the Bias Variance Tradeoff
Understanding these components (bias/variance a model) will help us in selecting and tuning models to improve their performance on new, unseen data.
Bias-Variance
Bias
Bias (of a model) refers to the error that is introduced by approximating a real-life problem, which may be extremely complicated, by a much simpler model.
- High bias can cause an algorithm to miss the relevant relations between features and target outputs (underfitting)


Variance
Variance refers to the amount by which \(\hat f\) would change if we estimated it using a different training data set.
- High variance may result from an algorithm modeling the random noise in the training data (overfitting).


Target Visualizations

Inspired by Essays by Scott Fortmann-Roe
Target Explained (Bias)

- Low Bias (first row) models approximate the real-life problem well; that is \(\hat f\) will be centered around \(f\) (🎯)
- High Bias (second row) will systematically be “off the mark”; these tend to be models that are too simple
Impact High bias leads to underfitting, where the model performs poorly on both the training set and new, unseen data. It fails to learn the true relationships in the data adequately.
Target Explained (Variance)

Low variance (first column) indicates that \(\hat f\) would not change much even if we estimated it using a different training data set. (so the hits will all be close together)
High variance (second column) indicates that \(\hat f\) will be very sensitivity to small fluctuations in the training; tend to be models that are overly complex
Impact High variance leads to overfitting, where the model performs well on the training data but poorly on new, unseen data because it is too closely fitted to the quirks of the training set.
Simulations
Let’s simulate a training set of size \(n = 100\) by uniformly generating \(X\) values between 0 and \(2\pi\), and generate \(Y\) values according to this formula (\(f(x) = \sin(x)\)): \[\begin{align*} Y &= \text{sin}(X) + \epsilon \end{align*}\] where \(\epsilon \sim \text{Normal}(\mu =0, \sigma = 1)\).
Training set 1
Training set #1: This is one example of a potential training set

Training set 2
Training set #2: Here’s another…

Generative Model
Since we know \(f\) we can plot as well

Low Variance High Bias

Training set 1
Let’s start by fitting a simple linear regression (SLR) model to training set #1. The resulting fitted line \(\hat f\) is plotted below

Training set 2
Fitting a SLR to training set #2 will produce this (slightly different) fitted line \(\hat f\)

10 training sets
The fitted line for 10 different fits using 10 different training sets.
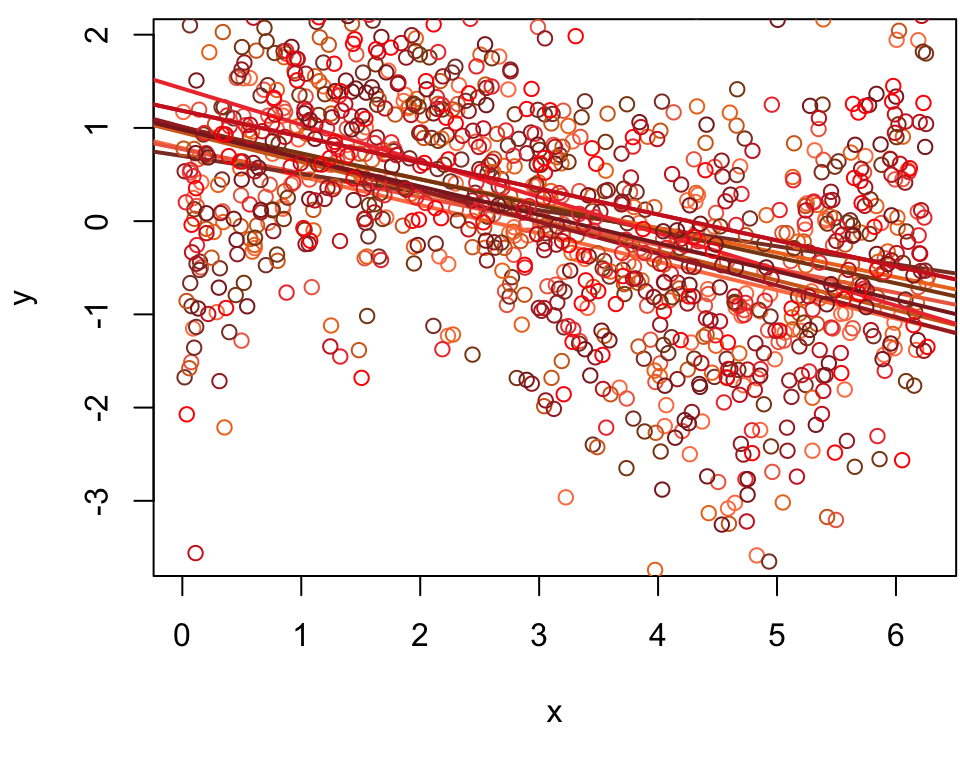
Low Variance
If we do this repeatedly on different training sets simulated from the same model described on this slide, you will notice that we don’t get very much variation in our fitted model.
This model is therefore said to have low variance.
That is to say, it is not sensitivity to small fluctuations in the training set.
High Bias
High bias refers to a situation where a model makes strong simplifying assumptions about the data, resulting in systematic errors in its predictions.
- this straight line is not flexible enough to capture the curved relationship between these two variables
Underfitting is a consequence of high bias. It refers to the poor performance of a model on both the training and test data due to its inability to capture the data’s underlying patterns.
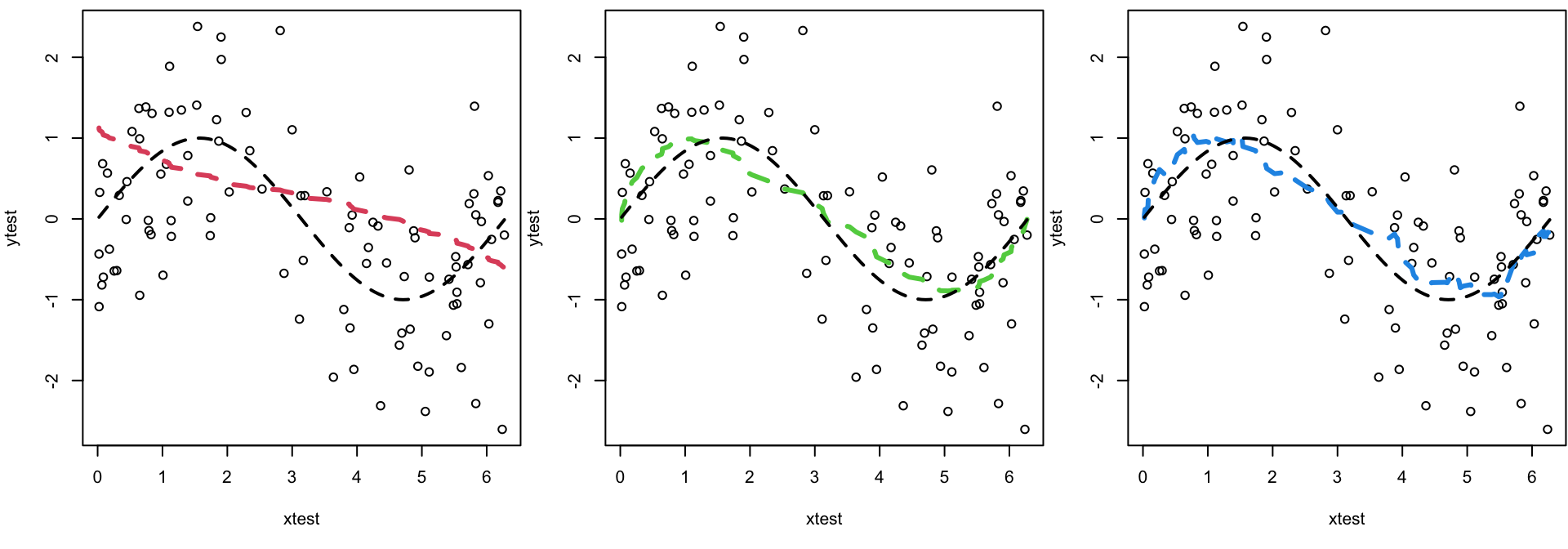
Low Bias High Variance

Green Model
To demonstrate this concept we’ll use the local polynomial model (using the
loessfunction in R).We will call this the “green model”
Don’t worry if you don’t know what this model is. We are unlikely to cover these in this course — just consider it a relatively flexible model.
Training set 1
Fitting a highly flexible loess model to training set #1 will produce this fitted curve \(\hat f\)
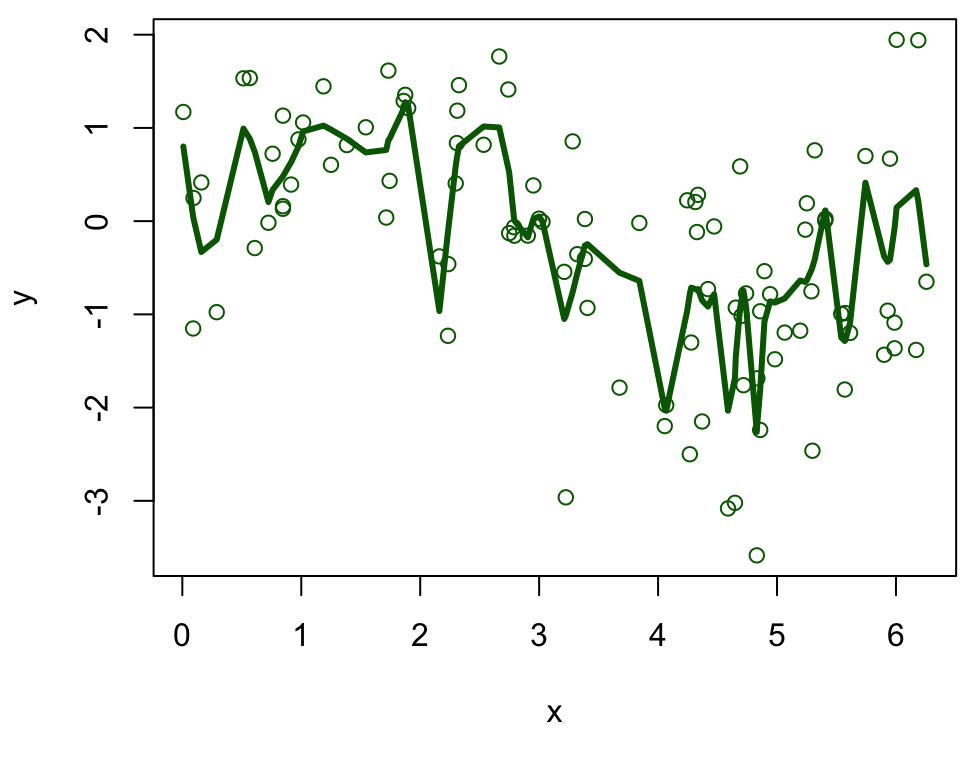
Training set 2
Fitting a highly flexible loess model to training set #2 will produce this (very different) fitted curve \(\hat f\)
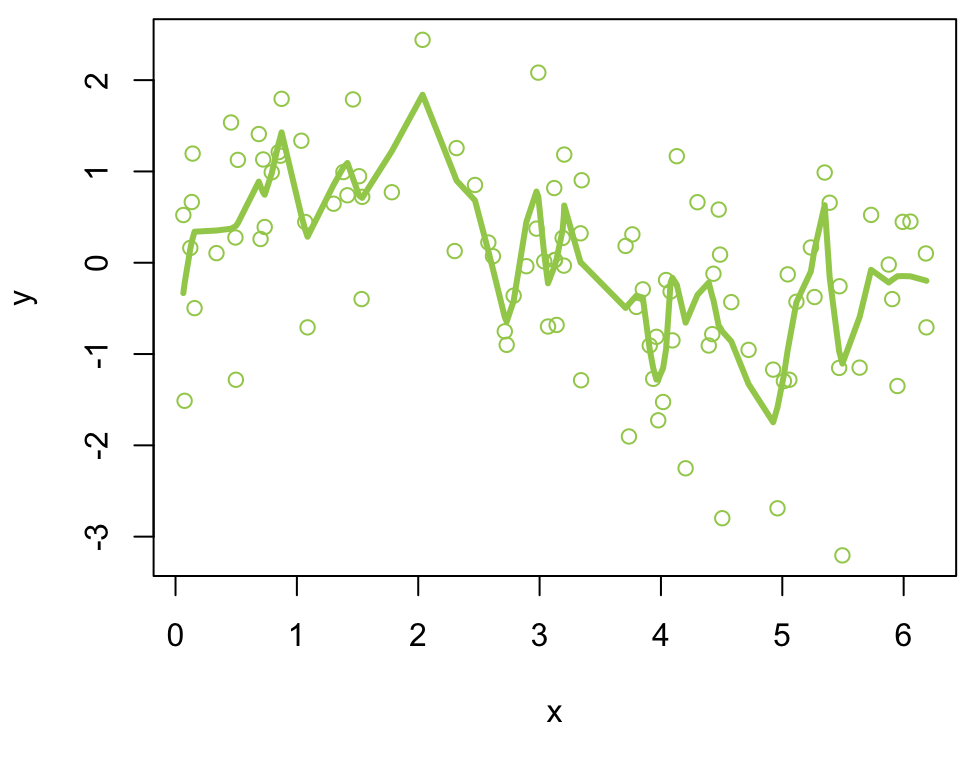
10 training sets
The fitted model for 10 different fits using 10 different training sets.
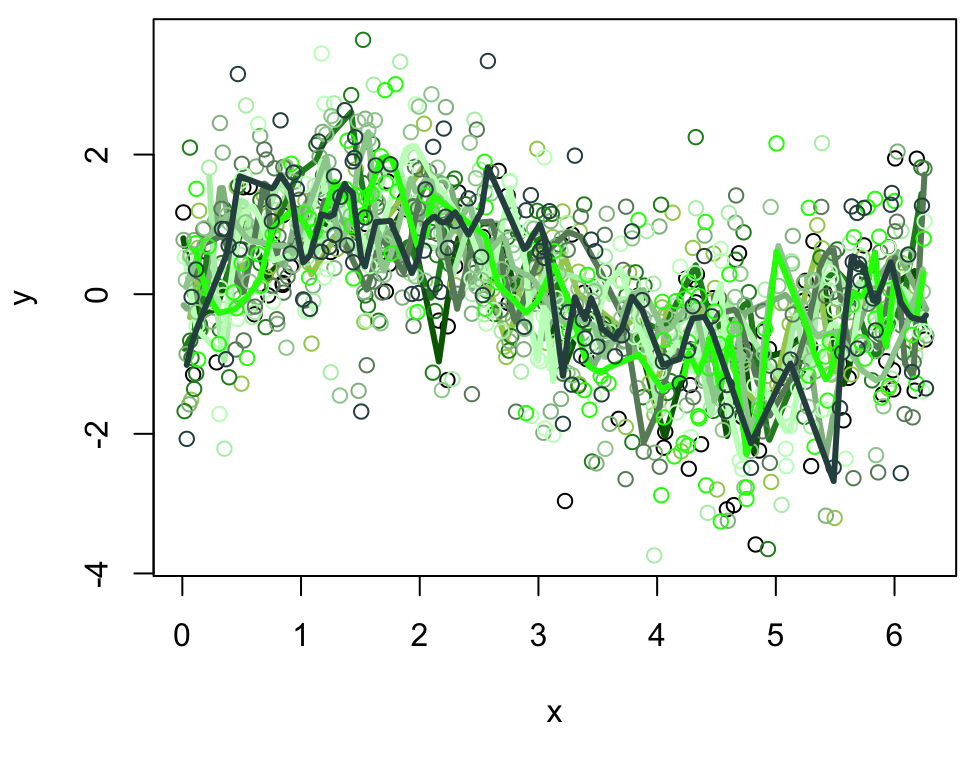
High Variance
High Variance models tend to to capture noise and random fluctuations in the training data rather than the underlying patterns.
- This “green” model has high variance since it is very sensitivity to small fluctuations in the training set and highly variable from training set to training set.
Models like these are said to be overfitting to the training data. Overfitting tends to result in very low training error and comparitively high testing error (poor generalization)
Low Bias
\[\text{Bias}^2(\hat f(x)) = (f(x) - \mathbb{E}[\hat f_S(x)])^2 \]
While small changes in training set causes the estimate \(\hat f\) to change considerably, on average, it is capturing the general sine wave nature of this data.
Thus the green model has low bias.
Even though a single fitted model corresponds too closely to the training data, on average this model is close the truth.
Low bias and Low variance

Blue Model
As before we will use the local polynomial model (using the
loessfunction in R) to fit this model.We will call this the “blue model”
We will adjust the
spanargument to decrease the level of flexibility.
Training set 1
Fitting a loess model with medium flexibility to training set #1 will produce this fitted curve \(\hat f\) plotted below
Training set 2
Fitting a loess model with medium flexibility to training set #2 will produce this (different) fitted curve \(\hat f\)

10 training sets
The fitted model for 10 different fits using 10 different training sets.

Low Variance
If we do this repeatedly on different training sets simulated from the same model described on this slide, you will notice that we don’t get very much variation in our fitted model.
This model is therefore said to have low variance
That is to say, it is not sensitivity to small fluctuations in the training set.
Low Bias
The blue model has low bias.
That is, on average the estimate is close the truth.
Unlike the green model (which also has low bias), this model is not overfitting to the data (low bias).
The blue model strikes a nice balance between low variance and low bias.
Average model across simulations
Let’s explore what the average model looks like for each of these scenarios …
Goldilocks Principle

Image adapted from MollyMooCrafts
Bias Variance Tradeoff
Since the test MSE is comprised of both bias and variance we want to try to reduce both of them.
However, as we decrease bias, we tend to increase variance and vice versa.
iClicker
iClicker
iClicker
What does high bias in a model typically lead to?
A. Overfitting
B. Underfitting
C. Good generalization
D. High variance
Correct answer: B. Underfitting
iClicker
iClicker
Which of the following best describes a high variance model?
A. The model performs well on new data.
B. The model has low flexibility.
C. The model captures noise in the training data.
D. The model makes strong assumptions about the data.
Correct answer: C. The model captures noise in the training data.
iClicker
iClicker
What is the primary goal when managing the bias-variance tradeoff?
A. To maximize bias and minimize variance.
B. To eliminate variance completely.
C. To minimize both bias and variance equally.
D. To find a balance that minimizes overall prediction error.
Correct answer: D. To find a balance that minimizes overall prediction error.
iClicker
iClicker
As model flexibility increase, the bias tends to __________________
A. decrease
B. increase
C. stay the same
D. it depends
Correct answer: A. decrease
iClicker
iClicker
As model flexibility increase, the variance tends to __________________
A. decrease
B. increase
C. stay the same
D. it depends
Correct answer: B. increase
Bias-Variance Tradeoff visualized

iClicker
iClicker
As model flexibility increase, the MSE training will tends to __________________
A. decrease
B. increase
C. stay the same
D. it depends
Correct answer: A. decrease
iClicker
iClicker
As model flexibility increase, the MSE test will tends to __________________
A. decrease
B. increase
C. stay the same
D. it depends
Correct answer: D. it depends
MSE visualized

Looking Forward
To manage the variance-bias tradeoff effectively, you can employ techniques such as cross-validation, regularization, feature selection, and ensemble methods (e.g., bagging and boosting), all of which will be discussed throughout the course.
These techniques help you find the optimal model complexity and reduce overfitting or underfitting, ultimately improving a model’s generalization performance.
ISLR Simulations
The ISLR textbook (section 2.2.2) has similar simulations that I encourage to go through on your own. You can skim through the slides here which we will summarize in class only if time permits.
Section 2.2.2
The following simulations are taken from your ISLR2 textbook.
Looking at a variety of different data we can gain some general insights on \(\text{MSE}_{Te}\) and \(\text{MSE}_{Tr}\)
Again, the particulars about the specific models (linear regression and loess smoothing splines) are not important.
What is important is it understand how the level of flexibility impact the bias and variance of the models (and therefore the MSE).
Figure 2.9 (left plot)

ISLR Figure 2.9 (left plot) Data simulated from \(f\), shown in black. Three estimates of \(f\) are shown: the linear regression line (orang ecurve), and two smoothing spline fits (blue and green curves). jump to right-hand panel

Orange curve
High bias, low variance
Low Variance the oranage fit would not have much variability from training set to training set
High Bias it systematically underestimate between 40–80 and overestimate towards the boundaries, for example.

Green curve
Low bias, high variance
As the green curve is the most flexible, it matches the training data very closely
However, it is much more wiggly than \(f\) (ie the “true” generating black curve)

Blue curve
Low bias, low variance
The blue curve strikes the balance between low variance and low bias
As one may expect, the average fitted curve is quite similar to \(f\) (ie the “true” generating black curve)
Estimated test MSE
To estimate the expected \(\text{MSE}_{Tr}\) and \(\text{MSE}_{Te}\) their values over a very large collection of data sets.
The average training MSE and testing MSE is plotted in gray and red, respectively, as a function of flexibility.
The flexibility of these models are mapped to numeric values on the \(x\)-axis (lower values indicate less flexibility).
Squares (🟧, 🟦, 🟩) indicate the MSEs associated with the corresponding orange, blue, and green models.
Figure 2.9 (right)

ILSR Figure 2.9 (right plot) Training MSE (grey curve), test MSE (red curve), and minimum possible test MSE over all methods (dashed line). Squares represent the training and test MSEs for the three fits shown in the left-hand panel.

Test MSE
The orange and green models have high \(\text{MSE}_{Te}\) but for different reasons
- orange is underfitting
- green is overfitting
Blue is close to optimal

Minimizing test MSE
The horizontal dashed line indicates \(\text{Var}(\epsilon)\), the irreducible error
This line corresponds to the lowest achievable test MSE among all possible methods.
Hence, the “blue model” is close to optimal.

Training MSE
The green curve has the lowest training MSE of all three methods, since it corresponds to the most flexible of the three curves fit in the left-hand panel

Training MSE
The orange curve has the highest training MSE of all three methods, since even on the training set, it is not flexible enough to approximate the underlying relationship

Training MSE
The blue curve obtains a similar training and testing MSE.
iClicker
iClicker
If the MSE on the training set is much lower than the MSE on the testing set, what does this indicate about the model?
A. The model is underfitting.
B. The model is overfitting.
C. The model is well-generalized.
D. The model has high bias.
Correct answer: B. The model is overfitting.
General Trends
The U-shaped test MSE is a fundamental property of statistical learning that holds regardless of the particular dataset and statistical method being used.
As model flexibility increases, the training MSE will decrease, but the test MSE may not.
When a method yields a small training MSE but a large test MSE, is is said to be overfitting the data.
We almost always expect the training MSE to be smaller than the test MSE.
The training MSE declines monotonically as flexibility increases.
Comments
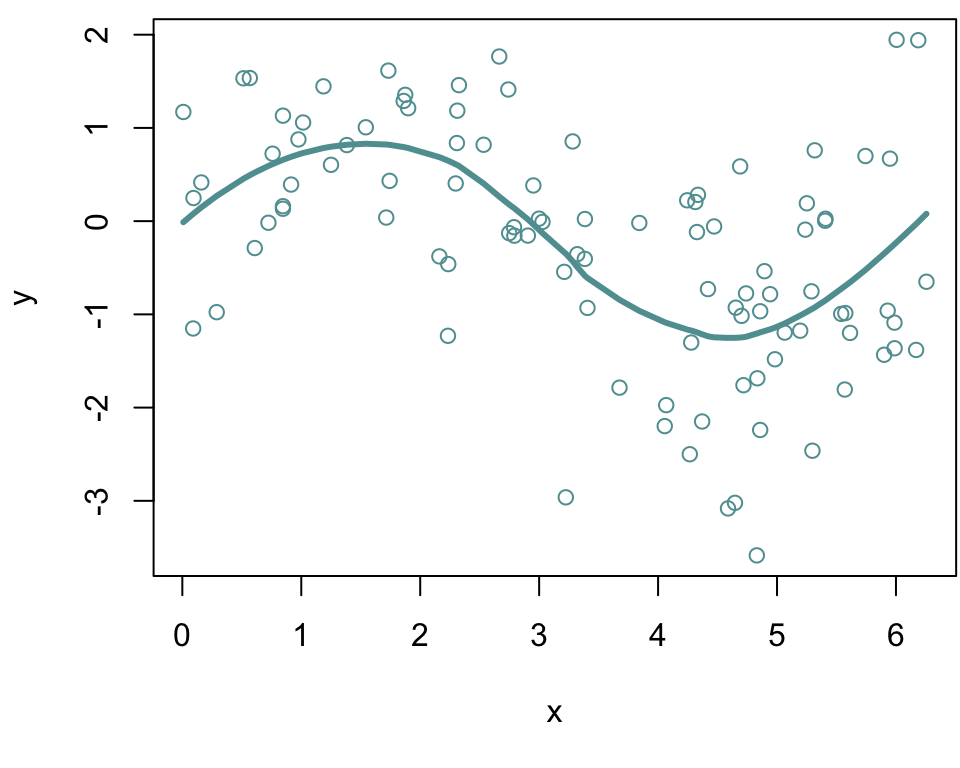
The purple model assumes a straight-line relationship between the predictor (Years of Education) and the response (Income)
However, the true relationship, as indicated by blue curve, is non-linear and follows a curved pattern.
Since the linear model (purple) does not capture the curvature it systematically1 deviates from the true relationship.
This discrepancy contributes to the reducible error since this error could be reduced by fitting a more appropriate model that accounts for the curve, such as a polynomial model (green curve).