
Data 311: Machine Learning
Lecture 9: Distance Measures
University of British Columbia Okanagan
Recap
So far we’ve been in the supervised setting where we know the “answers” for response variable \(Y\) which might be continuous (regression) or categorical (classification)
Simple methods for modeling a continuous response variable include: regression, KNN-regression
Simple methods for modeling a categorical response variable include: logistic regression, discriminant analysis, KNN-classification
Introduction
We are moving towards the realm of unsupervised learning; that is, problems for which we do not have known “answers”.
Prior to diving deep on unsupervised methods, it’s important to note that the vast majority are based on distance calculations (of some form).
Distance seems like a straightforward idea, but it is actually quite complex …

Outline
Distance Motivation
What is the distance from Trump Tower to Times Square?

What is the distance from Trump Tower to UBCO?
In this case we would need to take into account the curvature of the Earth!
Euclidean Distance
- To begin, we’ll consider that all predictors are numeric.
The Euclidean distance between observations \(x_i = (x_{i1}, x_{i2}, \dots x_{ip})\) and \(x_j = (x_{j1}, x_{j2}, \dots x_{jp})\) is calculated as \[d^{\text{EUC}}_{ij} = \sqrt{\sum_{k=1}^p (x_{ik} - x_{jk})^2}\]
- While simple, it is inappropriate in many settings.
Where Euclidean Fails 1
- Consider the following measurements on people:
- Height (in cm),
- Annual salary (in $)
- A $61 difference in annual salary would be considered a minuscule difference, whereas a 61 cm difference in height (approx 2 feet) would be substantial!
Plotted Euclidean Distance

Is it reasonable to assume A is equidistant (at equal distances) with points B and C?
Scale Matters
The scale and range of possible values matters!
If we use a distance-based method, for example KNN, then large scale variables (like salary1) will have a larger effect on the distance between the observations, than variables that are on a small scale (like height).
Hence salary will drive the KNN classification results2.
Standardized Euclidean Distance
One solution is to scale the data to have mean 0, variance 1 via \[z_{ik} = \frac{x_{ik}-\mu_k}{\sigma_k}\] Then we can define standardized pairwise distances as \[d^{\text{STA}}_{ij} = \sqrt{\sum_{k=1}^p (z_{ik} - z_{jk})^2}\]
How it might look after scaling

After scaling those data you might have something more along the lines of this, were C and A are much closer together than A and B
Manhattan Distance
Manhattan distance1 measures pairwise distance as though one could only travel along the axes \[d^{\text{MAN}}_{ij} = \sum_{k=1}^p |x_{ik} - x_{jk}|\]
Similarly, one might want to consider the standardized form \[d^{\text{MANs}}_{ij} = \sum_{k=1}^p |z_{ik} - z_{jk}|\]
Manhattan Visualization
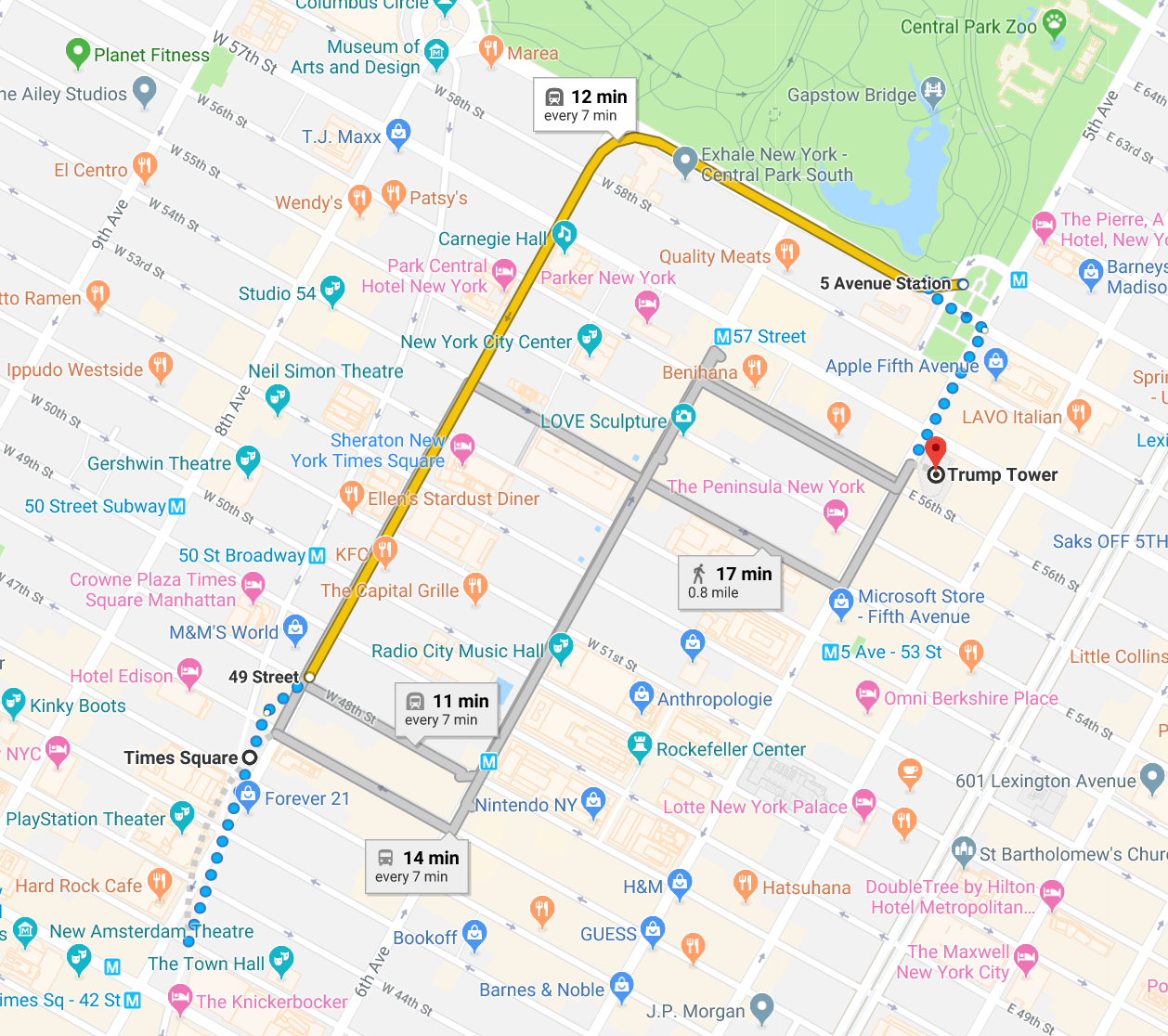
Image sources: Google Maps 2021
Manhattan Visualization 2

The red, yellow, and blue paths all have the same Manhattan distance of 12.
The green line has Euclidean distance of \(6 \sqrt {2} \approx 8.49\) and is the unique shortest path.
Euclidean Visualization

Where Euclidean Fails 2
Euclidean distance can lead to some misleading results when the variables are highly correlated.
Let’s consider data simulated from the bivariate normal distribution having
Simulation

Which point would you consider more unusual? A or B?
Euclidean Distance for Simulation

- The euclidean distance between A and \(\mu\) is 5
Euclidean Distance for Simulation

The euclidean distance between A and \(\mu\) is 5
The euclidean distance between B and \(\mu\) is 8.16
B is father in terms of Euclidean distance from the center of this distribution, but it is “closer” to the blob of points than A.
Mahalanobis Distance
Mahalanobis distance takes into account the covariance structure of the data.
It is easiest defined in matrix form \[d^{\text{MAH}}_{ij} = \sqrt{(x_i - x_j)^T \boldsymbol{\Sigma}^{-1} (x_i - x_j)}\] where \(^T\) represents the transpose of a matrix and \(^{-1}\) denotes the inverse of matrix.
Mahalanobis Distance for Simulation

- The Mahalanobis distance from point \(\mu\) to A is 64.83
Mahalanobis Distance for Simulation

The Mahalanobis distance from point \(\mu\) to A is 64.83
The Mahalanobis distance from point \(\mu\) to B is 4.57
B is closer to \(\mu\) in terms of Mahalanobis distance than A is, despite A being closer to \(\mu\) in terms of Euclidean distance.
Computing Distances in R:
Euclidean
[1] 5
[1] 8.163333
A B
B 10.002000
mu 5.000000 8.163333Mahalanobis
When to Standardize?
- This brings us to an important question…when should we use a standardized measure, and when should we not?
- It is often a good idea, and generally necessary if measurements are on vastly different units.
- Unless you have a good reason to believe that higher variance measures should be weighted heavier, then you probably want to standardize in some form.
From Numeric to Mixed
What if some/all the predictors are not numeric?
We can consider several methods for calculating distances based on matching.
For binary data case, we can get a “match” either with a 1-1 agreement or 0-0.
Matching Binary Distance
- We can actually define another matching method that is equivalent to Manhattan/city-block,
\[d^{\text{MAT}}_{ij} = \text{\# of variables with opposite value}\]
This is simple sum of disagreements is the unstandardized version of the M-coefficient.
Let’s see an example,…
President Example
Let’s look at some binary variables for US presidents:
-
Democratlogical indicating if they are a democrat -
Govenorlogical indicating if they were they formerly a governor 1 = yes -
VPlogical indicating if they were formerly a vice president -
2nd Termlogical indicating if they serve a second term -
From Iowalogical indicating if they are originally from Iowa
Matching Binary Distance
| Democrat | Governor | VP | 2nd Term | From Iowa | |
|---|---|---|---|---|---|
| GWBush | 0 | 1 | 0 | 1 | 0 |
| Obama | 1 | 0 | 0 | 1 | 0 |
| Trump | 0 | 0 | 0 | 0 | 0 |
The Manhattan distance between GWBush vs Obama: \[|0-1|+|1-0|+|0-0|+|1-1|+|0-0| = 2\] This is equivalent to \(d^{\text{MAT}}_{12}\) (as they do not match in two variables: Democrat and Governor).
M-coefficient
The M-coefficient (or matching coefficient) is simply the proportion of variables in disagreement in two objects over the total number of variable comparisons, p.
So in our presidents example the matchin distance can be converted to a proportion by calculating
\[ \begin{equation} d_{12}^{MATp} = \frac{2}{5} = 0.4 \end{equation} \]
Calculate M-coefficient
| Democrat | Governor | VP | 2nd Term | From Iowa | |
|---|---|---|---|---|---|
| GWBush | 0 | 1 | 0 | 1 | 0 |
| Obama | 1 | 0 | 0 | 1 | 0 |
| Trump | 0 | 0 | 0 | 0 | 0 |
Calculating the simple matching M-coefficient1 \[d^{\text{M-coef}}_{12} = \frac{2}{5} = 0.4\]
Question
| Democrat | Governor | VP | 2nd Term | From Iowa | |
|---|---|---|---|---|---|
| GWBush | 0 | 1 | 0 | 1 | 0 |
| Obama | 1 | 0 | 0 | 1 | 0 |
| Trump | 0 | 0 | 0 | 0 | 0 |
Should a 0-0 match in
From Iowareally map to a binary distance of 0?Since a 0-0 “match” does not imply that they are from similar places in the US, I would argue not.
Asymmetric Binary Distance
For reasons discussed on the previous slide, it makes sense to toss out those 0-0 matches.
In this case, what we would be considering is asymmetric binary distance
\[d^{\text{ASY}}_{ij} = \frac{\text{\# of 0-1 or 1-0 pairs}}{\text{\# of 0-1, 1-0, or 1-1 pairs}}\]
Calculate Asymmetric Distance
| Democrat | Governor | VP | 2nd Term | From Iowa | |
|---|---|---|---|---|---|
| GWBush | 0 | 1 | 0 | 1 | 0 |
| Obama | 1 | 0 | 0 | 1 | 0 |
| Trump | 0 | 0 | 0 | 0 | 0 |
The asymmetric binary distance between Bush and Obama:
\[ \begin{align} d^{\text{ASY}}_{ij} &= \frac{\text{\# of 0-1 or 1-0 pairs}}{\text{\# of 0-1, 1-0, or 1-1 pairs}}= \frac{2}{3} = 0.67 \end{align} \]
Distance for Qualitative Variables
For categorical variables having \(>2\) levels, a common measure is essentially standardized matching once again.
If \(u\) is the number of variables that match between observations \(i\) and \(j\) and \(p\) is the total number of variables, the measure1 is calculated as: \[d^{\text{CAT}}_{ij} = 1 - \frac{u}{p}\]
Distance for Mixed Variables
But often data has a mix of variable types.
Gower’s distance is a common choice for computing pairwise distances in this case.
The basic idea is to standardize each variable’s contribution to the distance between 0 and 1, and then sum them up.
Gower’s Distance
Gower’s distance (or Gower’s dissimilarity) is calculated as: \[d^{\text{GOW}}_{ij} = \frac{\sum_{k=1}^p \delta_{ijk} d_{ijk}}{\sum_{k=1}^p \delta_{ijk}}\]
where
-
\(\delta_{ijk}\) = 1 if both \(x_{ik}\) and \(x_{jk}\) are non-missing1 (0 otherwise),
- \(d_{ijk}\) depends on variable type
\(d_{ijk}\)
Quantitative numeric \[d_{ijk} = \frac{|x_{ik} - x_{jk}|}{\text{range of variable k}}\]
Qualitative (nominal, categorical) \[d_{ijk} = \begin{cases} 0 \text{ if obs i and j agree on variable k, } \\ 1 \text{ otherwise} \end{cases} \]
Binary \(d_{ijk} = \begin{cases} 0 \text{ if obs i and j are a 1-1 match, } \\ 1 \text{ otherwise} \end{cases}\)
Example of Gower’s Distance1
| Party | Height (cm) | Eye Colour | 2 Terms | From Iowa | |
|---|---|---|---|---|---|
| Biden | Democratic | 182 | Blue | NA | No |
| Trump | Republican | 188 | Blue | No | No |
| Obama | Democratic | 185 | Brown | Yes | No |
| Fillmore | Third Party | 175 | Blue | No | No |
\(\dots\) assume we have this data for all past and present US presidents
Calculations
If we consider 0-0 to be missing we can fill out the \(\delta\) column for Biden (\(i = 1\)) and Trump (\(j = 2\)) as follows:
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | ||
Height |
1 | ||
EyeColour |
1 | ||
2 Terms |
0 | ||
Iowa |
0 |
Party Calculations
| Party | Height (cm) | Eye Colour | 2 Terms | From Iowa | |
|---|---|---|---|---|---|
| Biden | Democratic | 182 | Blue | NA | No |
| Trump | Republican | 188 | Blue | No | No |
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | 1 | 1 |
Height |
1 | ||
EyeColour |
1 | ||
2 Terms |
0 | ||
Iowa |
0 |
Height Calculations
To calculate \(d_{12k}\) we need to know the range of the qualitative variable Height(cm)
- Tallest President: Abraham Lincoln at 193 centimeters
- Shortest President: James Madison at 163 centimeters
Range of variable \(k = 2\) is 193-163 = 30
\(d_{1,2,2} = \dfrac{|x_{ik} - x_{jk}|}{\text{range of variable k}} = \dfrac{|188 - 185|}{30} = 0.1\)
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | 1 | 1 |
Height |
1 | 0.1 | 0.1 |
EyeColour |
1 | ||
2 Terms |
0 | ||
Iowa |
0 |
EyeColour Calculations
| Party | Height (cm) | Eye Colour | 2 Terms | From Iowa | |
|---|---|---|---|---|---|
| Biden | Democratic | 182 | Blue | NA | No |
| Trump | Republican | 188 | Blue | No | No |
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | 1 | 1 |
Height |
1 | 0.1 | 0.1 |
EyeColour |
1 | 0 | 0 |
2 Terms |
0 | ||
Iowa |
0 |
2 Terms Calculations
| Party | Height (cm) | Eye Colour | 2 Terms | From Iowa | |
|---|---|---|---|---|---|
| Biden | Democratic | 182 | Blue | NA | No |
| Trump | Republican | 188 | Blue | No | No |
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | 1 | 1 |
Height |
1 | 0.1 | 0.1 |
EyeColour |
1 | 0 | 0 |
2 Terms |
0 | - | 0 |
Iowa |
0 |
From Iowa Calculations
| Party | Height (cm) | Eye Colour | 2 Terms | From Iowa | |
|---|---|---|---|---|---|
| Biden | Democratic | 182 | Blue | NA | No |
| Trump | Republican | 188 | Blue | No | No |
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | 1 | 1 |
Height |
1 | 0.1 | 0.1 |
EyeColour |
1 | 0 | 0 |
2 Terms |
0 | - | 0 |
Iowa |
0 | 0 | 0 |
Gower’s Distance Calculation
| \(k\) | \(\delta_{12k}\) | \(d_{12k}\) | \(\delta_{12k}d_{12k}\) |
|---|---|---|---|
Party |
1 | 1 | 1 |
Height |
1 | 0.1 | 0.1 |
EyeColour |
1 | 0 | 0 |
2 Terms |
0 | - | 0 |
Iowa |
0 | 0 | 0 |
| Total | 3 | 1.1 |
\[ d^{\text{GOW}}_{ij} = \frac{\sum_{k=1}^p \delta_{ijk} d_{ijk}}{\sum_{k=1}^p \delta_{ijk}} = \frac{1.1}{3} = 0.3666667 \]
Comments
Gower distance will always be between 0.0 and 1.0
a distance of 0.0 means the two observations are identical for all non-missing predictors
a distance of 1.0 means the two observations are as far apart as possible for that data set
The Gower distance can be used with purely numeric or purely non-numeric data, but for such scenarios there are better distance metrics available.
There are several variations of the Gower distance, so if you encounter it, you should read the documentation carefully.